Lecture 21

Introduction to Time Series Data in R

Learning Objectives

By the end of this lecture, you should be able to:

Understand what time series data is and why it’s useful
Work with date and time objects in R
Load and visualize time series data in R
Apply basic time series operations: decomposition, smoothing, and forecasting
Use ts, zoo, and xts objects for time-indexed data
Understand tidy approaches using tsibble and feasts
Recognize real-world environmental science applications of time series

What is Time Series Data?

Time series data is a collection of observations recorded sequentially over time. Unlike other data types, time series data is ordered, and that order carries critical information.

Examples:

Streamflow measurements (e.g., daily CFS at a USGS gage)
Atmospheric CO₂ levels (e.g., Mauna Loa Observatory)
Snowpack depth over time
Urban water consumption by month

Why Time Series Matter

Time series analysis helps us:

Understand trends and patterns
Detect anomalies (e.g., droughts, sensor failures)
Forecast future values (e.g., streamflow, temperature)

Working with Date Objects in R

Time series analysis depends on accurate and well-formatted date/time information.
Before we can analyis time series data, we need to understand how R handles dates and times.
R has built-in classes for date and time objects, which are essential for time series analysis.

Base R Date Functions

R has several native classes for handling dates and times:

Date: Date object

as.Date("2024-04-08")
#> [1] "2024-04-08"

POSIXct: Date and time

as.POSIXct("2024-04-08 14:30:00")
#> [1] "2024-04-08 14:30:00 MDT"

POSIXlt: List of date and time components

(lt <- as.POSIXlt("2024-04-08 14:30:00"))
#> [1] "2024-04-08 14:30:00 MDT"

lt$hour
#> [1] 14

Date Sequences

You can create sequences of dates using the seq.Date() function:

from: Start date
to: End date (optional)
by: Interval (e.g., “day”, “month”, “year”)
length.out: Number of dates to generate

seq.Date(from = as.Date("2024-01-01"), by = "month", length.out = 12)
#>  [1] "2024-01-01" "2024-02-01" "2024-03-01" "2024-04-01" "2024-05-01"
#>  [6] "2024-06-01" "2024-07-01" "2024-08-01" "2024-09-01" "2024-10-01"
#> [11] "2024-11-01" "2024-12-01"

You can also use seq() to create sequences of POSIXct/lt objects:

from: Start date/time
to: End date/time (optional)
by: Interval (e.g., “hour”, “minute”, “second”)
length.out: Number of dates to generate

seq(from = as.POSIXct("2024-01-01 00:00"), 
    to = as.POSIXct("2024-01-02 00:00"), 
    by = "hour")
#>  [1] "2024-01-01 00:00:00 MST" "2024-01-01 01:00:00 MST"
#>  [3] "2024-01-01 02:00:00 MST" "2024-01-01 03:00:00 MST"
#>  [5] "2024-01-01 04:00:00 MST" "2024-01-01 05:00:00 MST"
#>  [7] "2024-01-01 06:00:00 MST" "2024-01-01 07:00:00 MST"
#>  [9] "2024-01-01 08:00:00 MST" "2024-01-01 09:00:00 MST"
#> [11] "2024-01-01 10:00:00 MST" "2024-01-01 11:00:00 MST"
#> [13] "2024-01-01 12:00:00 MST" "2024-01-01 13:00:00 MST"
#> [15] "2024-01-01 14:00:00 MST" "2024-01-01 15:00:00 MST"
#> [17] "2024-01-01 16:00:00 MST" "2024-01-01 17:00:00 MST"
#> [19] "2024-01-01 18:00:00 MST" "2024-01-01 19:00:00 MST"
#> [21] "2024-01-01 20:00:00 MST" "2024-01-01 21:00:00 MST"
#> [23] "2024-01-01 22:00:00 MST" "2024-01-01 23:00:00 MST"
#> [25] "2024-01-02 00:00:00 MST"

Timezones

By default, R uses the system’s timezone.
The Sys.timezone() function returns the current timezone.
If you want to use anthor timezone, say GMT/UTC, you can change it:

Sys.timezone()
#> [1] "America/Denver"

as.POSIXct("2024-04-08 14:30:00", tz = "GMT")
#> [1] "2024-04-08 14:30:00 GMT"

(obj = as.POSIXct("2024-04-08 14:30:00"))
#> [1] "2024-04-08 14:30:00 MDT"

format(obj, tz = "EST")
#> [1] "2024-04-08 15:30:00"

lubridate Package

The lubridate package comes with the tidyverse and is designed to make working with dates and times easier.
It provides a consistent set of functions for parsing, manipulating, and formatting date-time objects.

library(lubridate)
ymd("20240408")        # Parse date
#> [1] "2024-04-08"
ymd_hms("20240408 123000")
#> [1] "2024-04-08 12:30:00 UTC"

now()                  # Current date and time
#> [1] "2025-04-14 09:28:58 MDT"
date <- ymd("2023-12-01")
month(date)           # Extract month
#> [1] 12
day(date)
#> [1] 1
week(date)
#> [1] 48

Use lubridate to handle inconsistent formats and to align data with time zones, daylight savings, etc.

lubridate timezones

lubridate also provides functions for working with time zones. You can convert between time zones using with_tz() and force_tz().

(date <- ymd_hms("2024-04-08 14:30:00", tz = "America/New_York"))
#> [1] "2024-04-08 14:30:00 EDT"

# Change time zone without changing time
force_tz(date, "America/Los_Angeles")  
#> [1] "2024-04-08 14:30:00 PDT"

# Convert to another timezone
with_tz(date, "America/Los_Angeles")  
#> [1] "2024-04-08 11:30:00 PDT"

R Packages for Time Series

R has several packages/systme for time series analysis, including:

ts: Base R time series class
zoo: Provides a flexible class for ordered observations
xts: Extensible time series class for irregularly spaced data
forecast: Functions for forecasting time series data
tsibble: Tidy time series data frames
feasts: Functions for time series analysis and visualization
modeltime: Time series modeling with tidymodels

library(tidyverse)
library(zoo)
library(tsibble)
library(feasts)

When to Use Which Time Series Format?

Format	Best For	Advantages	Limitations
`ts`	Regular, simple time series	Built into base R, supported by `forecast`	Rigid time format, inflexible for joins
`zoo`	Irregular time steps	Arbitrary index, supports irregular data	More complex syntax
`xts`	Financial-style or irregular data	Good for date-time indexing and joins	More complex to visualize
`tsibble`	Tidyverse workflows	Pipes with `dplyr`, `ggplot2`, forecasting with `fable`	Requires `tsibble` structure
`tibble` + `Date`	General purpose	Flexible, tidy	Needs conversion for time series modeling

Key Concepts in Time Series

1. Trend: Long-term increase or decrease in the data
2. Seasonality: Repeating short-term cycle (e.g., annual snowmelt)
3. Noise: Random variation
4. Stationarity: Statistical properties (mean, variance) don’t change over time
5. Autocorrelation: Correlation of a time series with its own past values

Introducing the Mauna Loa CO₂ Dataset

Mauna Loa CO₂ Dataset

The co2 dataset is a classic example of time series data. It contains monthly atmospheric CO₂ concentrations measured at the Mauna Loa Observatory in Hawaii.
co2 is a built-in dataset representing monthly CO₂ concentrations from 1959 onward.

class(co2)
#> [1] "ts"
co2
#>         Jan    Feb    Mar    Apr    May    Jun    Jul    Aug    Sep    Oct
#> 1959 315.42 316.31 316.50 317.56 318.13 318.00 316.39 314.65 313.68 313.18
#> 1960 316.27 316.81 317.42 318.87 319.87 319.43 318.01 315.74 314.00 313.68
#> 1961 316.73 317.54 318.38 319.31 320.42 319.61 318.42 316.63 314.83 315.16
#> 1962 317.78 318.40 319.53 320.42 320.85 320.45 319.45 317.25 316.11 315.27
#> 1963 318.58 318.92 319.70 321.22 322.08 321.31 319.58 317.61 316.05 315.83
#> 1964 319.41 320.07 320.74 321.40 322.06 321.73 320.27 318.54 316.54 316.71
#> 1965 319.27 320.28 320.73 321.97 322.00 321.71 321.05 318.71 317.66 317.14
#> 1966 320.46 321.43 322.23 323.54 323.91 323.59 322.24 320.20 318.48 317.94
#> 1967 322.17 322.34 322.88 324.25 324.83 323.93 322.38 320.76 319.10 319.24
#> 1968 322.40 322.99 323.73 324.86 325.40 325.20 323.98 321.95 320.18 320.09
#> 1969 323.83 324.26 325.47 326.50 327.21 326.54 325.72 323.50 322.22 321.62
#> 1970 324.89 325.82 326.77 327.97 327.91 327.50 326.18 324.53 322.93 322.90
#> 1971 326.01 326.51 327.01 327.62 328.76 328.40 327.20 325.27 323.20 323.40
#> 1972 326.60 327.47 327.58 329.56 329.90 328.92 327.88 326.16 324.68 325.04
#> 1973 328.37 329.40 330.14 331.33 332.31 331.90 330.70 329.15 327.35 327.02
#> 1974 329.18 330.55 331.32 332.48 332.92 332.08 331.01 329.23 327.27 327.21
#> 1975 330.23 331.25 331.87 333.14 333.80 333.43 331.73 329.90 328.40 328.17
#> 1976 331.58 332.39 333.33 334.41 334.71 334.17 332.89 330.77 329.14 328.78
#> 1977 332.75 333.24 334.53 335.90 336.57 336.10 334.76 332.59 331.42 330.98
#> 1978 334.80 335.22 336.47 337.59 337.84 337.72 336.37 334.51 332.60 332.38
#> 1979 336.05 336.59 337.79 338.71 339.30 339.12 337.56 335.92 333.75 333.70
#> 1980 337.84 338.19 339.91 340.60 341.29 341.00 339.39 337.43 335.72 335.84
#> 1981 339.06 340.30 341.21 342.33 342.74 342.08 340.32 338.26 336.52 336.68
#> 1982 340.57 341.44 342.53 343.39 343.96 343.18 341.88 339.65 337.81 337.69
#> 1983 341.20 342.35 342.93 344.77 345.58 345.14 343.81 342.21 339.69 339.82
#> 1984 343.52 344.33 345.11 346.88 347.25 346.62 345.22 343.11 340.90 341.18
#> 1985 344.79 345.82 347.25 348.17 348.74 348.07 346.38 344.51 342.92 342.62
#> 1986 346.11 346.78 347.68 349.37 350.03 349.37 347.76 345.73 344.68 343.99
#> 1987 347.84 348.29 349.23 350.80 351.66 351.07 349.33 347.92 346.27 346.18
#> 1988 350.25 351.54 352.05 353.41 354.04 353.62 352.22 350.27 348.55 348.72
#> 1989 352.60 352.92 353.53 355.26 355.52 354.97 353.75 351.52 349.64 349.83
#> 1990 353.50 354.55 355.23 356.04 357.00 356.07 354.67 352.76 350.82 351.04
#> 1991 354.59 355.63 357.03 358.48 359.22 358.12 356.06 353.92 352.05 352.11
#> 1992 355.88 356.63 357.72 359.07 359.58 359.17 356.94 354.92 352.94 353.23
#> 1993 356.63 357.10 358.32 359.41 360.23 359.55 357.53 355.48 353.67 353.95
#> 1994 358.34 358.89 359.95 361.25 361.67 360.94 359.55 357.49 355.84 356.00
#> 1995 359.98 361.03 361.66 363.48 363.82 363.30 361.94 359.50 358.11 357.80
#> 1996 362.09 363.29 364.06 364.76 365.45 365.01 363.70 361.54 359.51 359.65
#> 1997 363.23 364.06 364.61 366.40 366.84 365.68 364.52 362.57 360.24 360.83
#>         Nov    Dec
#> 1959 314.66 315.43
#> 1960 314.84 316.03
#> 1961 315.94 316.85
#> 1962 316.53 317.53
#> 1963 316.91 318.20
#> 1964 317.53 318.55
#> 1965 318.70 319.25
#> 1966 319.63 320.87
#> 1967 320.56 321.80
#> 1968 321.16 322.74
#> 1969 322.69 323.95
#> 1970 323.85 324.96
#> 1971 324.63 325.85
#> 1972 326.34 327.39
#> 1973 327.99 328.48
#> 1974 328.29 329.41
#> 1975 329.32 330.59
#> 1976 330.14 331.52
#> 1977 332.24 333.68
#> 1978 333.75 334.78
#> 1979 335.12 336.56
#> 1980 336.93 338.04
#> 1981 338.19 339.44
#> 1982 339.09 340.32
#> 1983 340.98 342.82
#> 1984 342.80 344.04
#> 1985 344.06 345.38
#> 1986 345.48 346.72
#> 1987 347.64 348.78
#> 1988 349.91 351.18
#> 1989 351.14 352.37
#> 1990 352.69 354.07
#> 1991 353.64 354.89
#> 1992 354.09 355.33
#> 1993 355.30 356.78
#> 1994 357.59 359.05
#> 1995 359.61 360.74
#> 1996 360.80 362.38
#> 1997 362.49 364.34

Initial Plot

The co2 dataset is a time series object (ts) with 12 observations per year, starting from January 1959.
There is a default plot method for ts objects that we can take advantage of:

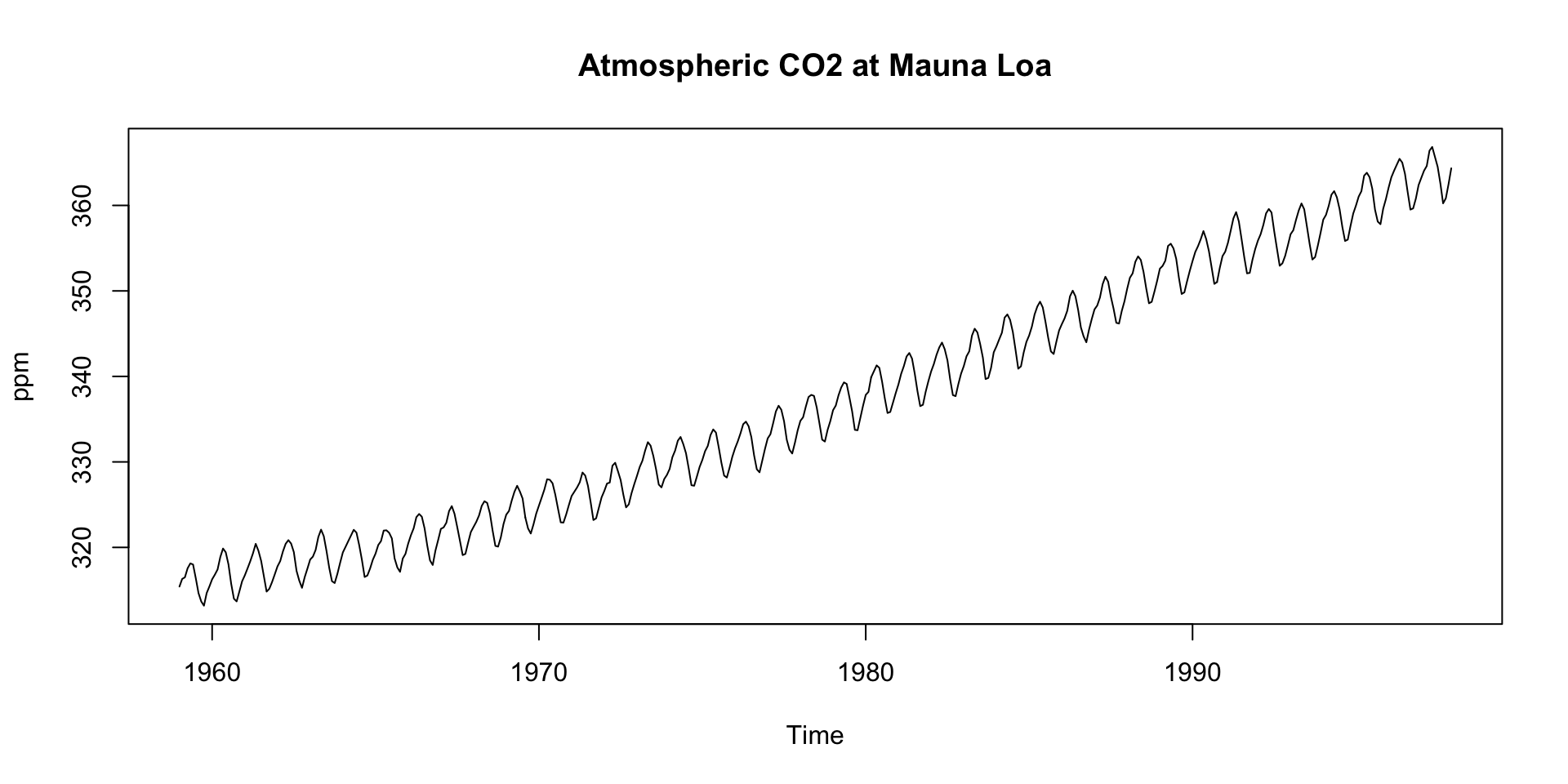
plot(co2, main = "Atmospheric CO2 at Mauna Loa", ylab = "ppm")

We see:

An upward trend
Regular seasonal oscillations (higher in winter, lower in summer)

Understanding `ts` Objects

You can think of ts objects as numeric vectors with time attributes.

ts objects are used to represent time series data and are created using the ts() function.
They have attributes like start, end, and frequency that define the time index.
start and end define the time range of the data.
frequency defines the number of observations per unit of time (e.g., 12 for monthly data).

class(co2)    
#> [1] "ts"
start(co2)    
#> [1] 1959    1
end(co2)      
#> [1] 1997   12
frequency(co2)
#> [1] 12

Subsetting and Plotting

Like vectors, you can subset ts objects using indexing.
For example, to extract the first year of data:

co2[1:12]  # First year
#>  [1] 315.42 316.31 316.50 317.56 318.13 318.00 316.39 314.65 313.68 313.18
#> [11] 314.66 315.43

Or, a specific range of years:

window(co2, start = c(1990, 1), end = c(1995, 12))
#>         Jan    Feb    Mar    Apr    May    Jun    Jul    Aug    Sep    Oct
#> 1990 353.50 354.55 355.23 356.04 357.00 356.07 354.67 352.76 350.82 351.04
#> 1991 354.59 355.63 357.03 358.48 359.22 358.12 356.06 353.92 352.05 352.11
#> 1992 355.88 356.63 357.72 359.07 359.58 359.17 356.94 354.92 352.94 353.23
#> 1993 356.63 357.10 358.32 359.41 360.23 359.55 357.53 355.48 353.67 353.95
#> 1994 358.34 358.89 359.95 361.25 361.67 360.94 359.55 357.49 355.84 356.00
#> 1995 359.98 361.03 361.66 363.48 363.82 363.30 361.94 359.50 358.11 357.80
#>         Nov    Dec
#> 1990 352.69 354.07
#> 1991 353.64 354.89
#> 1992 354.09 355.33
#> 1993 355.30 356.78
#> 1994 357.59 359.05
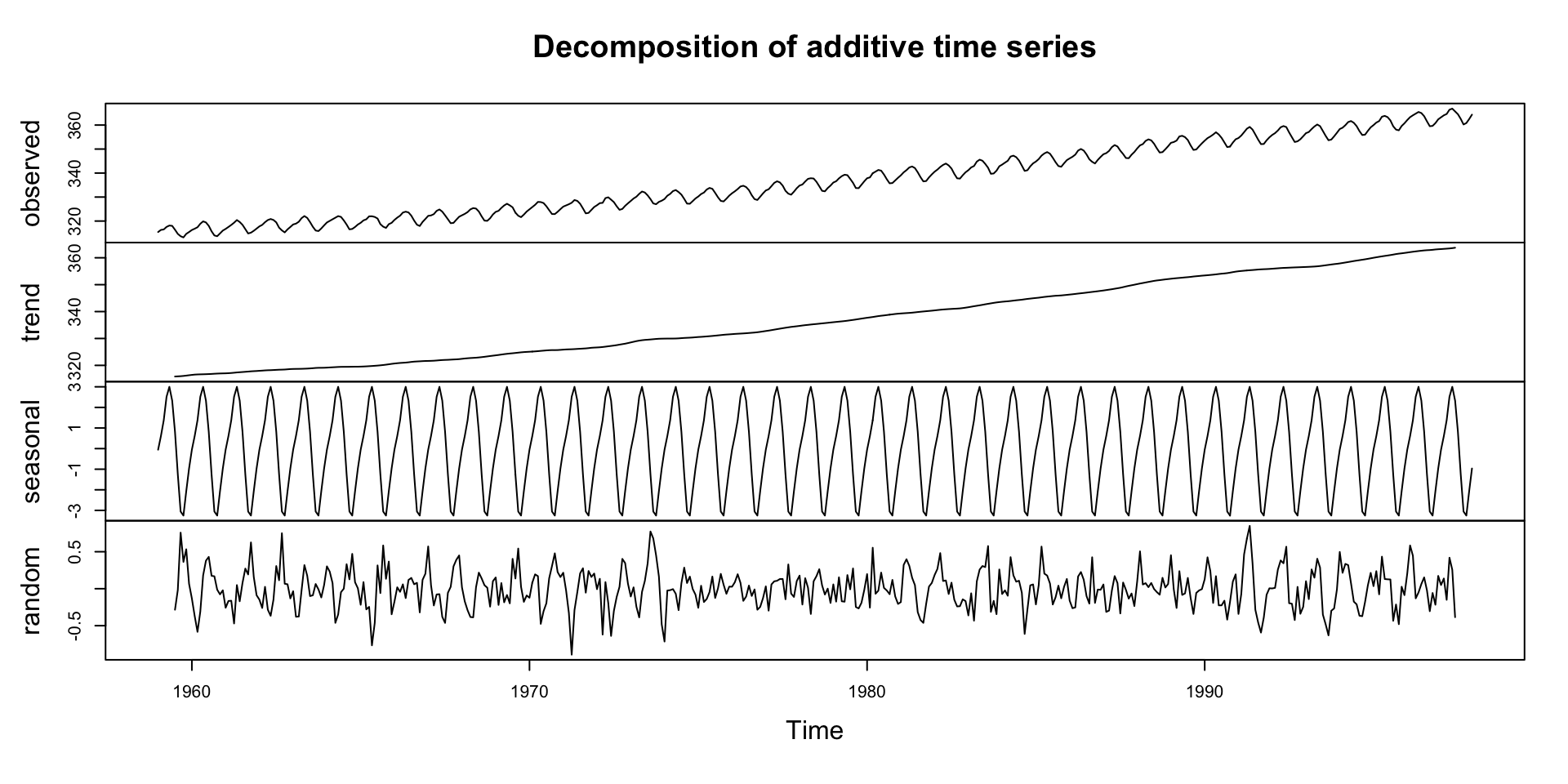
#> 1995 359.61 360.74

Decomposing a Time Series

Decomposition is a technique to separate a time series into its components: trend, seasonality, and residuals.
This helps separate structure from noise.
In environmental science, this is useful for:
Removing seasonality to study droughts
Analyzing long-term trends
Understanding seasonal patterns in streamflow
Identifying anomalies in water quality data
Detecting changes in vegetation phenology
Monitoring seasonal patterns in temperature
Analyzing seasonal patterns in water demand
…

What is Decomposition?

Decomposition separates a time series into interpretable components:

Trend: Long-term movement
Seasonality: Regular, periodic fluctuations
Residual/Irregular: Random noise or anomalies

Additive vs Multiplicative

Additive model:
\[ Y_t = T_t + S_t + R_t \]
Multiplicative model:
\[ Y_t = T_t \times S_t \times R_t \]

Use additive if seasonal variation is roughly constant.
Use multiplicative if it grows/shrinks with the trend.

Example

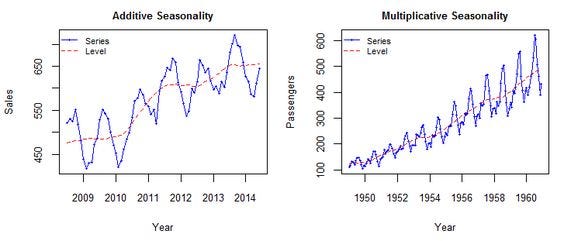
Why Decompose?

Trend: Are CO₂ levels increasing?
Seasonality: Are there predictable cycles each year?
Remainder: What’s left after we remove trend and season? (what is the randomness?)

Decompostion in R

The decompose() function in R can be used to perform this operation.
The decompose() function by default assumes that the time series is additive

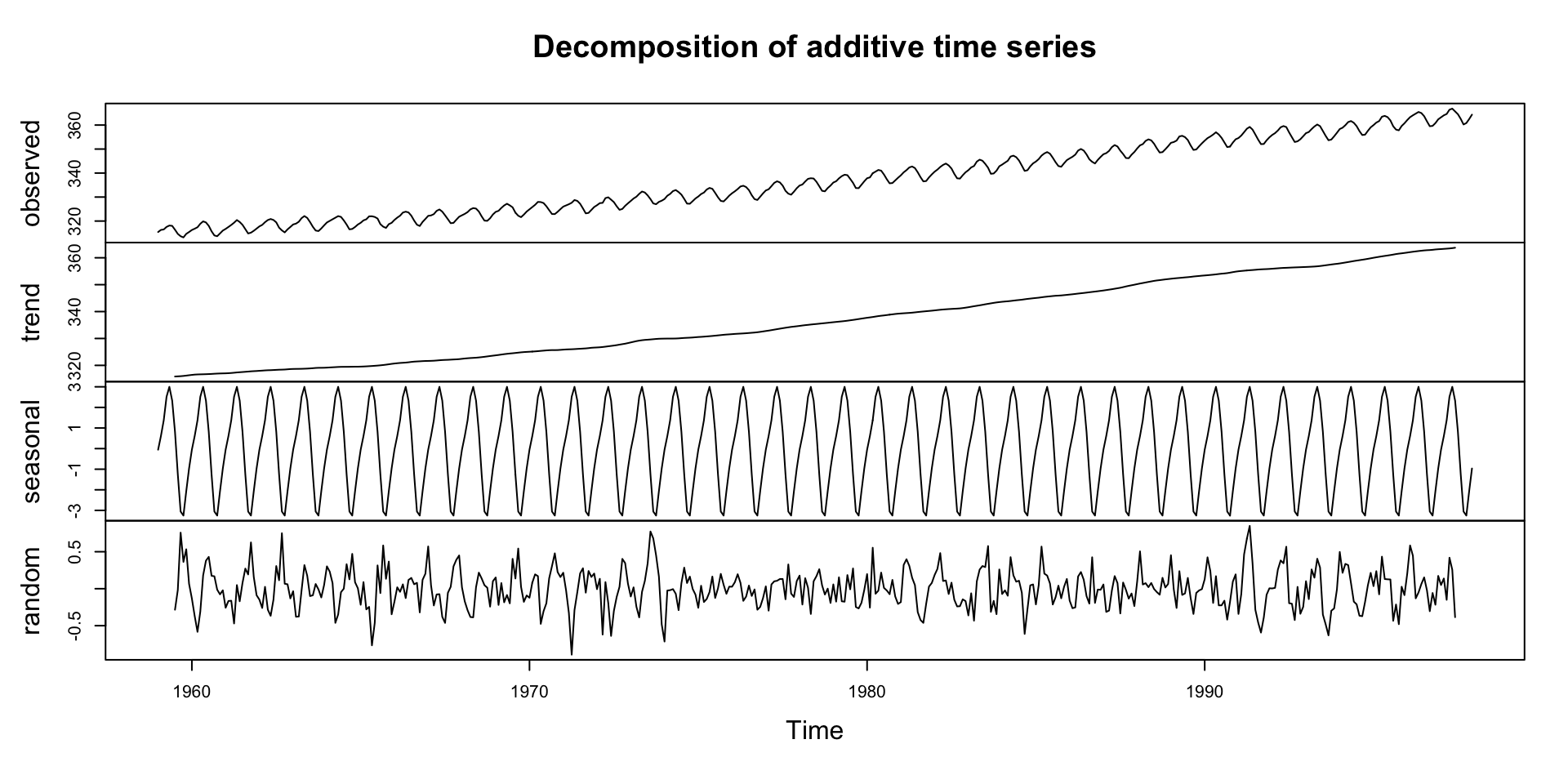
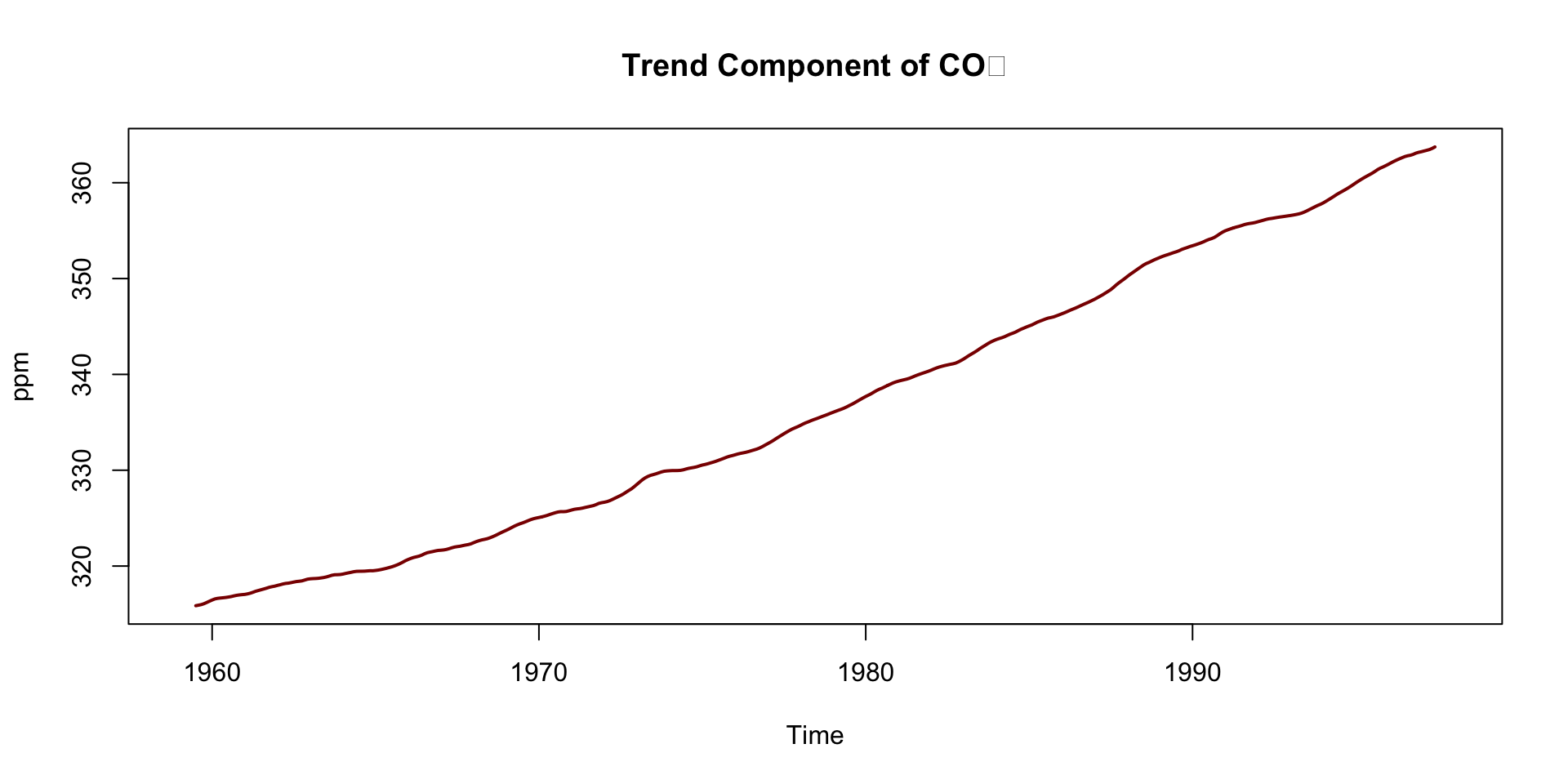
decomp = decompose(co2, type = "additive")
plot(decomp)

Deep Dive: Trend Component

plot(decomp$trend, main = "Trend Component of CO₂", ylab = "ppm", col = "darkred", lwd = 2)

Steady upward slope from ~316 ppm in 1959 to ~365 ppm in the late 1990s
Captures the long-term forcing from human activity:
- Fossil fuel combustion
- Deforestation
This trend underpins climate change science — known as the Keeling Curve
Notice how the trend smooths short-term fluctuations

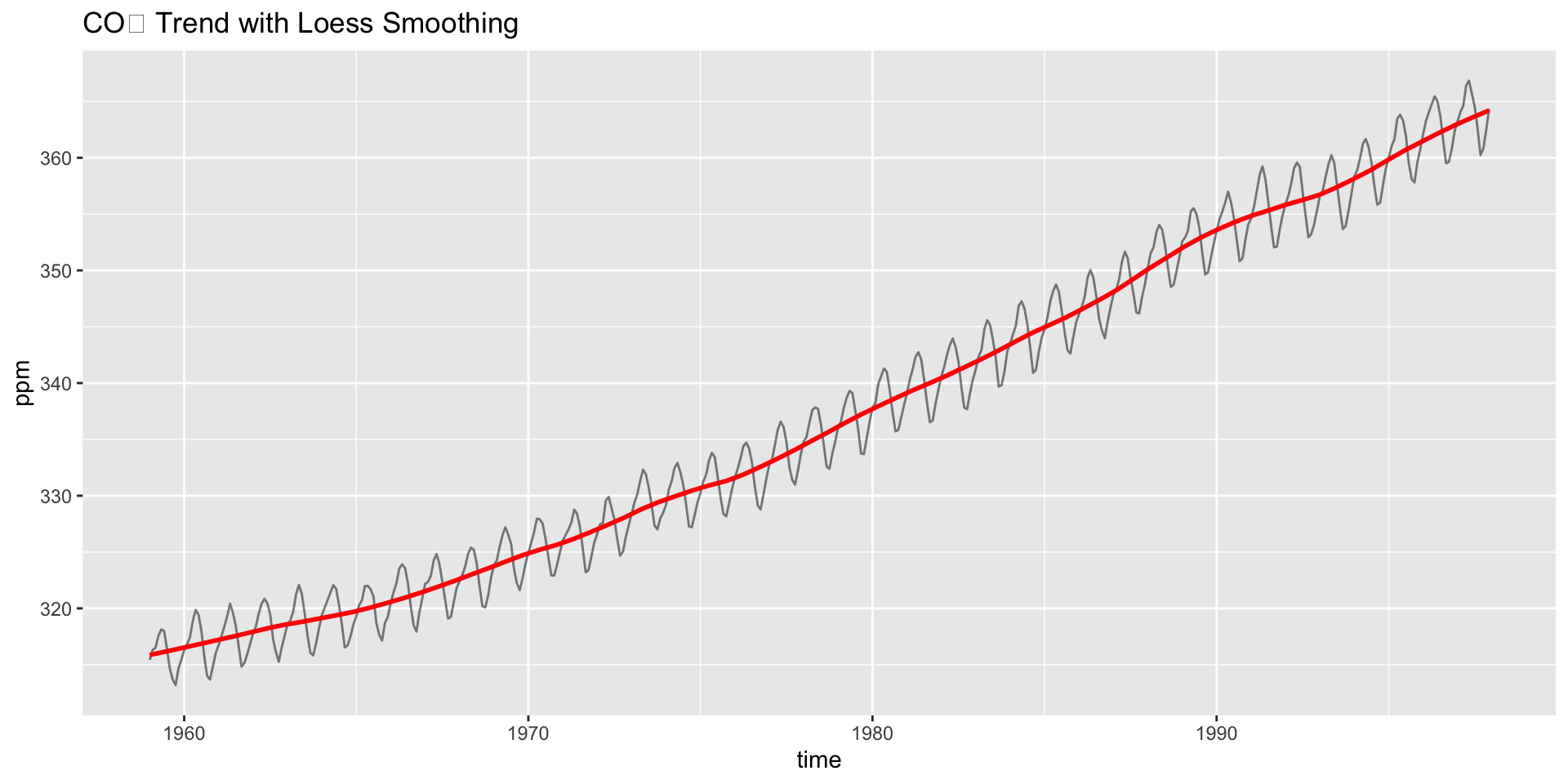
Interpreting the Trend

A linear model or loess smoother can also help quantify the trend:

co2_df <- data.frame(time = time(co2), co2 = as.numeric(co2))

lm(as.numeric(co2) ~ time(co2)) |> 
  summary()
#> 
#> Call:
#> lm(formula = as.numeric(co2) ~ time(co2))
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -6.0399 -1.9476 -0.0017  1.9113  6.5149 
#> 
#> Coefficients:
#>               Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -2.250e+03  2.127e+01  -105.8   <2e-16 ***
#> time(co2)    1.308e+00  1.075e-02   121.6   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 2.618 on 466 degrees of freedom
#> Multiple R-squared:  0.9695, Adjusted R-squared:  0.9694 
#> F-statistic: 1.479e+04 on 1 and 466 DF,  p-value: < 2.2e-16

co2_df |>
  ggplot(aes(x = time, y = co2)) +
  geom_line(alpha = 0.5) +
  geom_smooth(method = "loess", span = 0.2, color = "red", se = FALSE) +
  labs(title = "CO₂ Trend with Loess Smoothing", y = "ppm")

Do you see acceleration in the rise over time?

De-Trending

Detrending is the process of removing the trend component from a time series.
This can help for modeling the trend + residual only:

deseasonalized <- co2 - decomp$trend
plot(deseasonalized, main = "De-trended Series")

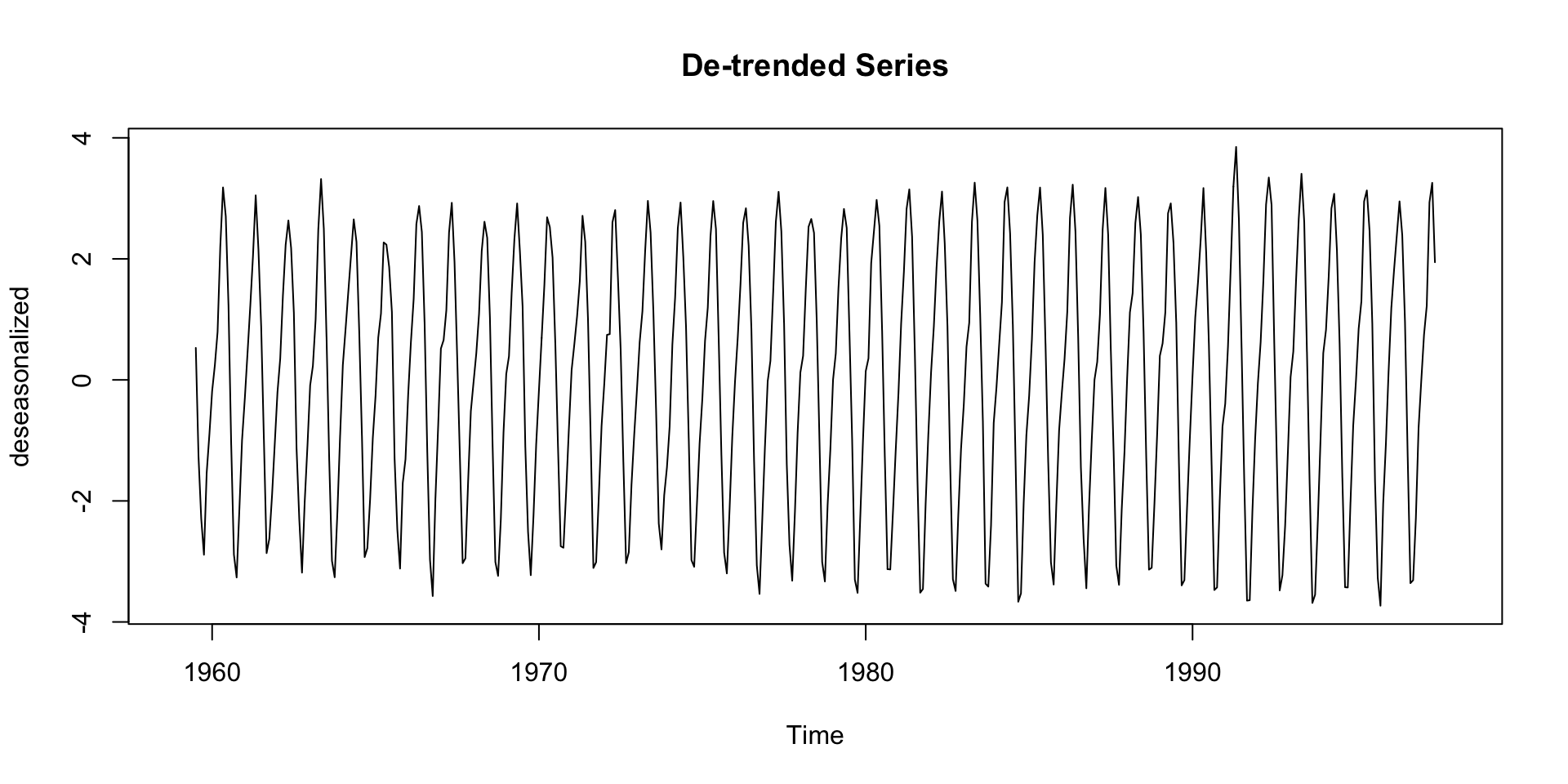
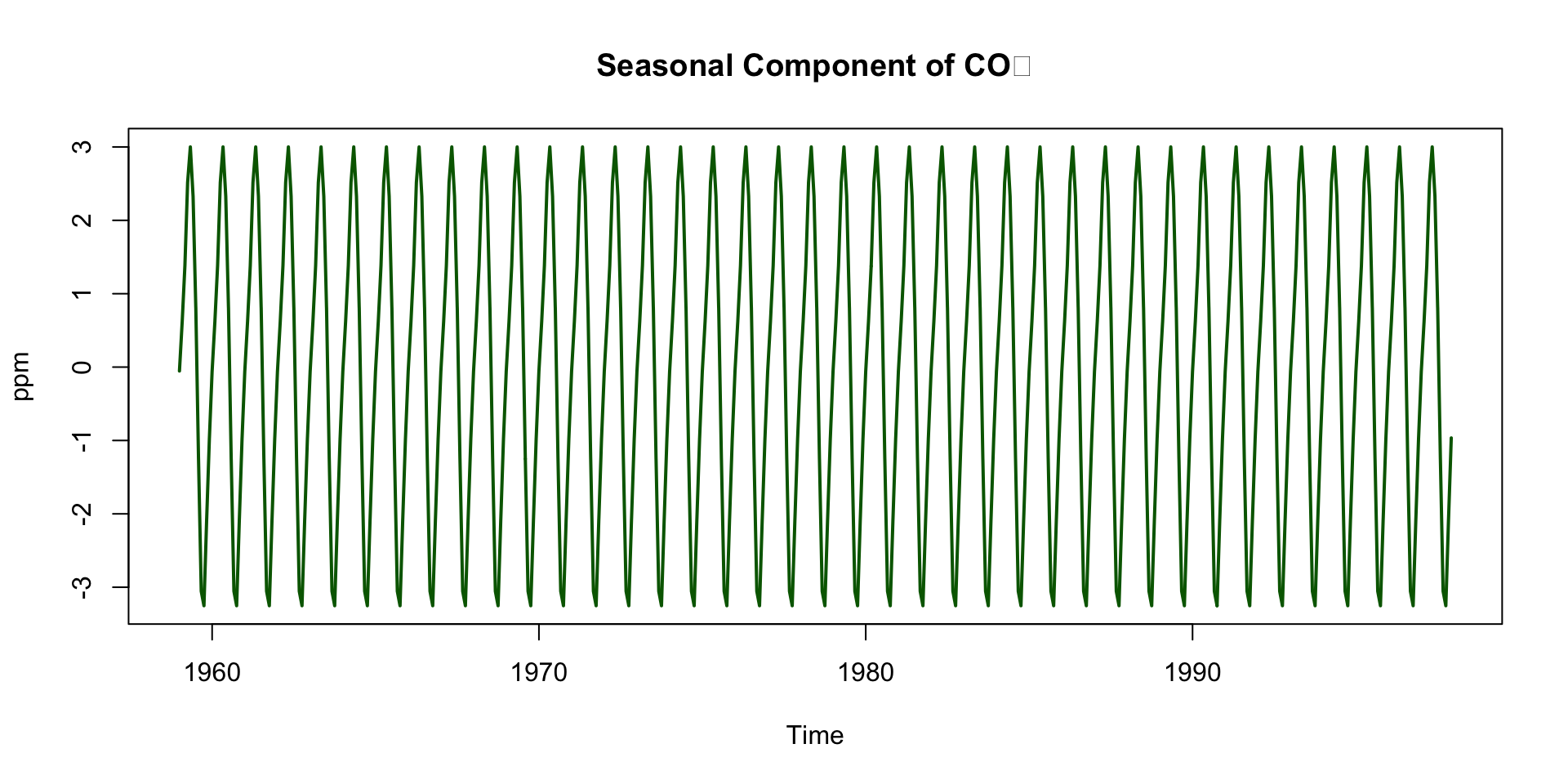
Deep Dive: Seasonal Component

plot(decomp$seasonal, main = "Seasonal Component of CO₂", 
     ylab = "ppm", col = "darkgreen", lwd = 2)

Repeats every 12 months
Peaks around May, drops in September–October
Driven by biospheric fluxes:
- Photosynthesis during spring/summer → CO₂ drawdown
- Decomposition and respiration in winter → CO₂ release
Seasonal Cycle is Northern Hemisphere-Dominated (Mauna Loa is in the Northern Hemisphere)
Northern Hemisphere contains more landmass and vegetation
So its biosphere exerts a stronger influence on global CO₂ than the Southern Hemisphere
This explains the pronounced seasonal cycle in the signal

De-seasonalizing

This can help for modeling the seasonal + residual only:

deseasonalized <- co2 - decomp$seasonal
plot(deseasonalized, main = "De-seasonalized Series")

Deep Dive: Remainder Component

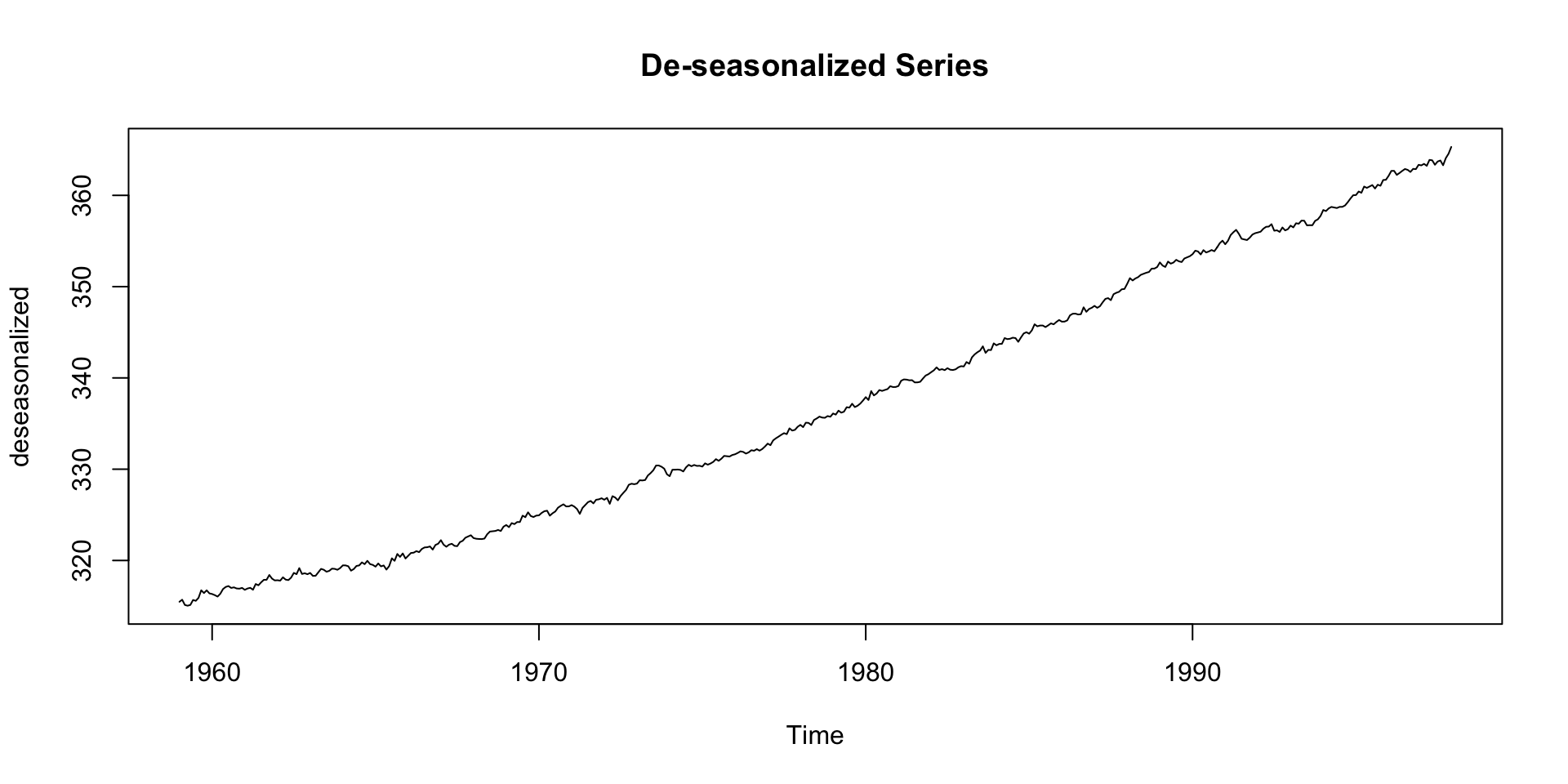
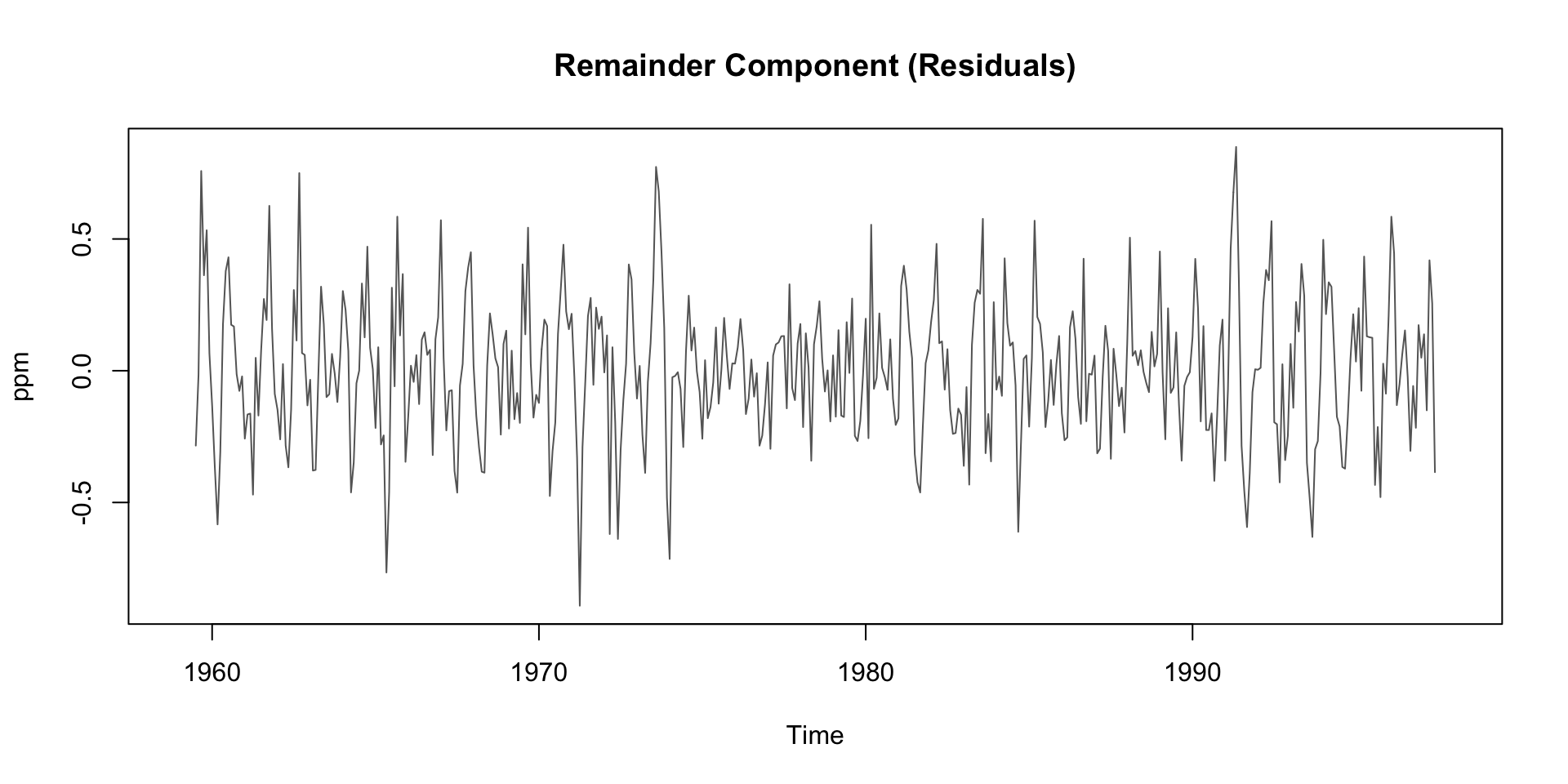
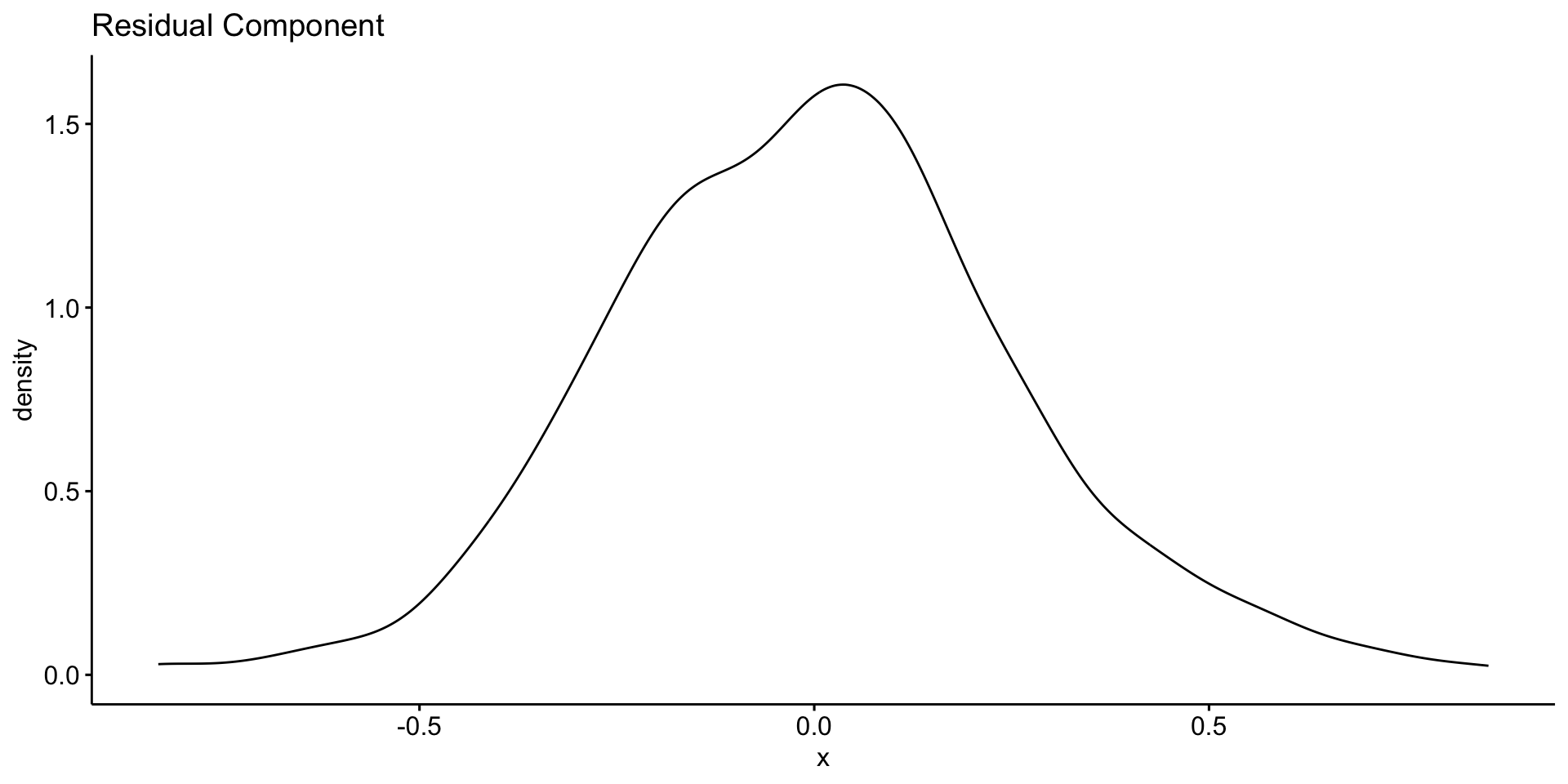
plot(decomp$random, main = "Remainder Component (Residuals)", 
     ylab = "ppm", col = "gray40", lwd = 1)

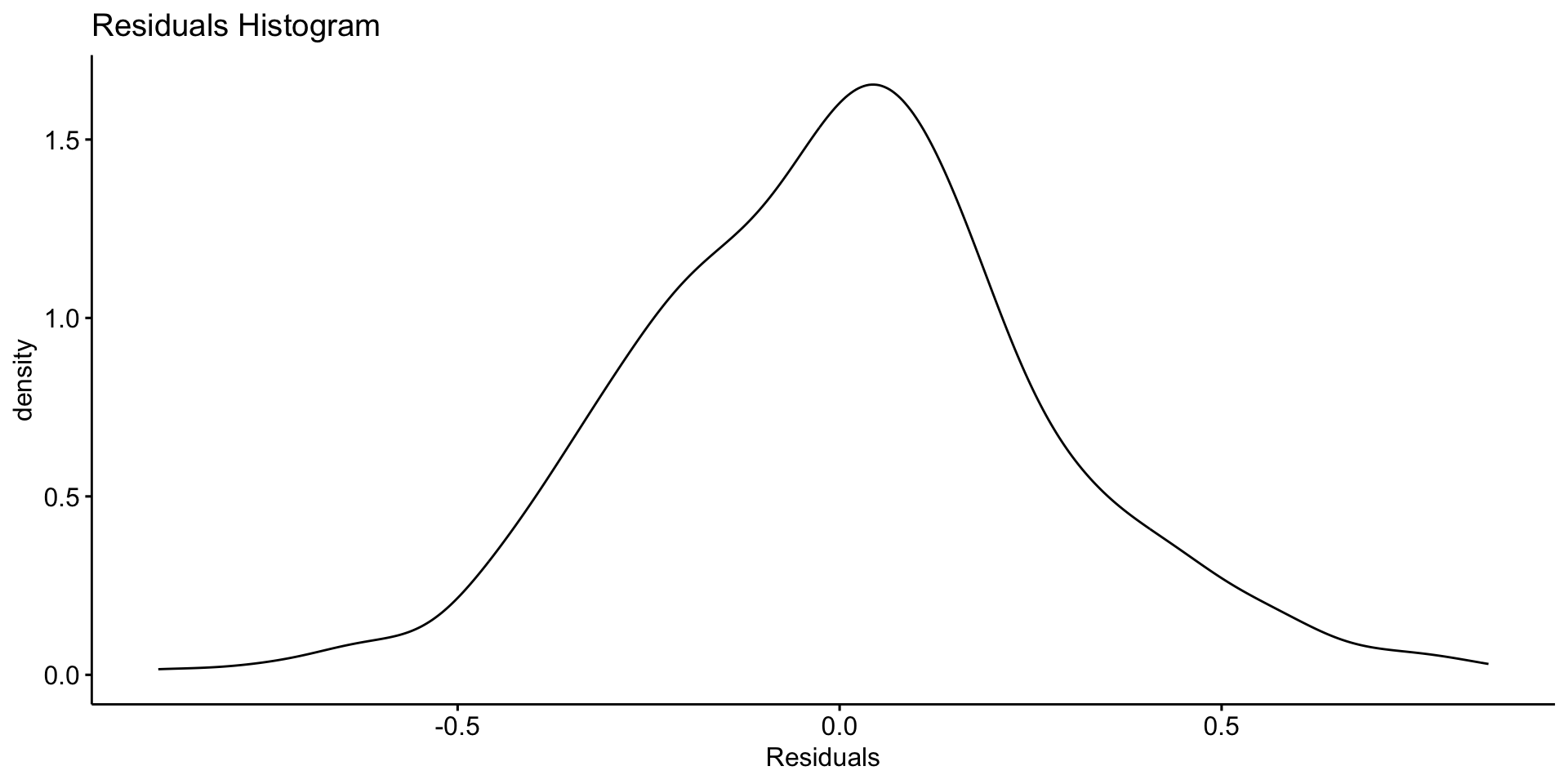
Residuals are the “leftover” part of the time series after removing trend and seasonality
Contains irregular, short-term fluctuations
Can be used to identify anomalies or outliers
Important for understanding noise in the data
Possible sources:
- Volcanic activity (e.g. El Chichón, Mt. Pinatubo)
- Measurement error
- El Niño/La Niña events (which affect carbon flux)
Typically small amplitude: ±0.2 ppm

Asssessing Patterns in Error?

You might compute the standard deviation of the residuals to assess noise:

sd(na.omit(decomp$random))
#> [1] 0.2651064

Or evaluate the residules like we did for Linear Modeling!

ggpubr::ggdensity(decomp$random, main = "Residuals Histogram", xlab = "Residuals")

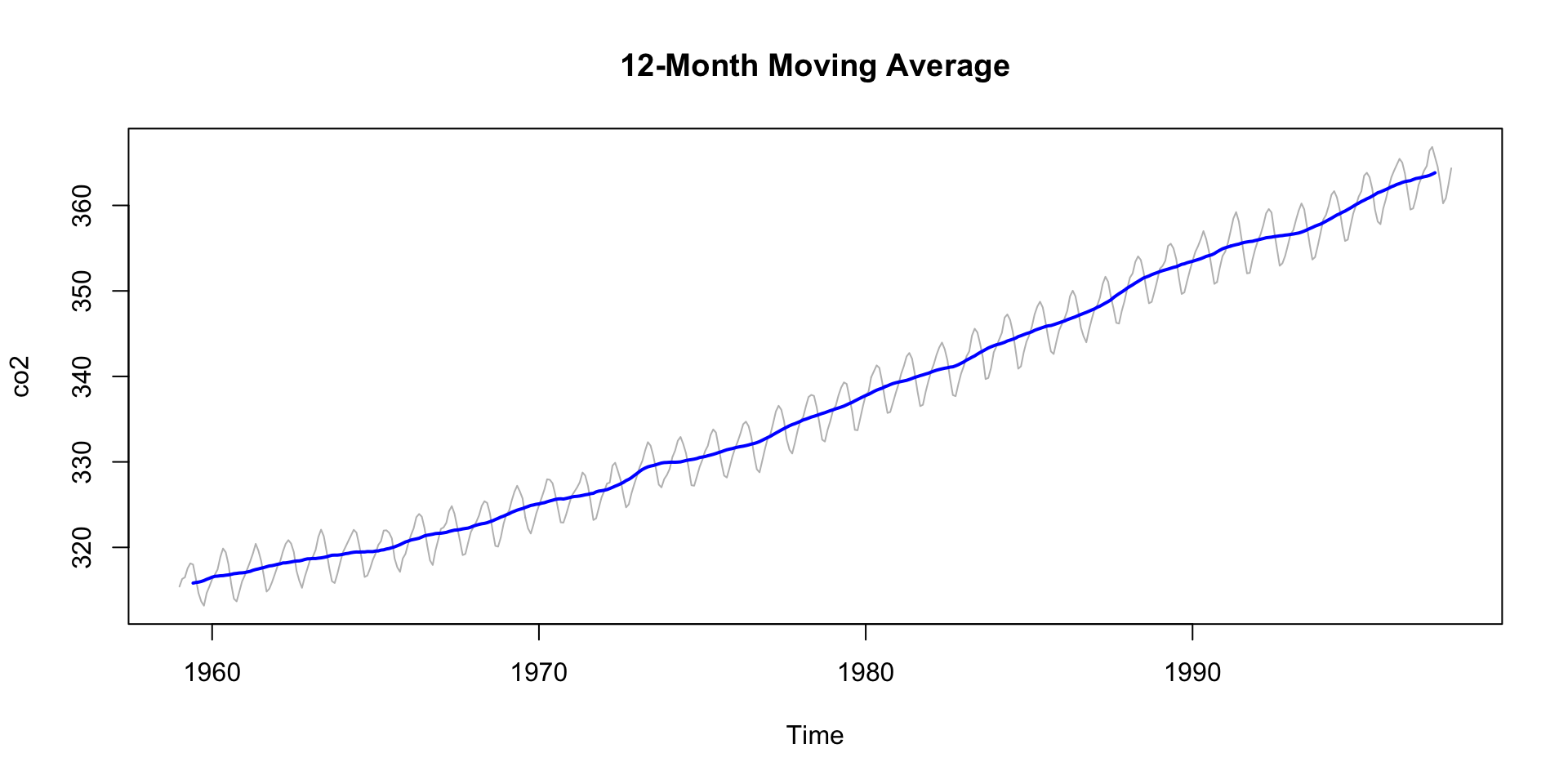
Smoothing to Remove Noise

If your data is noisy - and without usefull pattern - you can use a moving average to smooth it out.

The zoo package provides a convenient function for this that we have already seen in the COVID lab.
The rollmean() function from the zoo package is useful for this.
The k parameter specifies the window size for the moving average.
The align parameter specifies how to align the moving average with the original data (e.g., “center”, “left”, “right”).
The na.pad parameter specifies whether to pad the result with NA values.

co2_smooth <- zoo::rollmean(co2, k = 12, align = "center", na.pad = TRUE)

plot(co2, col = "grey", main = "12-Month Moving Average")
lines(co2_smooth, col = "blue", lwd = 2)

STL Decomposition (Loess-based)

STL (Seasonal-Trend decomposition using Loess) adapts to changing trend or seasonality over time
Doesn’t assume constant seasonal effect like decompose() does
Particularly valuable when working with:
- Long datasets
- Environmental time series affected by nonlinear changes

STL Decomposition (Loess-based)

stl() uses local regression (loess) to estimate the trend and seasonal components.
s.window = "periodic" specifies that the seasonal component is periodic.
Other options include
- “none” (no seasonal component)
- or a numeric value for the seasonal window size.

plot(decomp)

?stl(co2, s.window = "periodic") |>  
  plot()
#> Help on topic 'plot' was found in the following packages:
#> 
#>   Package               Library
#>   graphics              /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library
#>   base                  /Library/Frameworks/R.framework/Resources/library
#> 
#> 
#> Using the first match ...

Comparing Classical vs STL

Method	Assumes Constant Season?	Robust to Outliers?	Adaptive Smoothing?
decompose	✅ Yes	❌ No	❌ No
stl	✅ or 🔄 (customizable)	✅ Yes	✅ Yes

Recommendation: Use stl() for most real-world environmental time series.

Bringing It All Together

For the CO2 dataset, we can summarize the components of the time series:

Trend: A human fingerprint — atmospheric CO₂ continues to rise year over year
Seasonality: Driven by biospheric rhythms with not multiplicative gains
Remainder: Small, but potentially rich with short-term signals

Understanding these components lets us:

✅ Track long-term progress

✅ Forecast future CO₂

✅ Communicate patterns clearly to policymakers

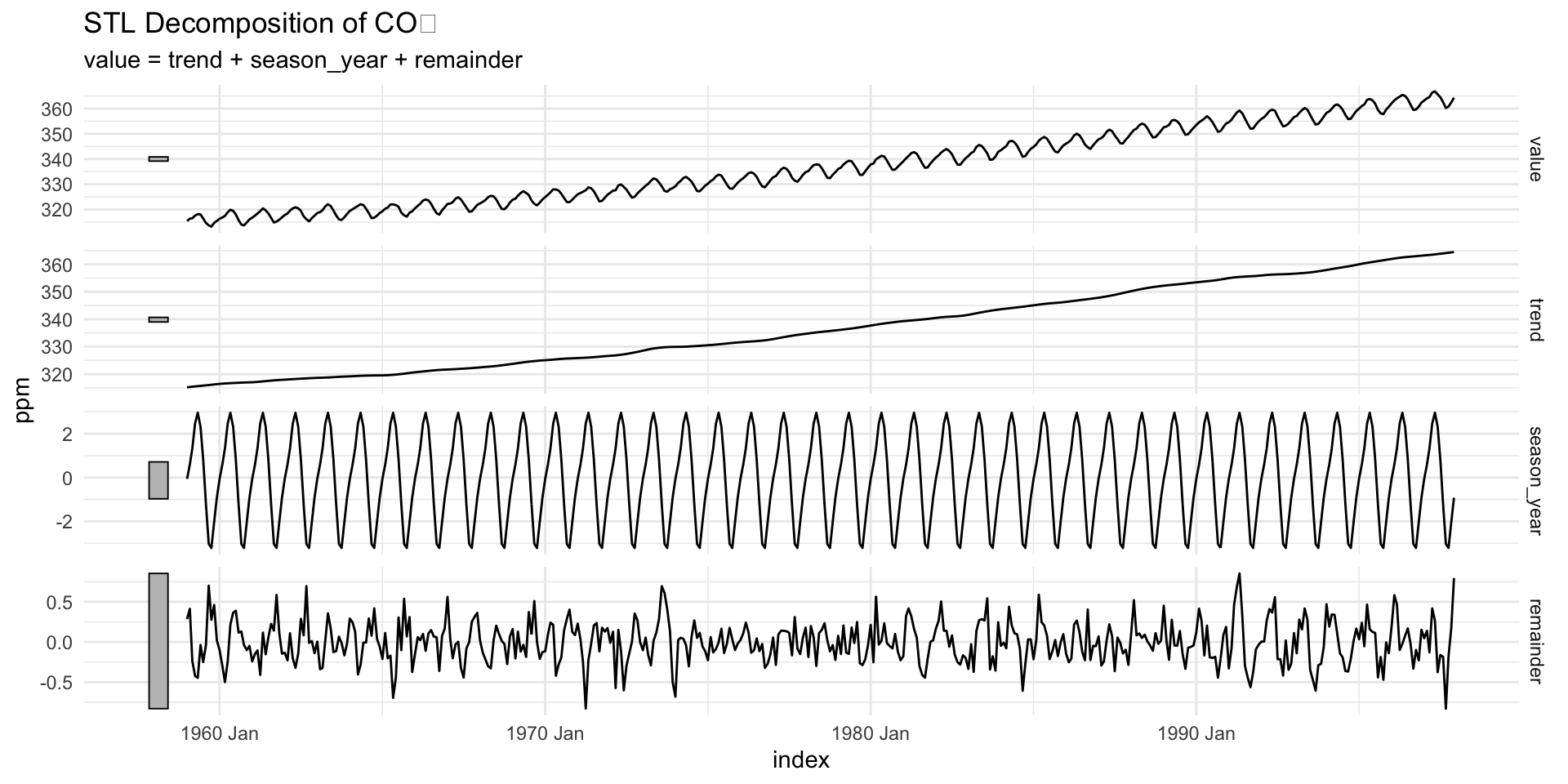
Time Series in the Tidyverse: `tsibble` / `feasts`

tsibble is a tidy data frame for time series data. It extends the tibble class to include time series attributes.
Compatible with dplyr, ggplot2
feasts provides functions for time series analysis and visualization.

co2_tbl <- as_tsibble(co2)
head(co2_tbl)
#> # A tsibble: 6 x 2 [1M]
#>      index value
#>      <mth> <dbl>
#> 1 1959 Jan  315.
#> 2 1959 Feb  316.
#> 3 1959 Mar  316.
#> 4 1959 Apr  318.
#> 5 1959 May  318.
#> 6 1959 Jun  318

Decomposing with `feasts`

`feasts` provides:

a STL() function for seasonal decomposition.
components() extracts the components of the decomposition.
gg_season() and gg_subseries() visualize seasonal patterns.
gg_lag() visualizes autocorrelation and lagged relationships.

co2_decomp <- co2_tbl |>
  model(STL(value ~ season(window = "periodic"))) |>
  components()

glimpse(co2_decomp)
#> Rows: 468
#> Columns: 7
#> Key: .model [1]
#> : value = trend + season_year + remainder
#> $ .model        <chr> "STL(value ~ season(window = \"periodic\"))", "STL(value…
#> $ index         <mth> 1959 Jan, 1959 Feb, 1959 Mar, 1959 Apr, 1959 May, 1959 J…
#> $ value         <dbl> 315.42, 316.31, 316.50, 317.56, 318.13, 318.00, 316.39, …
#> $ trend         <dbl> 315.1954, 315.3023, 315.4093, 315.5147, 315.6201, 315.71…
#> $ season_year   <dbl> -0.06100103, 0.59463870, 1.32899651, 2.46904706, 2.95704…
#> $ remainder     <dbl> 0.28564410, 0.41305456, -0.23825306, -0.42371128, -0.447…
#> $ season_adjust <dbl> 315.4810, 315.7154, 315.1710, 315.0910, 315.1730, 315.68…

Component Access

Autoplot

autoplot(co2_decomp) +
  labs(title = "STL Decomposition of CO₂", y = "ppm") +
  theme_minimal()

Component Access

ggpubr::ggdensity(co2_decomp$remainder, main = "Residual Component")

shapiro.test(co2_decomp$remainder)
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  co2_decomp$remainder
#> W = 0.99485, p-value = 0.1202

Advanced Visualization/Modeling with `feasts`

gg_lag()

A lag plot is a scatterplot of a time series against itself, but with a time shift (or “lag”) applied to one of the series.
It helps us visualize the relationship between current and past values of a time series.

📦 Here’s the simple idea:

You take your CO₂ measurements over time.
Then you make a graph where you plot today’s CO₂ (on the Y-axis)…
…against CO₂ from a few months ago (on the X-axis).
This shows you if the past helps predict the present!

📊 If it makes a curvy shape or a line…

…that means there’s a pattern! Your data remembers what happened before — like a smart friend who learns from their past.
But if the dots look like a big messy spaghetti mess that means the data is random, with no memory of what happened before.

gg_lag()

🧠 Why this is useful:

It helps us see if there are patterns in the data.
It helps us understand how past values affect current values.
It helps us decide if we can use this data to make predictions in the future.

co2_tbl |> 
  gg_lag() +
  labs(title = "Lag Plot of CO₂", x = "Lagged CO₂", y = "Current CO₂") +
  theme_minimal()

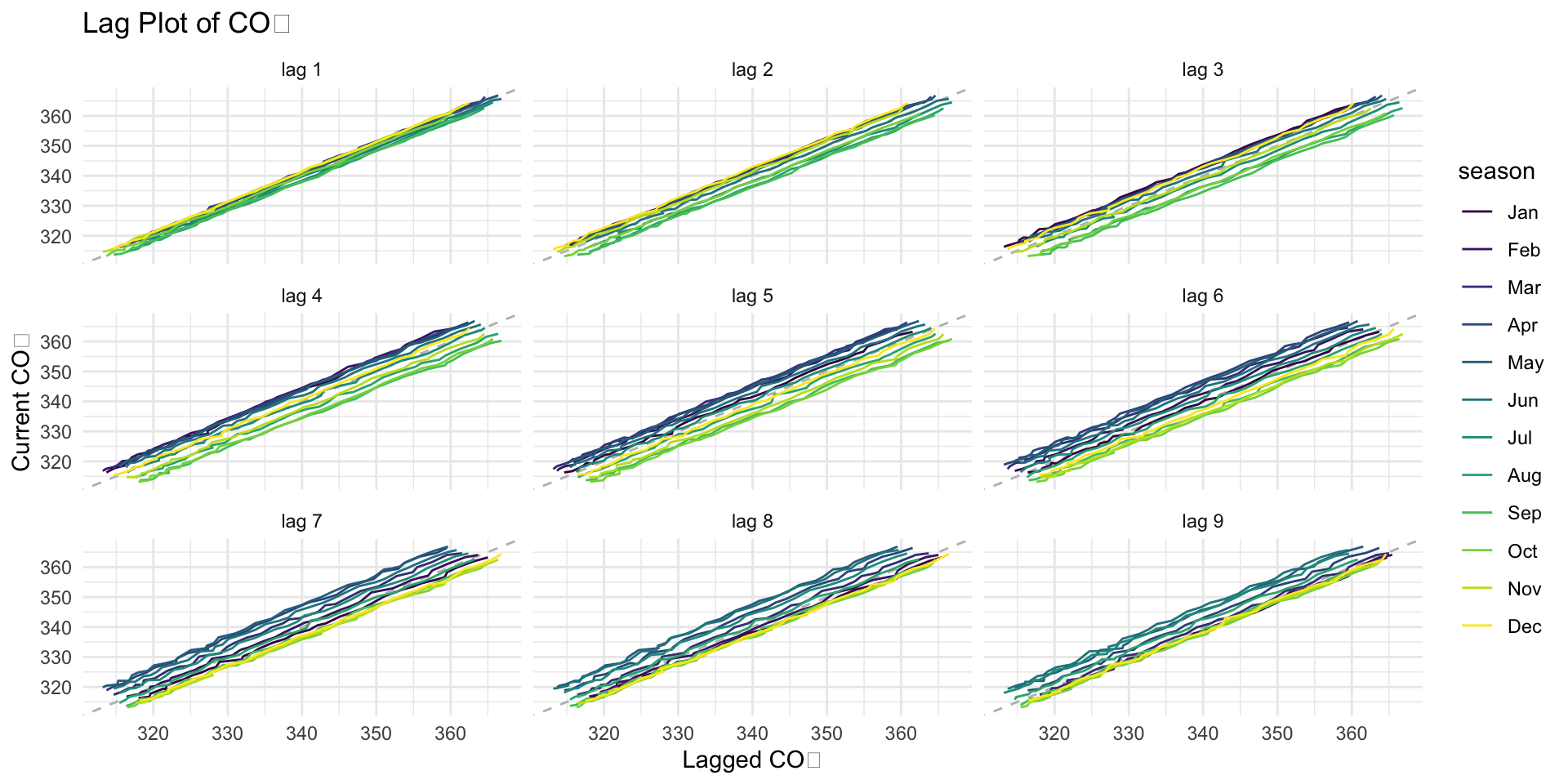
gg_subseries

Imagine the co2 dataset as a big collection of monthly CO₂ data from Mauna Loa. Each month is a group, and each year is a new object
Now, we want to see how each month behaves across the years, so we can spot if January always has higher or lower CO₂ levels, for example.

📊 What this does:

Each month: A different color shows up for each month (like January in blue, February in red, etc.)
Lines: You see the CO₂ values for each month over different years. For example, you might notice that CO₂ levels tend to be higher in the spring and lower in the fall.

🧠 Why this is useful:

We can spot seasonal trends: Does CO₂ rise in the winter? Or fall in the summer?
We can also compare months across the years: Is January more or less CO₂-heavy compared to other months?

gg_subseries()

gg_subseries(co2_tbl) +
  labs(title = "Monthly CO₂ Patterns", y = "CO₂ (ppm)", x = "Year") + 
  theme_minimal()

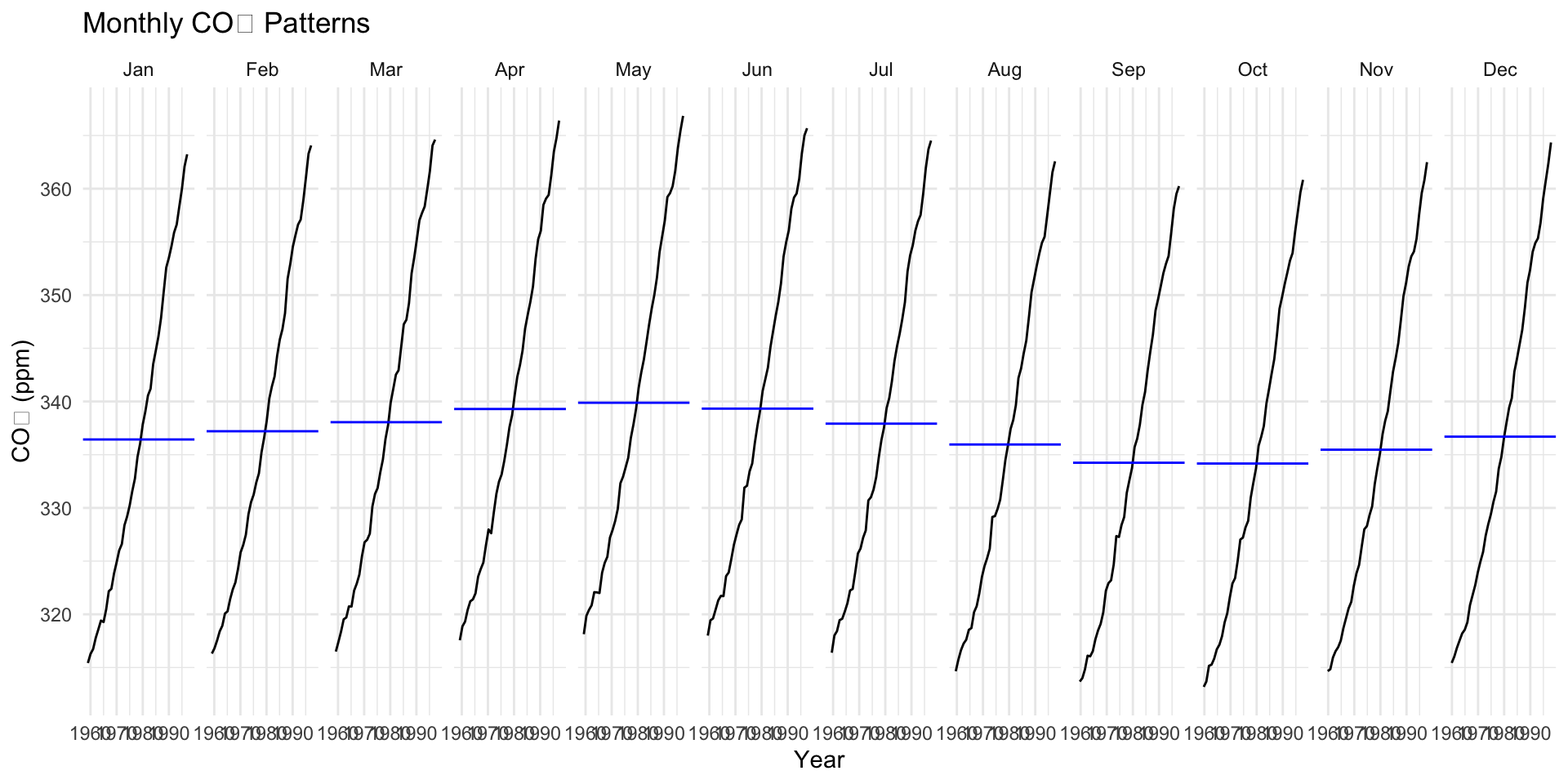
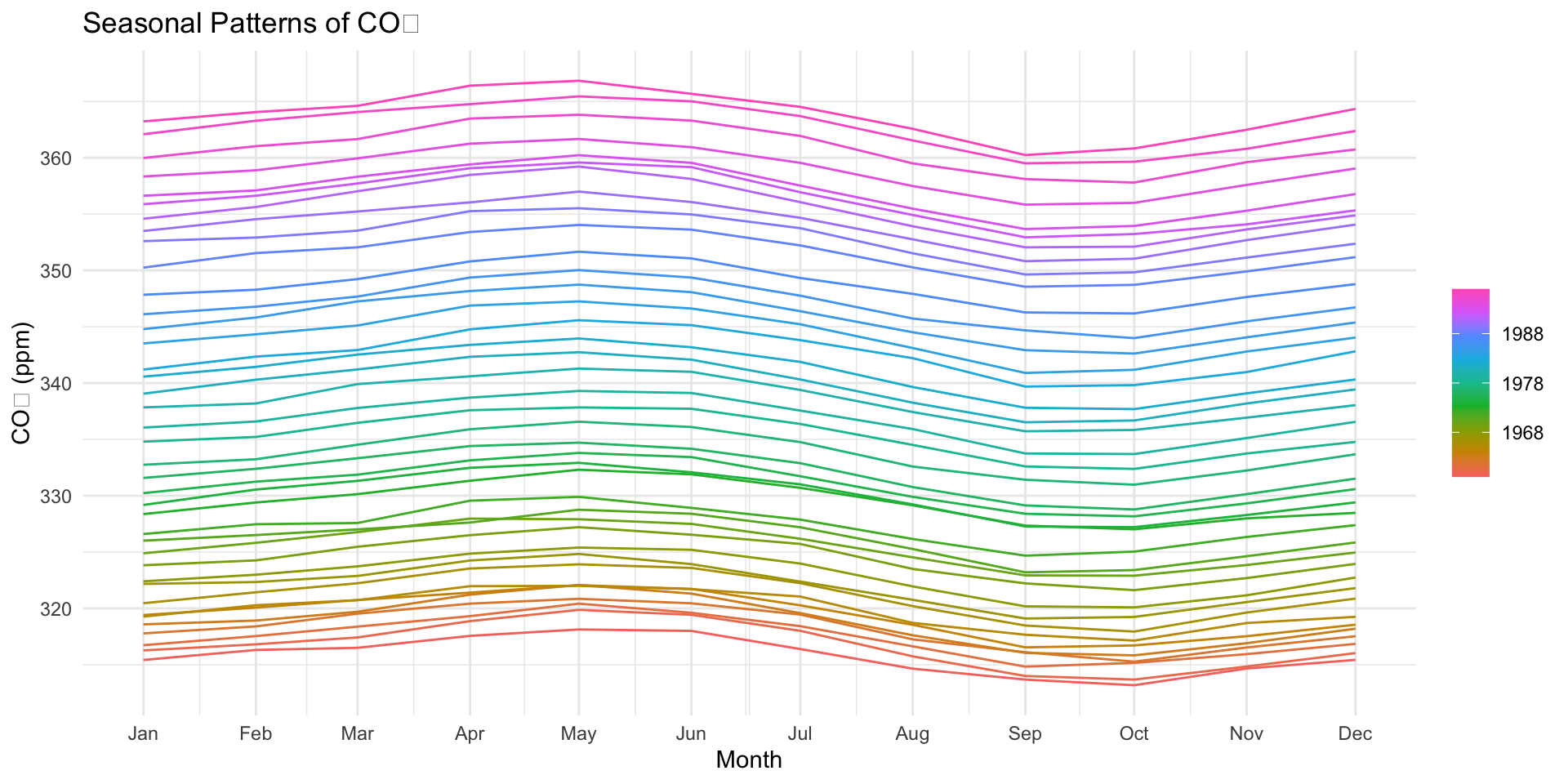
gg_season

Think of gg_season() like a way to look at a yearly picture of CO₂ and see if the Earth follows a seasonal rhythm.
It makes the changes in CO₂ easy to spot when you look at months side-by-side.

📊 What this does:

It shows you how CO₂ changes during each month of the year, but it puts all the years together, so you can see if the same thing happens every year in January, February, and so on.

🧠 Why this is useful:

You’ll see a smooth curve for each month. Each curve shows how CO₂ goes up and down each year in the same pattern.

gg_season

gg_season(co2_tbl) +
  labs(title = "Seasonal Patterns of CO₂", y = "CO₂ (ppm)", x = "Month") +
  theme_minimal()

Bonus: Interactive Plotting

In last weeks demo, we used plotly to generate an interactive plot of the hyperparameter tuning process.
You can use the plotly package to add interactivity to your ggplots directly with ggplotly()!

library(plotly)

co2_plot <- co2_tbl |>
  autoplot() +
  geom_line(color = "steelblue") +
  labs(title = "Interactive CO₂ Time Series", x = "Date", y = "ppm")

Bonus: Interactive Plotting

ggplotly(co2_plot)

Assignment

In this activity, you will download streamflow data from the Cache la Poudre River (USGS site 06752260) and analyze it using a few time series methods.

First, use this code to download the data from the USGS site.

library(dataRetrieval)

# Example: Cache la Poudre River at Mouth (USGS site 06752260)
poudre_flow <- readNWISdv(siteNumber = "06752260",    # Download data from USGS for site 06752260
                          parameterCd = "00060",      # Parameter code 00060 = discharge in cfs)
                          startDate = "2013-01-01",   # Set the start date
                          endDate = "2023-12-31") |>  # Set the end date
  renameNWISColumns() |>                              # Rename columns to standard names (e.g., "Flow", "Date")
  mutate(Date = yearmonth(Date)) |>                   # Convert daily Date values into a year-month format (e.g., "2023 Jan")
  group_by(Date) |>                                   # Group the data by the new monthly Date
  summarise(Flow = mean(Flow))                       # Calculate the average daily flow for each month

Assignment

1. Convert to tsibble

Use as_tsibble() to convert the data.frame into a tsibble object. This will allow you to use the feast functions for time series analysis.

2. Plotting the time series

Use ggplot to plot the time series data. Animate this plot with plotly

3. Subseries

Use gg_subseries to visualize the seasonal patterns in the data. This will help you identify any trends or seasonal cycles in the streamflow data.
Describe what you see in the plot. How are “seasons” defined in this plot? What do you think the “subseries” represent?

4. Decompose

Use the model(STL(...)) pattern to decompose the time series data into its components: trend, seasonality, and residuals. Chose a window that you feel is most appropriate to this data…
Describe what you see in the plot. How do the components change over time? What do you think the trend and seasonal components represent?

Submission

Upload a rendered qmd file to the course website. Make sure to include your code and any plots you created.
This should be an HTML file with self-contained: true.
It should not point to a local host, and must be the physical file.
Make sure to include your code and any plots you created and that the outputs render as you expect.

Lecture 21

Learning Objectives

What is Time Series Data?

Examples:

Why Time Series Matter

Working with Date Objects in R

Base R Date Functions

Date Sequences

Timezones

lubridate Package

lubridate timezones

R Packages for Time Series

When to Use Which Time Series Format?

Key Concepts in Time Series

Introducing the Mauna Loa CO₂ Dataset

Mauna Loa CO₂ Dataset

Initial Plot

Understanding ts Objects

Subsetting and Plotting

Decomposing a Time Series

What is Decomposition?

Additive vs Multiplicative

Example

Why Decompose?

Decompostion in R

Deep Dive: Trend Component

Interpreting the Trend

De-Trending

Deep Dive: Seasonal Component

De-seasonalizing

Deep Dive: Remainder Component

Asssessing Patterns in Error?

Smoothing to Remove Noise

STL Decomposition (Loess-based)

STL Decomposition (Loess-based)

Comparing Classical vs STL

Bringing It All Together

Time Series in the Tidyverse: tsibble / feasts

Decomposing with feasts

feasts provides:

Component Access

Autoplot

Component Access

Advanced Visualization/Modeling with feasts

gg_lag()

gg_lag()

gg_subseries

gg_subseries()

gg_season

gg_season

Bonus: Interactive Plotting

Bonus: Interactive Plotting

Assignment

Assignment

1. Convert to tsibble

2. Plotting the time series

3. Subseries

4. Decompose

Submission

Understanding `ts` Objects

Time Series in the Tidyverse: `tsibble` / `feasts`

Decomposing with `feasts`

`feasts` provides:

Advanced Visualization/Modeling with `feasts`