Lecture 23

Introduction to Simple Features

Spatial Data

(https://mgimond.github.io/Spatial/feature-representation.html)

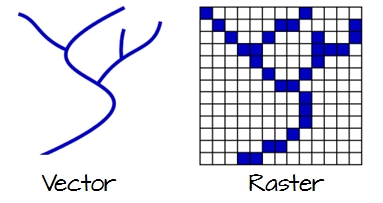
• To work in a GIS environment, real world features (objects or phenomena that can be recorded in 2D or 3D space) need to be reduced to spatial entities.

• These spatial entities can be represented using as a vector data model (this week) or a raster data model (next week).

Vector:

• Vector features can be decomposed into three different geometric primitives:

  1. points
  2. polylines
  3. polygons

• Primitives can be thought of as the “building blocks” for all vector features

• All primitives can be decomposed in to set(s) of numeric X-Y coordinates with a known grid (reference system)

• These reference systems are known as PRØJections, reference systems, etc

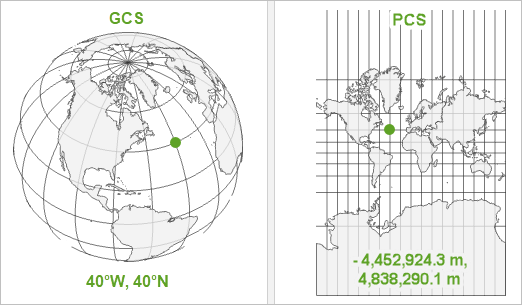
Projections

• Projections can have angular units (lat/lon) - geographic coordinate systems (GCS)

or

• Projections can have distance units (m) - projected coordinate systems (PCS)

Simple Features Model

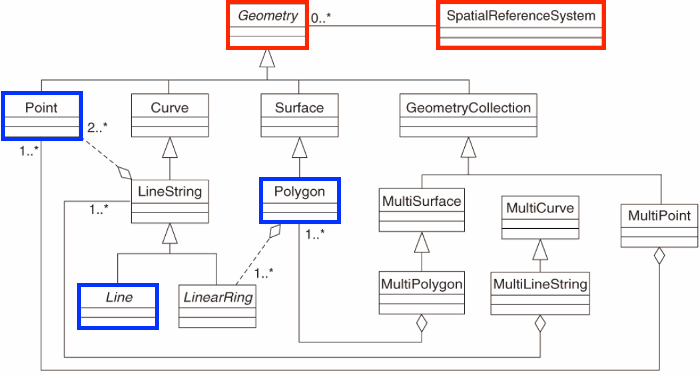
Points

• A point is composed of one coordinate pair in a specific coordinate system.

• Points have no length or area.

ggplot() + 
  geom_point(aes(x = c(1,2,3), y = c(3,1,2))) + 
  labs(x = "X", y = "Y") 

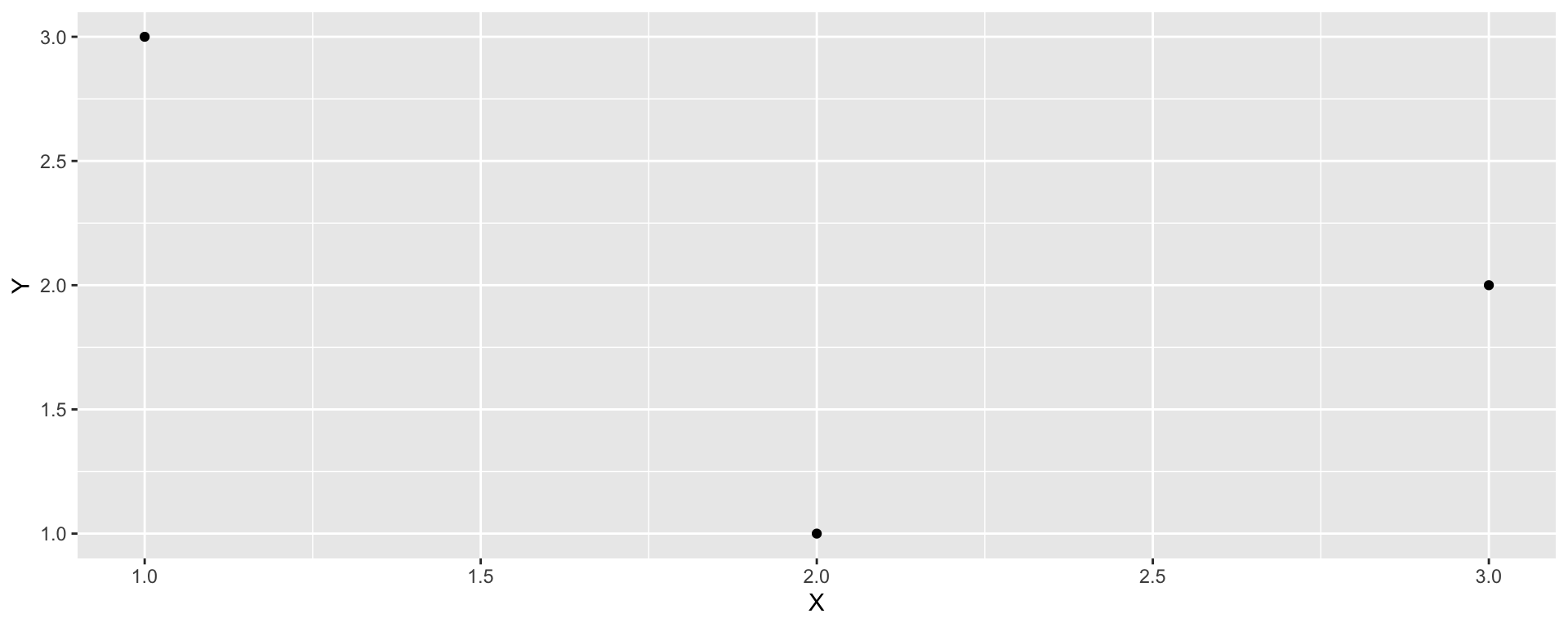
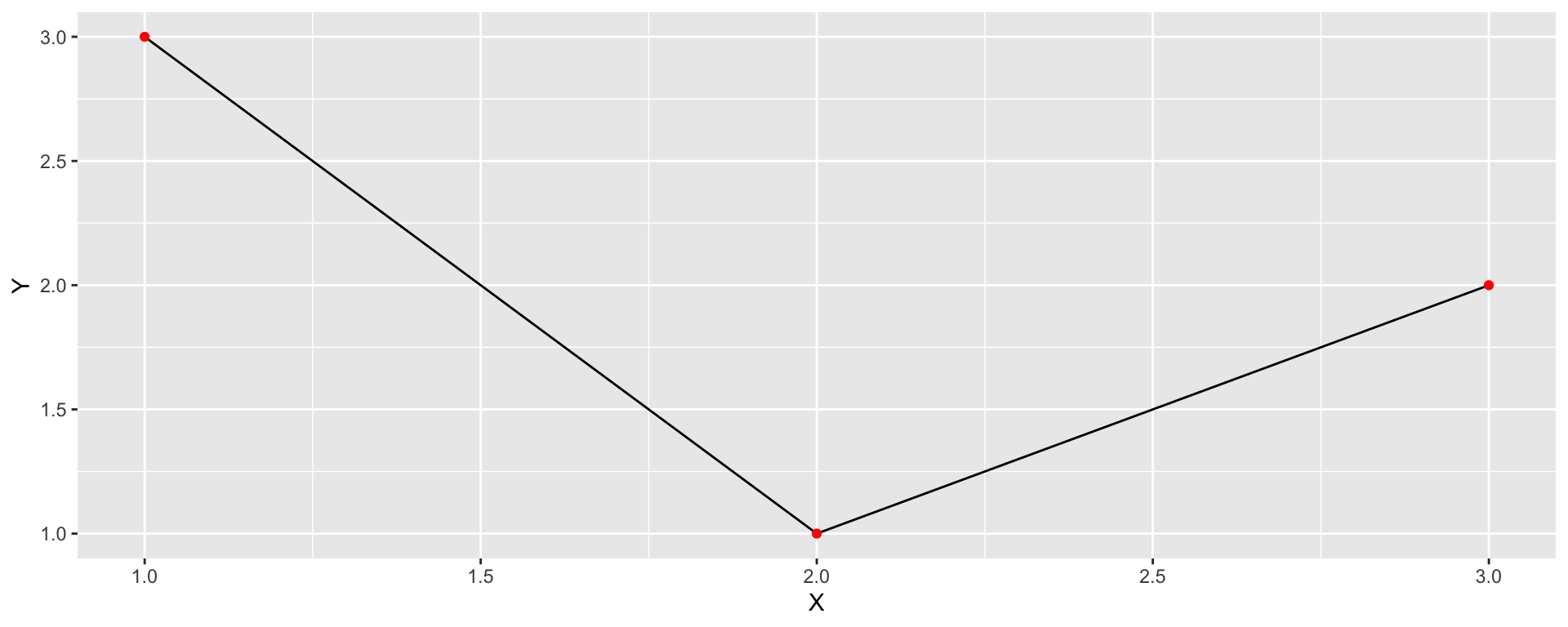
LINESTRING

• A linestring is composed of a ordered sequence of two or more coordinate points

• Points in a line are called vertices and explicitly define the connection between two points.

• A line has length, but no area

ggplot() + 
  geom_line(aes(x = c(1,2,3), y = c(3,1,2))) + 
  geom_point(aes(x = c(1,2,3), y = c(3,1,2)), col = "red") + 
  labs(x = "X", y = "Y") 

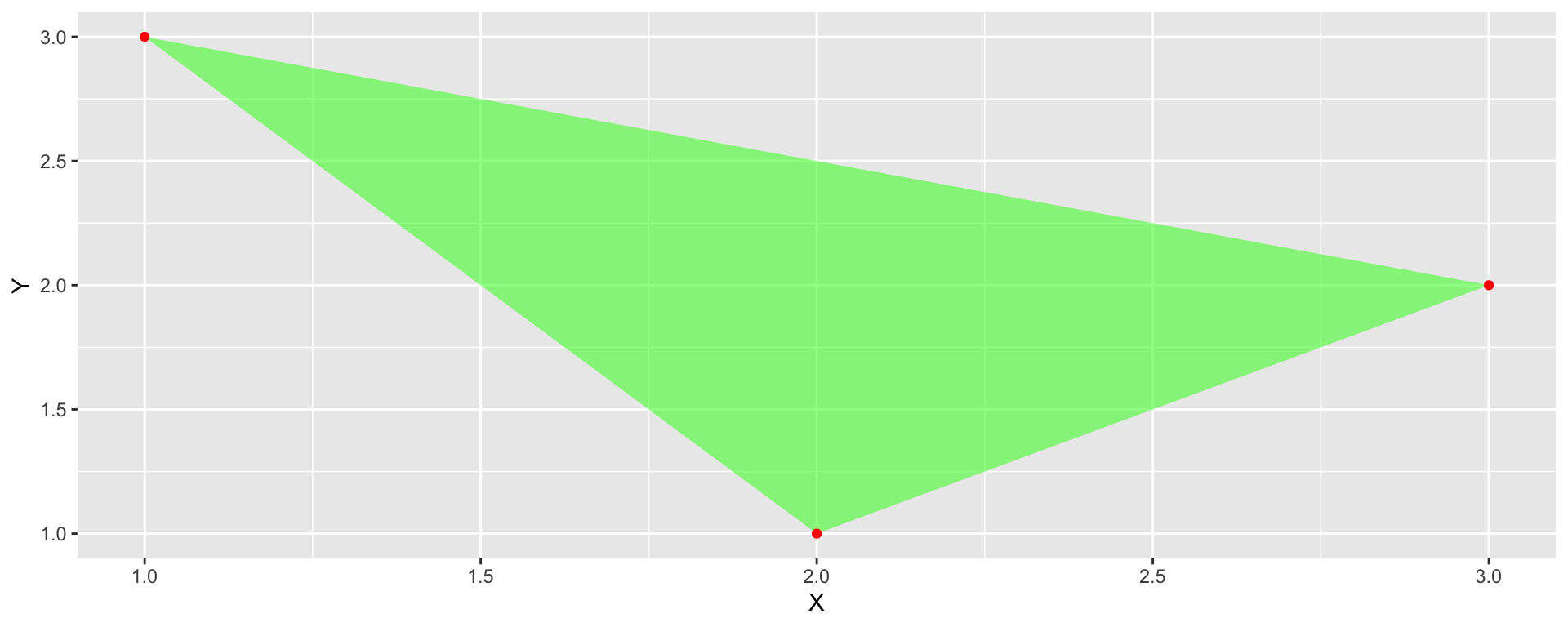
POLYGON

• A polygon is composed of 4 or more points whose starting and ending point are the same.

• Polygons have both length and area.

ggplot() + 
  geom_polygon(aes(x = c(1,2,3,1), y = c(3,1,2,3)), fill = "green", alpha = .5) + 
  geom_point(aes(x = c(1,2,3), y = c(3,1,2)), col = "red") +
  labs(x = "X", y = "Y") 

WKT: Well-Known-Text

Well-known text is a text markup language for representing vector geometry objects.

A binary equivalent, known as well-known binary, is used to transfer and store the same information in a more compact form convenient for computer processing.

#> Simple feature collection with 3 features and 0 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -2032604 ymin: 1468468 xmax: 1833394 ymax: 2178657
#> Projected CRS: NAD83 / Conus Albers
#> # A tibble: 3 × 1
#>             geometry
#>          <POINT [m]>
#> 1  (1833394 2178657)
#> 2 (-2032604 1468468)
#> 3 (684628.5 2122697)

Attribute Tables

• Vector objects can have 0 to many attributes associated with it.

• For example a city (point or polygon) can have a name, population, year founded, etc.

• In R, these attributes are stored in a data.frame, and the geometry is stored as unique field.

#> Simple feature collection with 3 features and 3 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -2032604 ymin: 1468468 xmax: 1833394 ymax: 2178657
#> Projected CRS: NAD83 / Conus Albers
#> # A tibble: 3 × 4
#>   city        state      population           geometry
#>   <chr>       <chr>           <dbl>        <POINT [m]>
#> 1 New York    New York     18832416  (1833394 2178657)
#> 2 Los Angeles California   11885717 (-2032604 1468468)
#> 3 Chicago     Illinois      8489066 (684628.5 2122697)

• In shapefiles, these attributes are stored in a .dbf file, the geometry is stored in a “.shp” file, and they are related through a “.shx” file.

• Typically, these attribute values are what we use to make maps (think GEOG 183 if you’ve taken it!)

The simple feature S3 R object

• Like Date, factor, and POSIXct, a spatial object is an S3 class that extends core primitive types and structures.

nc = st_read(system.file("gpkg/nc.gpkg", package="sf"), quiet = TRUE)
nc[1,]
#> Simple feature collection with 1 feature and 14 fields
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -81.74107 ymin: 36.23436 xmax: -81.23989 ymax: 36.58965
#> Geodetic CRS:  NAD27
#>    AREA PERIMETER CNTY_ CNTY_ID NAME  FIPS FIPSNO CRESS_ID BIR74 SID74 NWBIR74
#> 1 0.114     1.442  1825    1825 Ashe 37009  37009        5  1091     1      10
#>   BIR79 SID79 NWBIR79                           geom
#> 1  1364     0      19 MULTIPOLYGON (((-81.47276 3...
class(nc)
#> [1] "sf"         "data.frame"
typeof(nc)
#> [1] "list"

The simple feature S3 R object

attributes(nc)
#> $names
#>  [1] "AREA"      "PERIMETER" "CNTY_"     "CNTY_ID"   "NAME"      "FIPS"     
#>  [7] "FIPSNO"    "CRESS_ID"  "BIR74"     "SID74"     "NWBIR74"   "BIR79"    
#> [13] "SID79"     "NWBIR79"   "geom"     
#> 
#> $row.names
#>   [1]   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18
#>  [19]  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36
#>  [37]  37  38  39  40  41  42  43  44  45  46  47  48  49  50  51  52  53  54
#>  [55]  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72
#>  [73]  73  74  75  76  77  78  79  80  81  82  83  84  85  86  87  88  89  90
#>  [91]  91  92  93  94  95  96  97  98  99 100
#> 
#> $class
#> [1] "sf"         "data.frame"
#> 
#> $sf_column
#> [1] "geom"
#> 
#> $agr
#>      AREA PERIMETER     CNTY_   CNTY_ID      NAME      FIPS    FIPSNO  CRESS_ID 
#>      <NA>      <NA>      <NA>      <NA>      <NA>      <NA>      <NA>      <NA> 
#>     BIR74     SID74   NWBIR74     BIR79     SID79   NWBIR79 
#>      <NA>      <NA>      <NA>      <NA>      <NA>      <NA> 
#> Levels: constant aggregate identity

Raster

• The raster data model uses an array of cells to represent real-world phenomena and is defined by a resolution (X and Y dimension of the cells), extent and and CRS.

• Raster datasets are commonly used for representing and managing imagery, climate data, elevation models, and other entities.

r = matrix(sample(1:100, 100, replace= TRUE), nrow = 10)
plot(rast(r))

r3D = array(sample(1:100, 200, replace= TRUE), dim = c(10,10,2))
plot(rast(r3D))

Today: Simple features

Simple Features (officially Simple Feature Access) is both an OGC and International Organization for Standardization (ISO) standard that specifies a common storage and access model of (mostly) two-dimensional geometries.

Simple features

Part 1 ISO 19125-1 (SFA-CA for “common architecture”), defines a model for 2D simple features, with linear interpolation between vertices.

The data model defined in SFA-CA is a hierarchy of classes. This part also defines representation using Well-Known Text (and Binary).

Part 2 of the standard, ISO 19125-2 (SFA-SQL), defines an implementation using SQL.

The geometries are also associated with spatial reference systems.

The standard also specifies attributes, methods and assertions with the geometries. - In general, a 2D geometry is simple if it contains no self-intersection. - The specification defines DE-9IM spatial predicates and several spatial operators that can be used to generate new geometries from existing geometries.

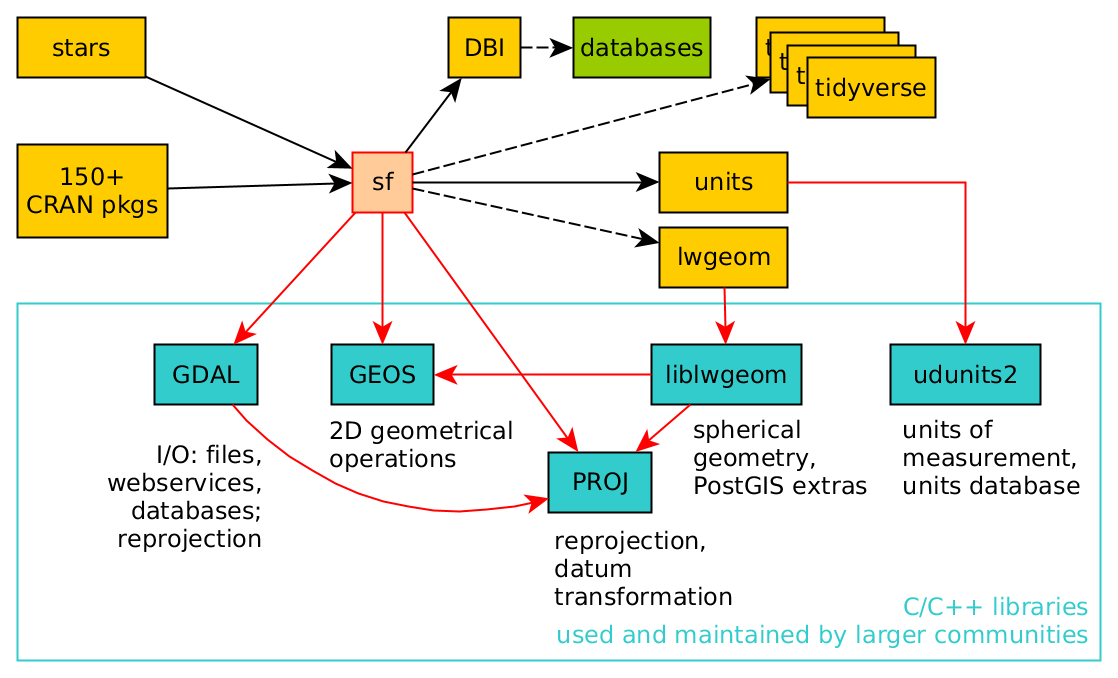
Simple features (sf) package

The sf package implements the Simple Features standard for R

• The sf package contains functions that bind
  • to GDAL for reading and writing data,
  • to GEOS for geometrical operations, and
  • to PRØJ for projection conversions and datum transformations

The source libraries R points to can be checked with:

sf::sf_extSoftVersion()
#>           GEOS           GDAL         proj.4 GDAL_with_GEOS     USE_PROJ_H 
#>       "3.13.0"        "3.8.5"        "9.5.1"         "true"         "true" 
#>           PROJ 
#>        "9.5.1"

Simple features (sf) R package

• represents simple features as records in a data.frame/tibble with a geometry list-column

• represents all 17 simple feature types for all dimensions (XY, XYZ, XYM, XYZM)

• interfaces to GEOS to support geometrical operations including the DE9-IM

• interfaces to GDAL, supporting all driver options

• interfaces to PRØJ for coordinate reference system conversions and transformations

• uses WKB serializations written in C++/Rcpp for fast I/O with GDAL and GEOS

• reads and writes to spatial databases such as PostGIS using DBI

• is extended by lwgeom for further liblwgeom/PostGIS functions, including some spherical geometry functions

Simple features (sf) package

Simple Features

OGC Simple Features

• Simple feature geometries describe the geometries of features.

• The main application of simple feature geometries is to describe 2D geometries as points, lines, or polygons.

• “simple” refers to the fact that line or polygon geometries are represented by set of points connected with straight lines.

• Simple features access is a standard (Herring 2011, Herring (2010), ISO (2004)) for describing simple feature geometries via:

  1. a class hierarchy

  2. a set of operations

  3. binary and text encodings

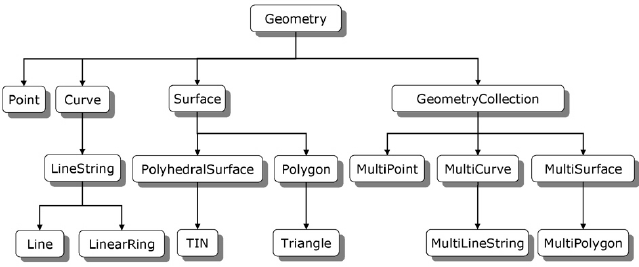
Geometry types

The following 7 simple feature types are the most common, and are the only ones used for GeoJSON:

SINGLE	Description
POINT	zero-dimensional geometry containing a single point
LINESTRING	sequence of points connected by straight, non-self intersecting line pieces; one-dimensional geometry
POLYGON	geometry with a positive area (two-dimensional); sequence of points form a closed, non-self intersecting ring; the first ring denotes the exterior ring, zero or more subsequent rings denote holes in this exterior ring

MULTI (same typed)	Description
MULTIPOINT	set of points; a MULTIPOINT is simple if no two Points in the MULTIPOINT are equal
MULTILINESTRING	set of linestrings
MULTIPOLYGON	set of polygons

Multi-Typed	Description
GEOMETRYCOLLECTION	set of geometries of any type except GEOMETRYCOLLECTION

• The descriptions above were copied from the PostGIS manual.

The remaining geometries 10 are rarer, but increasingly find implementations:

type	description
CIRCULARSTRING	The CIRCULARSTRING is the basic curve type, similar to a LINESTRING in the linear world. A single segment requires three points, the start and end points (first and third) and any other point on the arc. The exception to this is for a closed circle, where the start and end points are the same. In this case the second point MUST be the center of the arc, i.e., the opposite side of the circle. To chain arcs together, the last point of the previous arc becomes the first point of the next arc, just like in LINESTRING. This means that a valid circular string must have an odd number of points greater than 1.
COMPOUNDCURVE	A compound curve is a single, continuous curve that has both curved (circular) segments and linear segments. That means that in addition to having well-formed components, the end point of every component (except the last) must be coincident with the start point of the following component.
CURVEPOLYGON	Example compound curve in a curve polygon: CURVEPOLYGON(COMPOUNDCURVE(CIRCULARSTRING(0 0,2 0, 2 1, 2 3, 4 3),(4 3, 4 5, 1 4, 0 0)), CIRCULARSTRING(1.7 1, 1.4 0.4, 1.6 0.4, 1.6 0.5, 1.7 1) )
MULTICURVE	A MultiCurve is a 1-dimensional GeometryCollection whose elements are Curves, it can include linear strings, circular strings or compound strings.
MULTISURFACE	A MultiSurface is a 2-dimensional GeometryCollection whose elements are Surfaces, all using coordinates from the same coordinate reference system.
CURVE	A Curve is a 1-dimensional geometric object usually stored as a sequence of Points, with the subtype of Curve specifying the form of the interpolation between Points
SURFACE	A Surface is a 2-dimensional geometric object
POLYHEDRALSURFACE	A PolyhedralSurface is a contiguous collection of polygons, which share common boundary segments
TIN	A TIN (triangulated irregular network) is a PolyhedralSurface consisting only of Triangle patches.
TRIANGLE	A Triangle is a polygon with 3 distinct, non-collinear vertices and no interior boundary

Dimensions

All geometries are composed of points

• Points are defined by coordinates in a 2-, 3- or 4-D space.

• In addition to XY coordinates, there are two optional dimensions:

• a Z coordinate, denoting altitude

• an M coordinate (rarely used), denoting some measure

• The M describes a property of the vertex that is independent of the feature.

• It sounds attractive to encode a time as M, however these quickly become invalid once the path self-intersects.

• Both Z and M are found relatively rarely, and software support to do something useful with them is rarer still.

Valid geometries

• Valid geometries obey the following properties:

  • LINESTRINGS shall not self-intersect

  • POLYGON rings shall be closed (last point = first point)

  • POLYGON holes (inner rings) shall be inside their exterior ring

  • POLYGON inner rings shall maximally touch the exterior ring in single points, not over a line

  • POLYGON rings shall not repeat their own path

• If any of the above is not the case, the geometry is not valid.

Empty Geometries

• An important concept in the feature geometry framework is the empty geometry.

• empty geometries serve similar purposes as NA values in vectors (placeholder)

• Empty geometries arise naturally from geometrical operations, for instance:

(e = st_intersection(st_point(c(0,0)), st_point(c(1,1))))
#> GEOMETRYCOLLECTION EMPTY

• It is not entirely clear what the benefit is of having typed empty geometries, but according to the simple feature standard they are type so the sf package abides by that.

• Empty geometries can be detected by:

st_is_empty(e)
#> [1] TRUE

So:

• There are 17 typed geometries supported by the simple feature standard
• All geometries are made up of points
• points can exist in 2,3,4 Dimensional space
• LINESTRING and POLYGON geometries have rules that define validity
• Geometries can be empty (but are still typed)

How simple features are organized in R?

• Simple Features is a standard that is implemented in R (not limited to R)

• So far we have discusses simple features the standard, rather then simple features the implementation

• In R, simple features are implemented using standard data structures (S3 classes, lists, matrix, vector).

• Attributes are stored in data.frames (or tbl_df)

• Feature geometries are stored in a data.frame column.

• Since geometries are not single-valued, they are put in a list-column

• This means each observation (element) is a list itself!

Remember our nested lists?

list(list(c(1:5)))
#> [[1]]
#> [[1]][[1]]
#> [1] 1 2 3 4 5

sfg –> sfc –> sf

sf, sfc, sfg

The three classes are used to represent simple feature objects are:

sf: data.frame with feature attributes and geometries

which contains an:

sfc: the list-column with the geometries for each feature

which is composed of:

sfg: individual simple feature geometries

sf, sfc, sfg

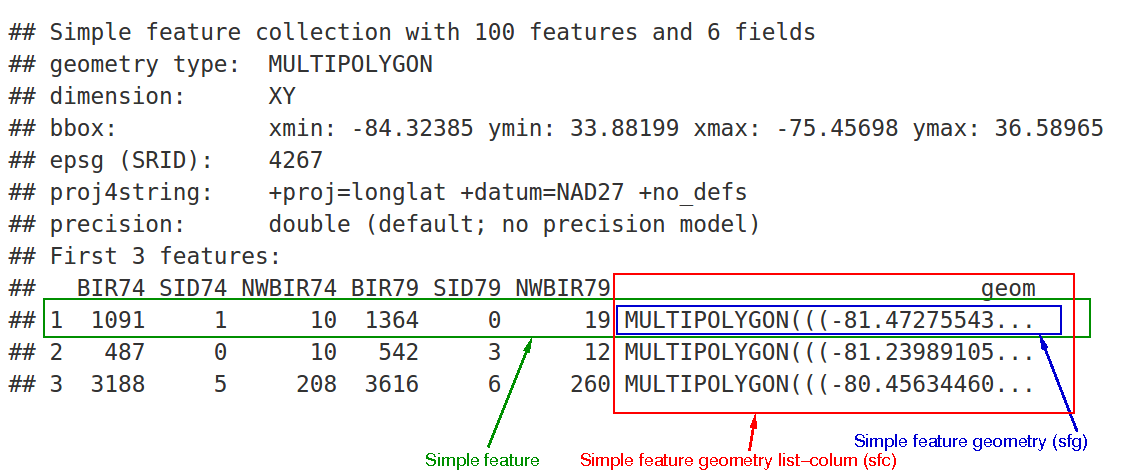
In the output we see:

• in green a simple feature: a single record (row, consisting of attributes and geometry

• in blue a single simple feature geometry (an object of class sfg)

• in red a simple feature list-column (an object of class sfc, which is a column in the data.frame)

• Even though geometries are native R objects, they are printed as well-known text

sfg: simple feature geometry

• Simple feature geometry (sfg) objects carry geometries

• Simple feature geometries are implemented as R native data, using the following rules

  1. a single POINT is a numeric vector

  2. a set of points (e.g. in a LINESTRING or ring of a POLYGON) is a matrix, each row containing a point

  3. any other set is a list

sfc: sets of geometries

• sf provides a dedicated class for handling geometry sets as a list-column called sfc

• We can create such a list column with constructor function st_sfc:

(sfc = st_sfc(st_point(c(0,1)), st_point(c(-3,2))))
#> Geometry set for 2 features 
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -3 ymin: 1 xmax: 0 ymax: 2
#> CRS:           NA
#> POINT (0 1)
#> POINT (-3 2)

The default report from the print method for sfc gives

• the number of features geometries
• the feature geometry type (here: POINT)
• the feature geometry dimension (here: XY)
• the bounding box for the set
• the coordinate reference system for the set (epsg and proj4string)
• the first few geometries, as (abbreviated) WKT

The class of the geometry list-column is a combination of a specific class, and a superclass.

class(sfc)
#> [1] "sfc_POINT" "sfc"

In addition to a class, the sfc object has further attributes (remember S3 class!)

attributes(sfc) |> names()
#> [1] "class"     "precision" "bbox"      "crs"       "n_empty"

which are used to record for the whole set:

• a precision value
• the bounding box enclosing all geometries (for x and y)
• a coordinate reference system
• the number of empty geometries contained in the set

Mixed geometries

Simple feature sets can consist of mixed geometry types:

In this case, the type of the set is GEOMETRY:

(g = st_sfc(st_point(c(0,0)), st_linestring(rbind(c(0,0), c(1,1)))))
#> Geometry set for 2 features 
#> Geometry type: GEOMETRY
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 0 xmax: 1 ymax: 1
#> CRS:           NA
#> POINT (0 0)
#> LINESTRING (0 0, 1 1)

These set can be filtered by using st_is

g |> st_is("LINESTRING")
#> [1] FALSE  TRUE

or, when working with sf objects,

# Note need of %>%
st_sf(g) %>% filter(st_is(., "LINESTRING"))
#> Simple feature collection with 1 feature and 0 fields
#> Geometry type: LINESTRING
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 0 xmax: 1 ymax: 1
#> CRS:           NA
#>                       g
#> 1 LINESTRING (0 0, 1 1)

GEOMETRYCOLLECTION

• Single feature objects can ALSO consist of several geometries types.

• Such cases arise rather naturally when looking for intersections. For instance, the intersection of two LINESTRING geometries may be the combination of a LINESTRING and a POINT.

• Putting this intersection into a single feature needs a GEOMETRYCOLLECTION

#> Geometry set for 1 feature 
#> Geometry type: GEOMETRYCOLLECTION
#> Dimension:     XY
#> Bounding box:  xmin: 1 ymin: -0.5 xmax: 8 ymax: 1.5
#> CRS:           NA
#> GEOMETRYCOLLECTION (POINT (1 0), LINESTRING (4 ...

GEOMETRYCOLLECTION

• In case we end up with GEOMETRYCOLLECTION objects, the next question is often what to do with them. One thing we can do is extract elements from them:

map(j, st_geometry_type) |> unlist()
#> [1] GEOMETRYCOLLECTION
#> 18 Levels: GEOMETRY POINT LINESTRING POLYGON MULTIPOINT ... TRIANGLE

st_collection_extract(j, "POLYGON")
#> Geometry set for 3 features 
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: 5.5 ymin: -0.5 xmax: 8 ymax: 1.5
#> CRS:           NA
#> MULTIPOLYGON (((5.5 0, 7 0, 7 -0.5, 6 -0.5, 5.5...
#> MULTIPOLYGON (((6.6 1, 8 1, 8 1.5, 7 1.5, 6.6 1)))
#> MULTIPOLYGON (((5.5 0, 7 0, 7 -0.5, 6 -0.5, 5.5...

sf: simple feature object

• The sf object is a data.frame with a geometry list-column
• The geometry list-column is of class sfc
• The geometry list-column is the only column that can be of class sfc

co
#> Simple feature collection with 64 features and 4 fields
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS:  WGS 84
#> First 10 features:
#>    geoid       name      aland state_nm                       geometry
#> 1  08001      Adams 3021840487 Colorado MULTIPOLYGON (((-105.0532 3...
#> 2  08003    Alamosa 1871643028 Colorado MULTIPOLYGON (((-105.4855 3...
#> 3  08005   Arapahoe 2066438714 Colorado MULTIPOLYGON (((-103.7065 3...
#> 4  08007  Archuleta 3496712164 Colorado MULTIPOLYGON (((-107.1287 3...
#> 5  08009       Baca 6617400567 Colorado MULTIPOLYGON (((-102.0416 3...
#> 6  08011       Bent 3918255148 Colorado MULTIPOLYGON (((-102.7476 3...
#> 7  08013    Boulder 1881325109 Colorado MULTIPOLYGON (((-105.3978 3...
#> 8  08014 Broomfield   85386685 Colorado MULTIPOLYGON (((-105.1092 3...
#> 9  08015    Chaffee 2624715692 Colorado MULTIPOLYGON (((-105.9698 3...
#> 10 08017   Cheyenne 4605713960 Colorado MULTIPOLYGON (((-103.1729 3...

Conversion between types

We can convert simple feature geometries using the st_cast generic (up to the extent that a conversion is feasible):

methods(st_cast)
#>  [1] st_cast.CIRCULARSTRING*     st_cast.COMPOUNDCURVE*     
#>  [3] st_cast.CURVE*              st_cast.GEOMETRYCOLLECTION*
#>  [5] st_cast.LINESTRING*         st_cast.MULTICURVE*        
#>  [7] st_cast.MULTILINESTRING*    st_cast.MULTIPOINT*        
#>  [9] st_cast.MULTIPOLYGON*       st_cast.MULTISURFACE*      
#> [11] st_cast.POINT*              st_cast.POLYGON*           
#> [13] st_cast.sf*                 st_cast.sfc*               
#> [15] st_cast.sfc_CIRCULARSTRING*
#> see '?methods' for accessing help and source code

Conversion between types

Lets take the Larimer County in our Colorado sf object:

(co1 = AOI::aoi_get(state = "CO", county = "Larimer")$geometry)
#> Geometry set for 1 feature 
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -106.1954 ymin: 40.25778 xmax: -104.9431 ymax: 40.99844
#> Geodetic CRS:  WGS 84
#> MULTIPOLYGON (((-105.6533 40.26046, -105.6094 4...
(co_ls = st_cast(co1, "MULTILINESTRING"))
#> Geometry set for 1 feature 
#> Geometry type: MULTILINESTRING
#> Dimension:     XY
#> Bounding box:  xmin: -106.1954 ymin: 40.25778 xmax: -104.9431 ymax: 40.99844
#> Geodetic CRS:  WGS 84
#> MULTILINESTRING ((-105.6533 40.26046, -105.6094...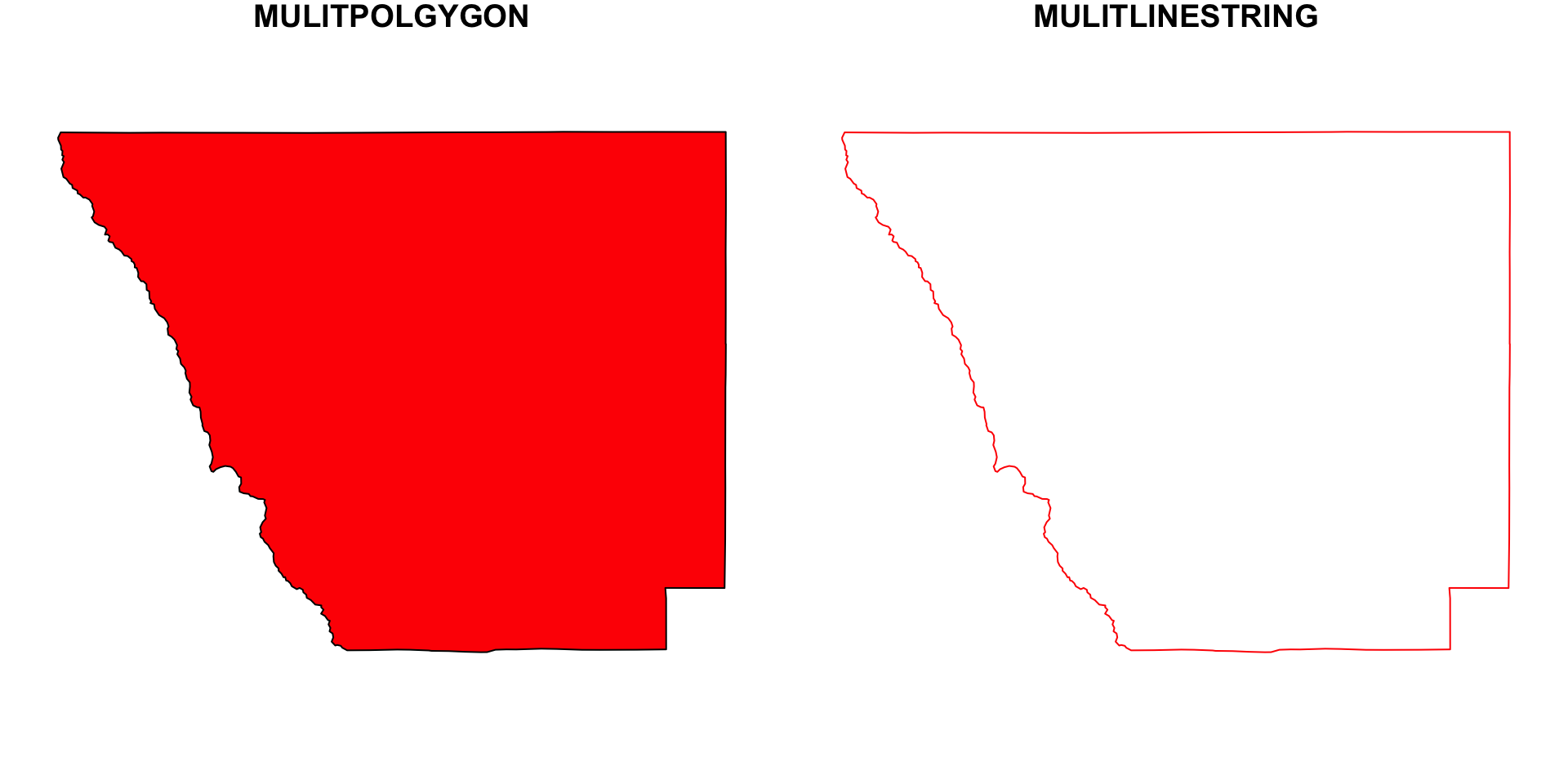

Level of Feature

• The level of the feature is the level of the geometry.

1 LINESTRING (sfg) to 1 POINT (sfg)

rbind(c(0,0), c(1,1), c(1,0), c(0,1)) |>
   st_linestring() |> 
   st_cast("POINT")
#> POINT (0 0)

. . .

1 LINESTRING (sfc) to POINT set (sfc)

rbind(c(0,0), c(1,1), c(1,0), c(0,1)) |>
   st_linestring() |> 
   st_sfc() |> 
   st_cast("POINT")
#> Geometry set for 4 features 
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 0 xmax: 1 ymax: 1
#> CRS:           NA
#> POINT (0 0)
#> POINT (1 1)
#> POINT (1 0)
#> POINT (0 1)

In Reverse …

4 POINTs (sfc) to 4 LINESTRING (sfc)

st_cast(p, "LINESTRING")
#> Geometry set for 4 features 
#> Geometry type: LINESTRING
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 0 xmax: 1 ymax: 1
#> CRS:           NA
#> LINESTRING (0 0)
#> LINESTRING (1 1)
#> LINESTRING (1 0)
#> LINESTRING (0 1)

1 MULTIPOINT POINT (sfc) to 1 LINESTRING (sfc)

st_combine(p) |> 
  st_cast("LINESTRING")
#> Geometry set for 1 feature 
#> Geometry type: LINESTRING
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 0 xmax: 1 ymax: 1
#> CRS:           NA
#> LINESTRING (0 0, 1 1, 1 0, 0 1)

Disolving Geometries Boundaries

Combining geometries preserves their interior boundaries, unioning dissolves the internal boundaries:

(co_geom = co$geometry)
#> Geometry set for 64 features 
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS:  WGS 84
#> First 5 geometries:
#> MULTIPOLYGON (((-105.0532 39.79106, -104.976 39...
#> MULTIPOLYGON (((-105.4855 37.5779, -105.4859 37...
#> MULTIPOLYGON (((-103.7065 39.73989, -103.7239 3...
#> MULTIPOLYGON (((-107.1287 37.42294, -107.2803 3...
#> MULTIPOLYGON (((-102.0416 37.64428, -102.0558 3...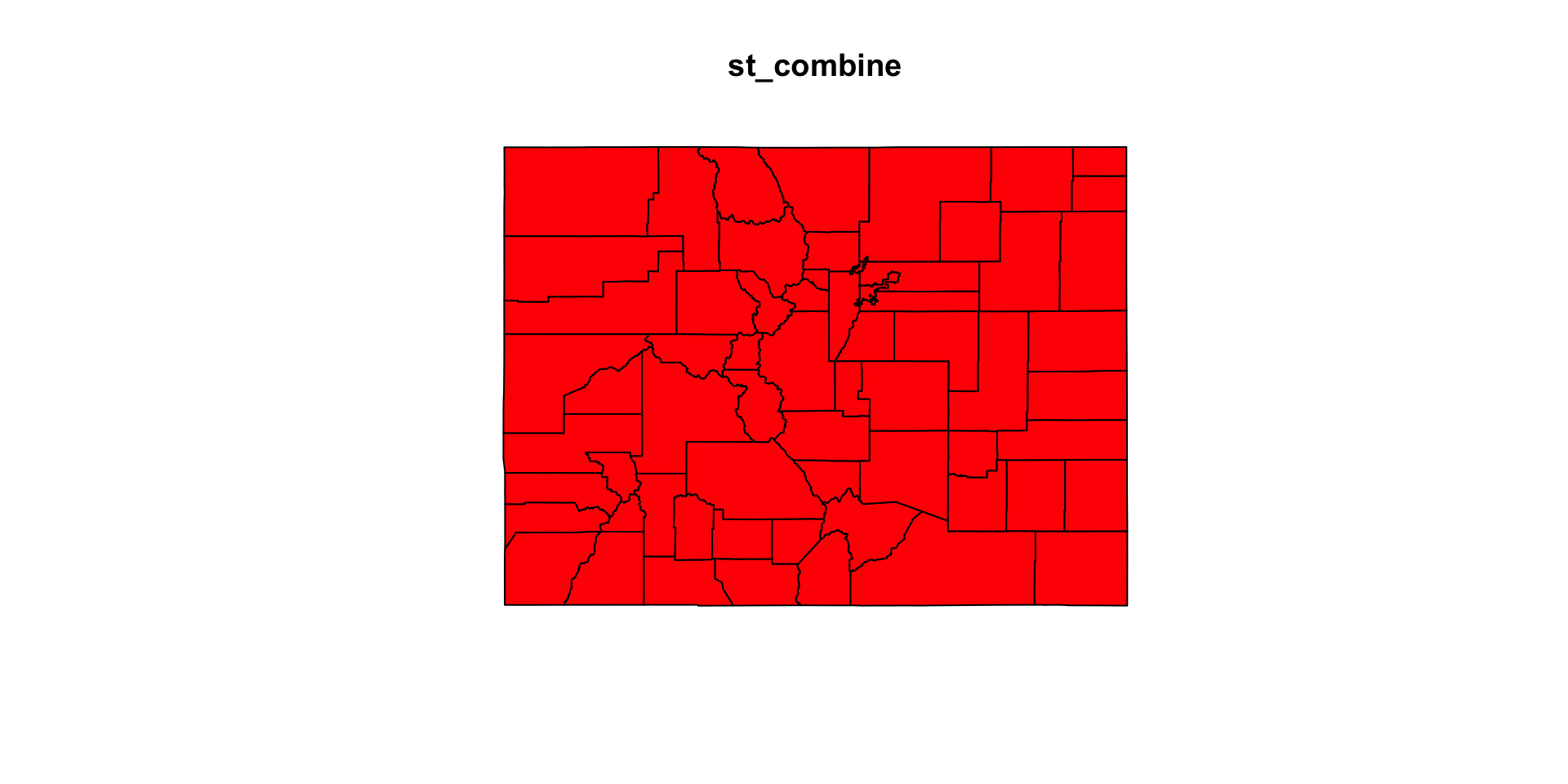

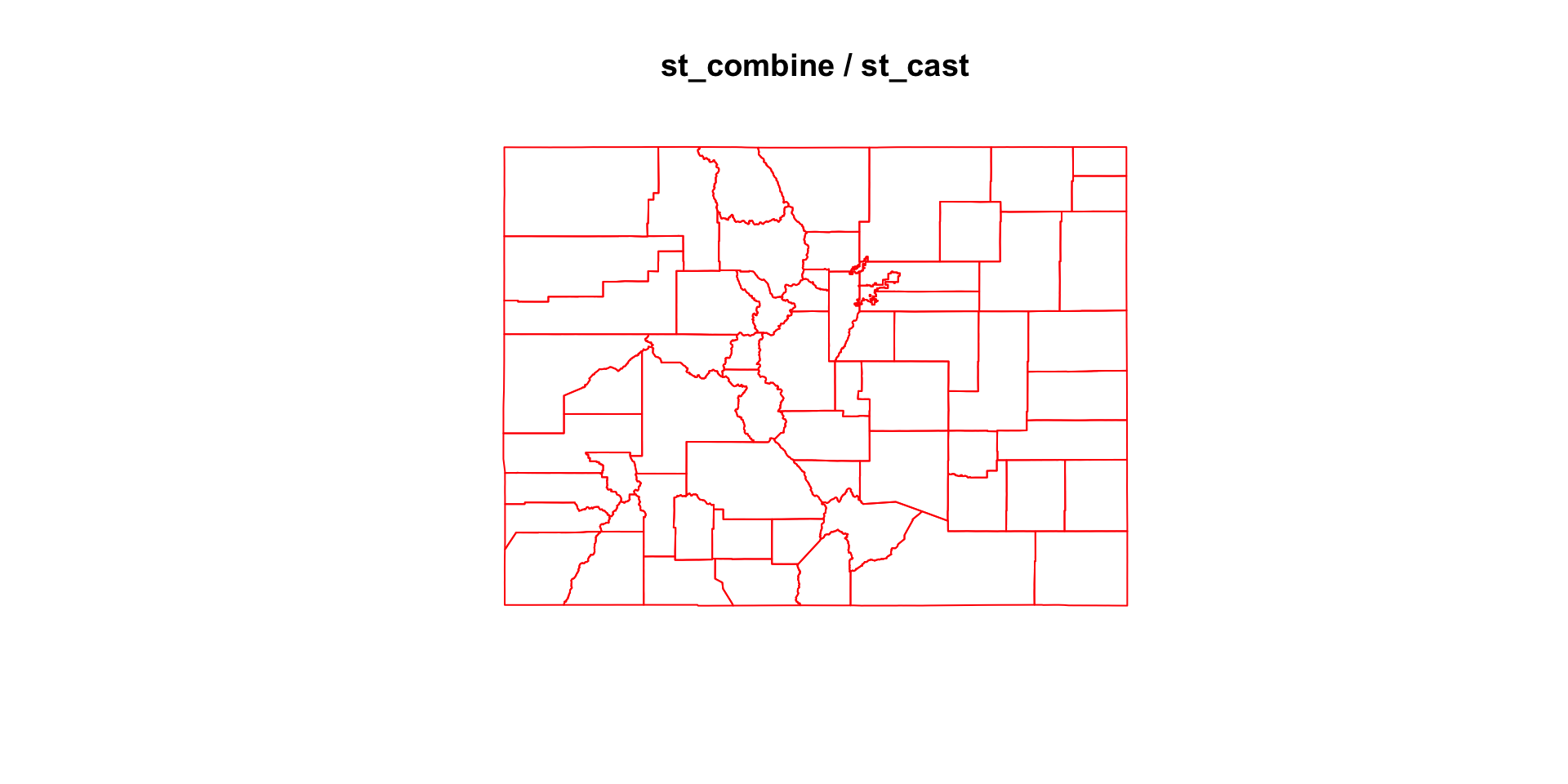
plot(co_geom)

(co_c = st_combine(co_geom))
#> Geometry set for 1 feature 
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS:  WGS 84
#> MULTIPOLYGON (((-105.0532 39.79106, -104.976 39...

(co_u = st_union(co_geom))
#> Geometry set for 1 feature 
#> Geometry type: POLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS:  WGS 84
#> POLYGON ((-105.155 36.99526, -105.1208 36.99543...

(co_c_ml = st_cast(co_c, "MULTILINESTRING"))
#> Geometry set for 1 feature 
#> Geometry type: MULTILINESTRING
#> Dimension:     XY
#> Bounding box:  xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS:  WGS 84
#> MULTILINESTRING ((-105.0532 39.79106, -104.976 ...

(co_u_ml = st_cast(co_u, "MULTILINESTRING"))
#> Geometry set for 1 feature 
#> Geometry type: MULTILINESTRING
#> Dimension:     XY
#> Bounding box:  xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS:  WGS 84
#> MULTILINESTRING ((-105.155 36.99526, -105.1208 ...

The stickness of sfc column

• Geometry columns are “sticky” meaning they persist through data manipulation:

co |> 
  select(name) |> 
  slice(1:2)
#> Simple feature collection with 2 features and 1 field
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -106.0393 ymin: 37.3562 xmax: -103.7057 ymax: 40.00137
#> Geodetic CRS:  WGS 84
#>      name                       geometry
#> 1   Adams MULTIPOLYGON (((-105.0532 3...
#> 2 Alamosa MULTIPOLYGON (((-105.4855 3...

• Dropping the geometry column requires dropping the geometry via sf:

co |> 
  st_drop_geometry() |> #<<
  select(name) |> 
  slice(1:2)
#>      name
#> 1   Adams
#> 2 Alamosa

• Or cohersing the sf object to a data.frame:

co |> 
  as.data.frame() |> #<<
  select(name) |> 
  slice(1:2)
#>      name
#> 1   Adams
#> 2 Alamosa

Spatial Data Science …

Reading and writing (I/O)

As we’ve seen above, reading spatial data from an external file can be done via sf

co <- read_sf("data/co.shp")

Writing takes place in the same fashion, using write_sf:

write_sf(co, "co.shp") # silently overwrites

From Tables (e.g. CSV)

Spatial data can also be created from CSV and other flat files once it is in R:

(cities = read_csv("../labs/data/uscities.csv") |> 
  select(city, state_name, county_name, population, lat, lng) )
#> # A tibble: 31,254 × 6
#>    city         state_name           county_name         population   lat    lng
#>    <chr>        <chr>                <chr>                    <dbl> <dbl>  <dbl>
#>  1 New York     New York             Queens                18832416  40.7  -73.9
#>  2 Los Angeles  California           Los Angeles           11885717  34.1 -118. 
#>  3 Chicago      Illinois             Cook                   8489066  41.8  -87.7
#>  4 Miami        Florida              Miami-Dade             6113982  25.8  -80.2
#>  5 Houston      Texas                Harris                 6046392  29.8  -95.4
#>  6 Dallas       Texas                Dallas                 5843632  32.8  -96.8
#>  7 Philadelphia Pennsylvania         Philadelphia           5696588  40.0  -75.1
#>  8 Atlanta      Georgia              Fulton                 5211164  33.8  -84.4
#>  9 Washington   District of Columbia District of Columb…    5146120  38.9  -77.0
#> 10 Boston       Massachusetts        Suffolk                4355184  42.3  -71.1
#> # ℹ 31,244 more rows

To do this, you must specify the X and the Y coordinate columns as well as a CRS:

• A typical lat/long CRS is EPSG:4326

(cities_sf <- st_as_sf(cities, coords = c("lng", "lat"), crs = 4326))
#> Simple feature collection with 31254 features and 4 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -176.6295 ymin: 17.9559 xmax: 174.111 ymax: 71.2727
#> Geodetic CRS:  WGS 84
#> # A tibble: 31,254 × 5
#>    city         state_name      county_name population            geometry
#>  * <chr>        <chr>           <chr>            <dbl>         <POINT [°]>
#>  1 New York     New York        Queens        18832416  (-73.9249 40.6943)
#>  2 Los Angeles  California      Los Angeles   11885717 (-118.4068 34.1141)
#>  3 Chicago      Illinois        Cook           8489066  (-87.6866 41.8375)
#>  4 Miami        Florida         Miami-Dade     6113982   (-80.2101 25.784)
#>  5 Houston      Texas           Harris         6046392   (-95.3885 29.786)
#>  6 Dallas       Texas           Dallas         5843632  (-96.7667 32.7935)
#>  7 Philadelphia Pennsylvania    Philadelph…    5696588  (-75.1339 40.0077)
#>  8 Atlanta      Georgia         Fulton         5211164   (-84.422 33.7628)
#>  9 Washington   District of Co… District o…    5146120  (-77.0163 38.9047)
#> 10 Boston       Massachusetts   Suffolk        4355184  (-71.0852 42.3188)
#> # ℹ 31,244 more rows

Data Manipulation

• Since sf objects are data.frames, our dplyr verbs work!

• Lets find the most populous city in each Colorado county…

sf and dplyr

cities_sf

#> Simple feature collection with 31254 features and 4 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -176.6295 ymin: 17.9559 xmax: 174.111 ymax: 71.2727
#> Geodetic CRS:  WGS 84
#> # A tibble: 31,254 × 5
#>    city         state_name      county_name population            geometry
#>  * <chr>        <chr>           <chr>            <dbl>         <POINT [°]>
#>  1 New York     New York        Queens        18832416  (-73.9249 40.6943)
#>  2 Los Angeles  California      Los Angeles   11885717 (-118.4068 34.1141)
#>  3 Chicago      Illinois        Cook           8489066  (-87.6866 41.8375)
#>  4 Miami        Florida         Miami-Dade     6113982   (-80.2101 25.784)
#>  5 Houston      Texas           Harris         6046392   (-95.3885 29.786)
#>  6 Dallas       Texas           Dallas         5843632  (-96.7667 32.7935)
#>  7 Philadelphia Pennsylvania    Philadelph…    5696588  (-75.1339 40.0077)
#>  8 Atlanta      Georgia         Fulton         5211164   (-84.422 33.7628)
#>  9 Washington   District of Co… District o…    5146120  (-77.0163 38.9047)
#> 10 Boston       Massachusetts   Suffolk        4355184  (-71.0852 42.3188)
#> # ℹ 31,244 more rows

sf and dplyr

cities_sf |>
  filter(state_name == "Colorado")

#> Simple feature collection with 477 features and 4 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -109.0066 ymin: 37.0155 xmax: -102.0804 ymax: 40.9849
#> Geodetic CRS:  WGS 84
#> # A tibble: 477 × 5
#>    city             state_name county_name population            geometry
#>  * <chr>            <chr>      <chr>            <dbl>         <POINT [°]>
#>  1 Denver           Colorado   Denver         2691349  (-104.8758 39.762)
#>  2 Colorado Springs Colorado   El Paso         638421 (-104.7605 38.8674)
#>  3 Aurora           Colorado   Arapahoe        390201 (-104.7237 39.7083)
#>  4 Fort Collins     Colorado   Larimer         339256 (-105.0656 40.5477)
#>  5 Lakewood         Colorado   Jefferson       156309 (-105.1172 39.6977)
#>  6 Greeley          Colorado   Weld            143554 (-104.7706 40.4152)
#>  7 Thornton         Colorado   Adams           142878 (-104.9438 39.9197)
#>  8 Grand Junction   Colorado   Mesa            141008 (-108.5673 39.0877)
#>  9 Arvada           Colorado   Jefferson       122835   (-105.151 39.832)
#> 10 Boulder          Colorado   Boulder         120121 (-105.2524 40.0248)
#> # ℹ 467 more rows

sf and dplyr

cities_sf |>
  filter(state_name == "Colorado") |>
  group_by(county_name)

#> Simple feature collection with 477 features and 4 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -109.0066 ymin: 37.0155 xmax: -102.0804 ymax: 40.9849
#> Geodetic CRS:  WGS 84
#> # A tibble: 477 × 5
#> # Groups:   county_name [64]
#>    city             state_name county_name population            geometry
#>    <chr>            <chr>      <chr>            <dbl>         <POINT [°]>
#>  1 Denver           Colorado   Denver         2691349  (-104.8758 39.762)
#>  2 Colorado Springs Colorado   El Paso         638421 (-104.7605 38.8674)
#>  3 Aurora           Colorado   Arapahoe        390201 (-104.7237 39.7083)
#>  4 Fort Collins     Colorado   Larimer         339256 (-105.0656 40.5477)
#>  5 Lakewood         Colorado   Jefferson       156309 (-105.1172 39.6977)
#>  6 Greeley          Colorado   Weld            143554 (-104.7706 40.4152)
#>  7 Thornton         Colorado   Adams           142878 (-104.9438 39.9197)
#>  8 Grand Junction   Colorado   Mesa            141008 (-108.5673 39.0877)
#>  9 Arvada           Colorado   Jefferson       122835   (-105.151 39.832)
#> 10 Boulder          Colorado   Boulder         120121 (-105.2524 40.0248)
#> # ℹ 467 more rows

sf and dplyr

cities_sf |>
  filter(state_name == "Colorado") |>
  group_by(county_name) |>
  slice_max(population, n = 1)

#> Simple feature collection with 64 features and 4 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -108.9071 ymin: 37.1751 xmax: -102.2627 ymax: 40.9849
#> Geodetic CRS:  WGS 84
#> # A tibble: 64 × 5
#> # Groups:   county_name [64]
#>    city           state_name county_name population            geometry
#>    <chr>          <chr>      <chr>            <dbl>         <POINT [°]>
#>  1 Thornton       Colorado   Adams           142878 (-104.9438 39.9197)
#>  2 Alamosa        Colorado   Alamosa           9847  (-105.877 37.4752)
#>  3 Aurora         Colorado   Arapahoe        390201 (-104.7237 39.7083)
#>  4 Pagosa Springs Colorado   Archuleta         1718 (-107.0307 37.2675)
#>  5 Springfield    Colorado   Baca              1482  (-102.6189 37.405)
#>  6 Las Animas     Colorado   Bent              2480 (-103.2236 38.0695)
#>  7 Boulder        Colorado   Boulder         120121 (-105.2524 40.0248)
#>  8 Broomfield     Colorado   Broomfield       75110 (-105.0526 39.9542)
#>  9 Salida         Colorado   Chaffee           5786 (-105.9979 38.5298)
#> 10 Cheyenne Wells Colorado   Cheyenne           949 (-102.3521 38.8192)
#> # ℹ 54 more rows

sf and dplyr

cities_sf |>
  filter(state_name == "Colorado") |>
  group_by(county_name) |>
  slice_max(population, n = 1) ->
  co_cities

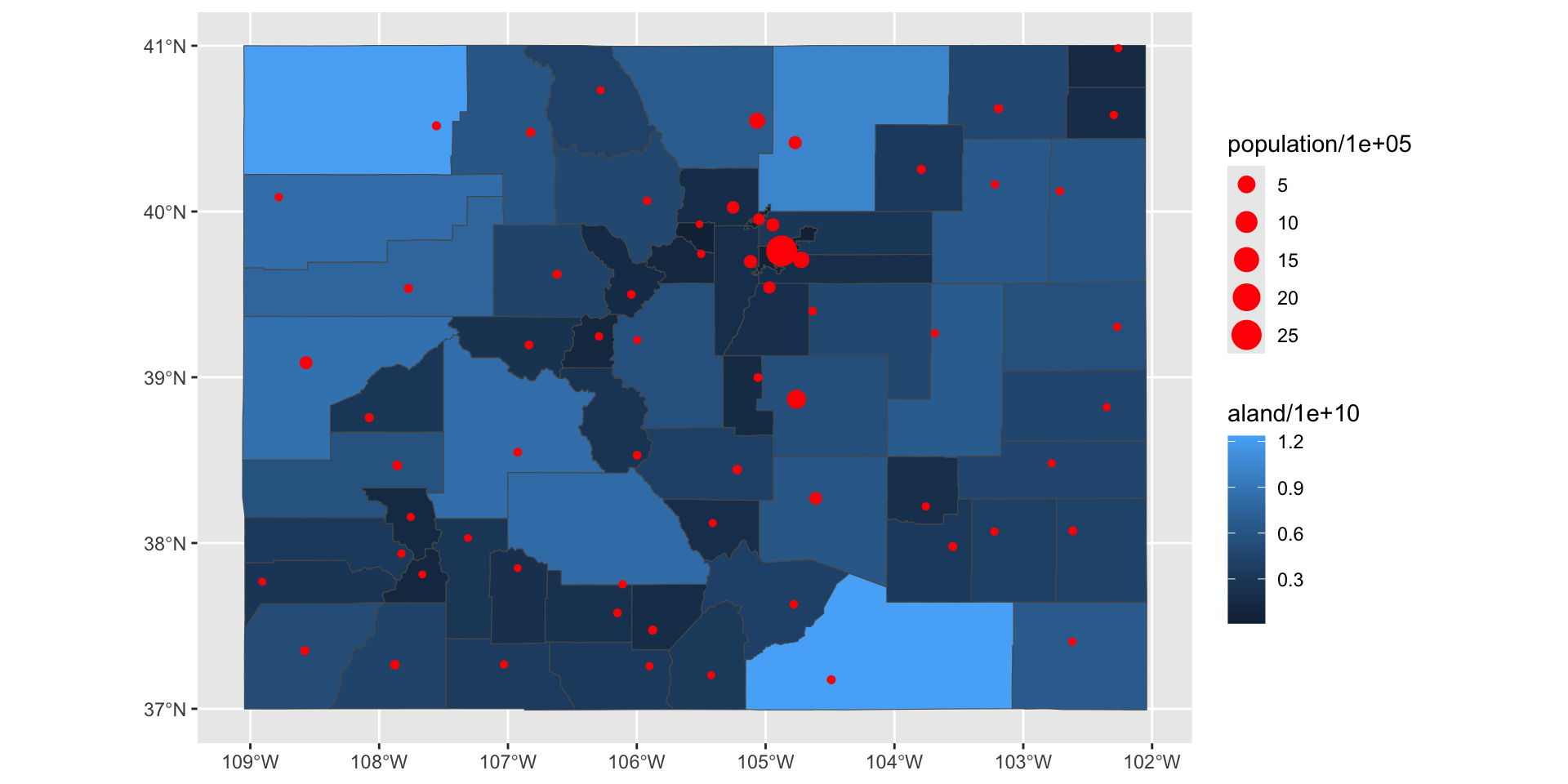
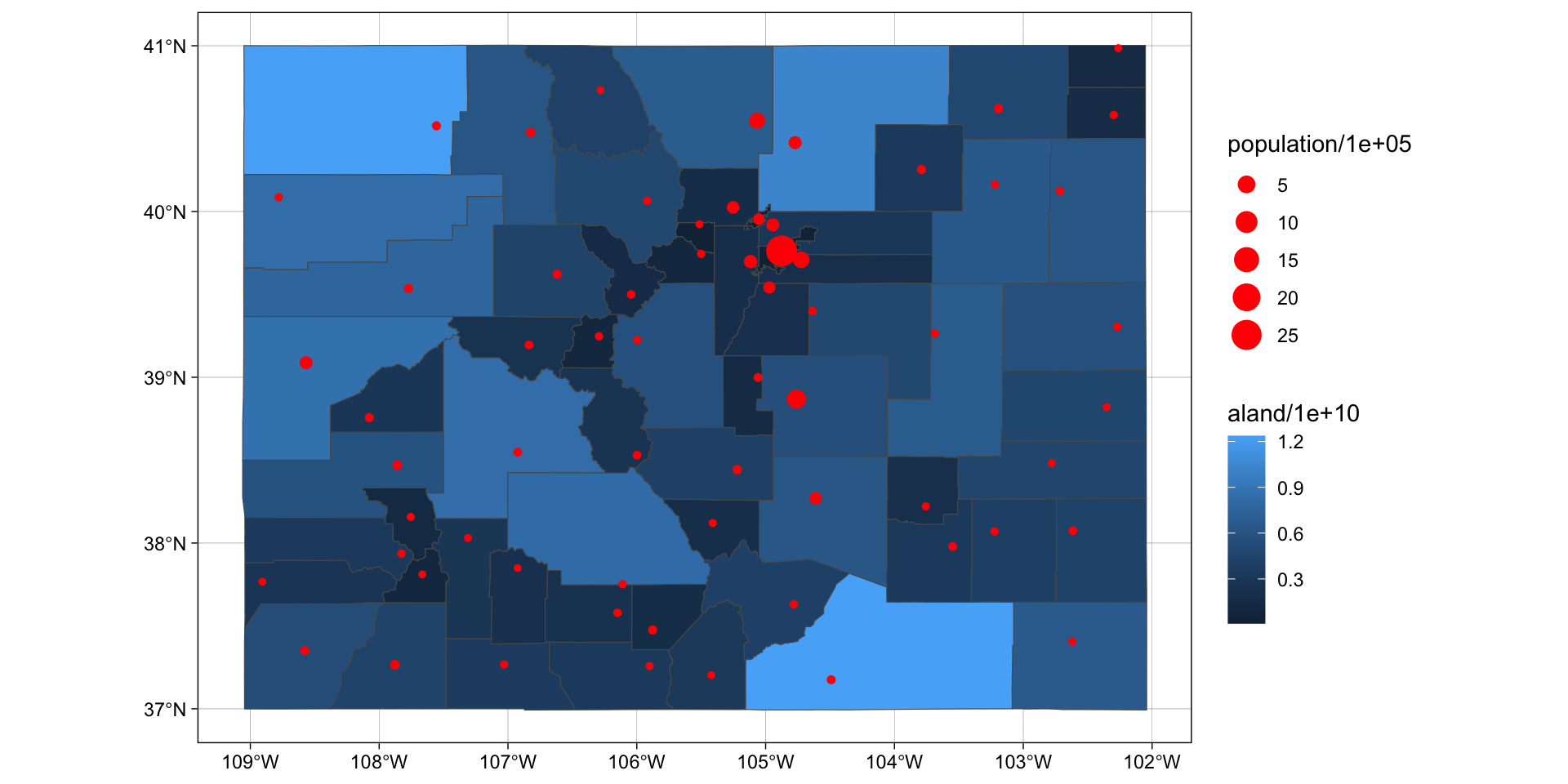
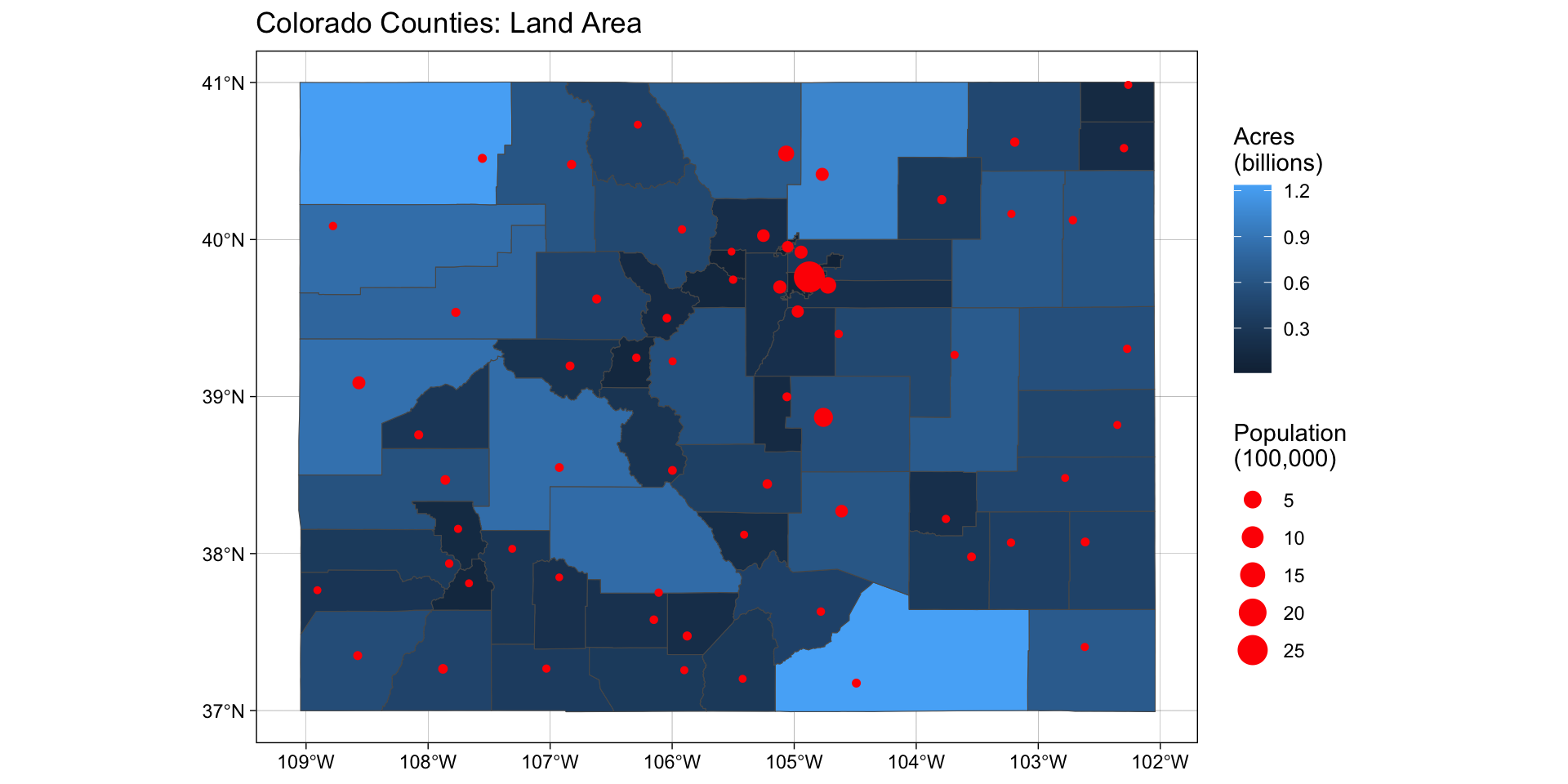
Plotting

• We’ve already seen that ggplot() is a powerful visualization tool:

  1. canvas
  2. layers (geoms)
  3. labels
  4. facets
  5. themes

• spatial work in R is becoming so common that ggplot() comes with a sf geom (geom_sf)

sf an ggplot

ggplot()

sf an ggplot

ggplot() +
  geom_sf(data = co, aes(fill = aland/1e10))

sf an ggplot

ggplot() +
  geom_sf(data = co, aes(fill = aland/1e10)) +
  geom_sf(data = co_cities, aes(size = population/1e5), col = "red")

sf an ggplot

ggplot() +
  geom_sf(data = co, aes(fill = aland/1e10)) +
  geom_sf(data = co_cities, aes(size = population/1e5), col = "red") +
  theme_linedraw()

sf an ggplot

ggplot() +
  geom_sf(data = co, aes(fill = aland/1e10)) +
  geom_sf(data = co_cities, aes(size = population/1e5), col = "red") +
  theme_linedraw() +
  labs(title = "Colorado Counties: Land Area",
       size = "Population \n(100,000)",
       fill = "Acres \n(billions)")

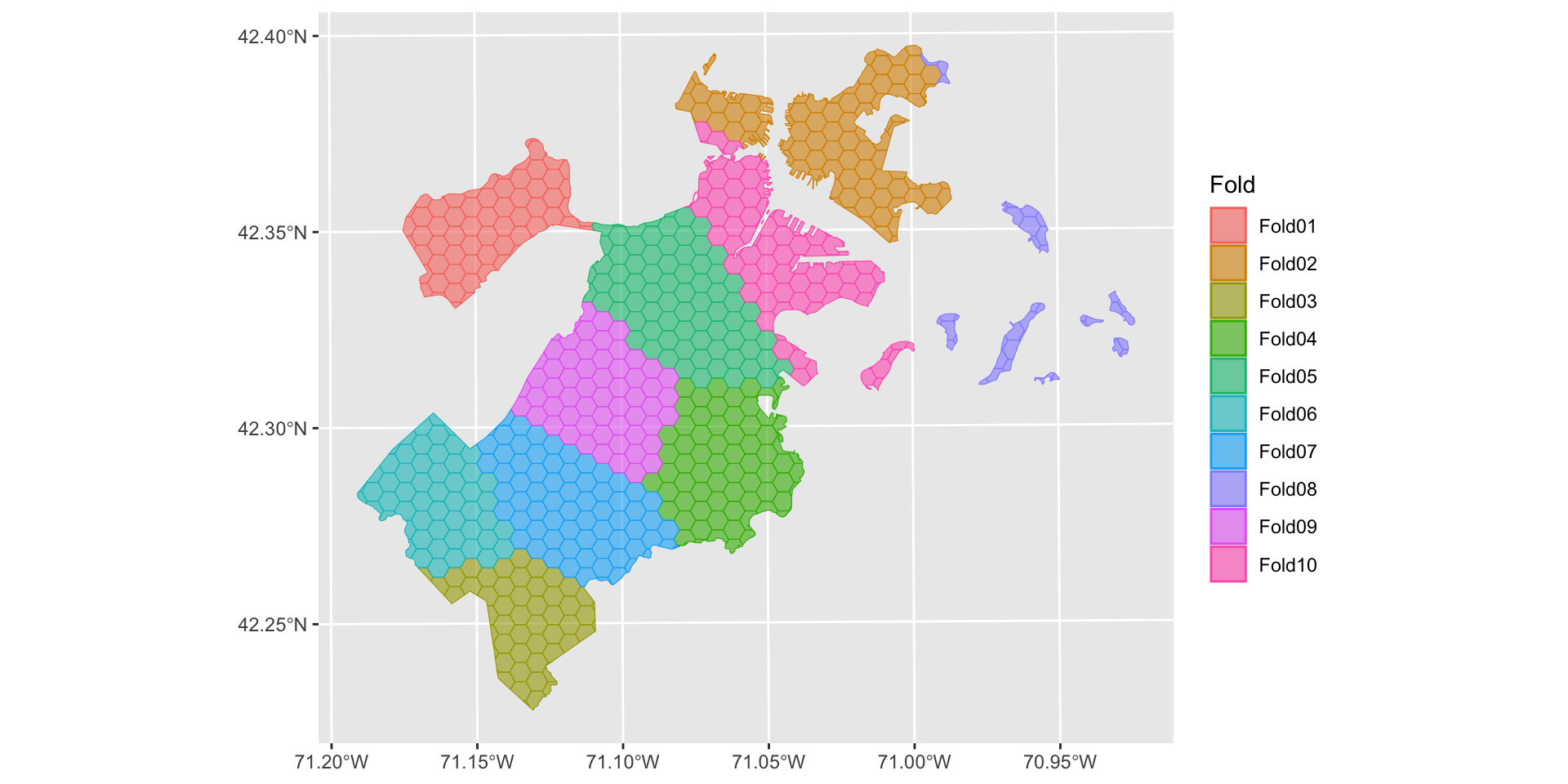
Spatial Sampling

• Spatial sampling is a common task in spatial data science.

Like rsample, spatialsample provides building blocks for creating and analyzing resamples of a spatial data set but does not include code for modeling or computing statistics.

library(spatialsample)

ggplot(boston_canopy) + 
  geom_sf() + 
  theme_linedraw() + 
  labs(title = "Boston Canopy Cover")

set.seed(1234)
folds <- spatial_clustering_cv(boston_canopy, v = 10)

autoplot(folds)

Assignment

For today’s assignment, lets ensure we have our spatial data environment set up:

• To do this install: sf (vector), terra (raster), mapview (interactive mapping) from CRAN (install.packages())

• Then, install the AOI package from GitHub: remotes::install_github("mikejohnson51/AOI")

Assignment

• To ensure you have everything set up correctly, run the following code:

sf::sf_extSoftVersion()
#>           GEOS           GDAL         proj.4 GDAL_with_GEOS     USE_PROJ_H 
#>       "3.13.0"        "3.8.5"        "9.5.1"         "true"         "true" 
#>           PROJ 
#>        "9.5.1"

terra::gdal()
#> [1] "3.8.5"

• And report the values to the Canvas dropbox.

• Additionally, take some time to research GDAL, GEOS, and PROJ. Submit a sentence or two describing each and their role in spatial infrastructure and the value of having direct access to CLI interfaces in a functional langaugelanguage like R …