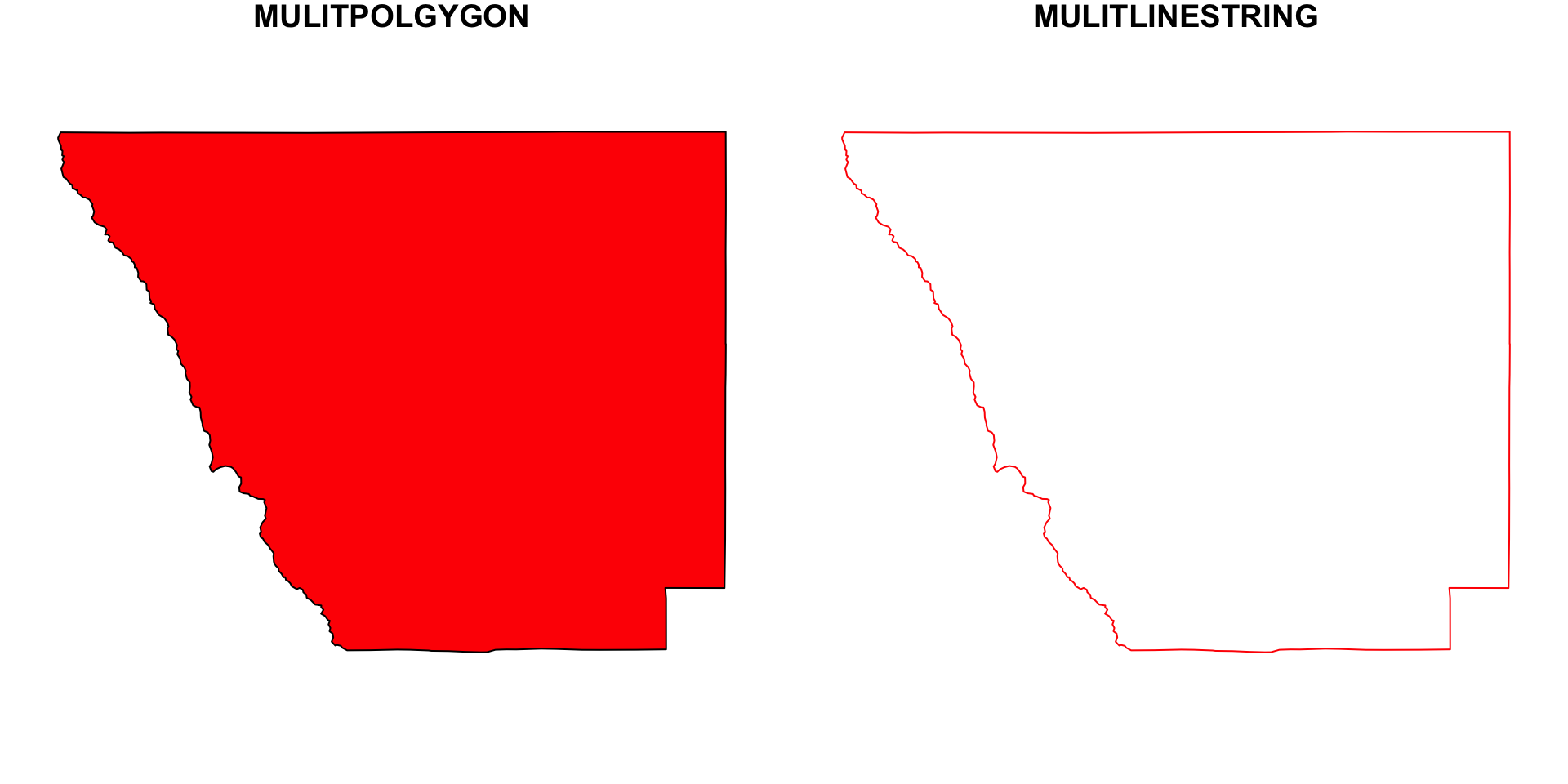
(co1 = AOI::aoi_get(state = "CO", county = "Larimer")$geometry)
#> Geometry set for 1 feature
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -106.1954 ymin: 40.25778 xmax: -104.9431 ymax: 40.99844
#> Geodetic CRS: WGS 84
#> MULTIPOLYGON (((-105.6533 40.26046, -105.6094 4...
(co_ls = st_cast(co1, "MULTILINESTRING"))
#> Geometry set for 1 feature
#> Geometry type: MULTILINESTRING
#> Dimension: XY
#> Bounding box: xmin: -106.1954 ymin: 40.25778 xmax: -104.9431 ymax: 40.99844
#> Geodetic CRS: WGS 84
#> MULTILINESTRING ((-105.6533 40.26046, -105.6094...Lecture 24
Measures, Predicates, and the DE-9IM
Jumping back in …
- In the last lecture we learned about the
sfpackage and how it relates to the broader spatial ecosystem - We also learned about the
sfobject and how it is a data.frame with a geometry column.
Conversion between types
Lets take the Larimer County as our sf object…
Level of Feature
- The level of the feature is the level of the geometry.
1 LINESTRING (sfg) to 1 POINT (sfg)
. . .
1 LINESTRING (sfc) to POINT set (sfc)
In Reverse …
4 POINTs (sfc) to 4 LINESTRING (sfc)
1 MULTIPOINT POINT (sfc) to 1 LINESTRING (sfc)
Disolving Geometries Boundaries
Combining geometries preserves their interior boundaries, unioning dissolves the internal boundaries:
(co_geom = co$geometry)
#> Geometry set for 64 features
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS: WGS 84
#> First 5 geometries:
#> MULTIPOLYGON (((-105.0532 39.79106, -104.976 39...
#> MULTIPOLYGON (((-105.4855 37.5779, -105.4859 37...
#> MULTIPOLYGON (((-103.7065 39.73989, -103.7239 3...
#> MULTIPOLYGON (((-107.1287 37.42294, -107.2803 3...
#> MULTIPOLYGON (((-102.0416 37.64428, -102.0558 3...


Spatial Data Science …
Reading and writing (I/O)
As we’ve seen above, reading spatial data from an external file can be done via sf
Writing takes place in the same fashion, using write_sf:
From Tables (e.g. CSV)
Spatial data can also be created from CSV and other flat files once it is in R:
(cities = read_csv("../labs/data/uscities.csv") |>
select(city, state_name, county_name, population, lat, lng) )
#> # A tibble: 31,254 × 6
#> city state_name county_name population lat lng
#> <chr> <chr> <chr> <dbl> <dbl> <dbl>
#> 1 New York New York Queens 18832416 40.7 -73.9
#> 2 Los Angeles California Los Angeles 11885717 34.1 -118.
#> 3 Chicago Illinois Cook 8489066 41.8 -87.7
#> 4 Miami Florida Miami-Dade 6113982 25.8 -80.2
#> 5 Houston Texas Harris 6046392 29.8 -95.4
#> 6 Dallas Texas Dallas 5843632 32.8 -96.8
#> 7 Philadelphia Pennsylvania Philadelphia 5696588 40.0 -75.1
#> 8 Atlanta Georgia Fulton 5211164 33.8 -84.4
#> 9 Washington District of Columbia District of Columb… 5146120 38.9 -77.0
#> 10 Boston Massachusetts Suffolk 4355184 42.3 -71.1
#> # ℹ 31,244 more rowsTo do this, you must specify the X and the Y coordinate columns as well as a CRS:
- A typical lat/long CRS is EPSG:4326
(cities_sf <- st_as_sf(cities, coords = c("lng", "lat"), crs = 4326))
#> Simple feature collection with 31254 features and 4 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -176.6295 ymin: 17.9559 xmax: 174.111 ymax: 71.2727
#> Geodetic CRS: WGS 84
#> # A tibble: 31,254 × 5
#> city state_name county_name population geometry
#> * <chr> <chr> <chr> <dbl> <POINT [°]>
#> 1 New York New York Queens 18832416 (-73.9249 40.6943)
#> 2 Los Angeles California Los Angeles 11885717 (-118.4068 34.1141)
#> 3 Chicago Illinois Cook 8489066 (-87.6866 41.8375)
#> 4 Miami Florida Miami-Dade 6113982 (-80.2101 25.784)
#> 5 Houston Texas Harris 6046392 (-95.3885 29.786)
#> 6 Dallas Texas Dallas 5843632 (-96.7667 32.7935)
#> 7 Philadelphia Pennsylvania Philadelph… 5696588 (-75.1339 40.0077)
#> 8 Atlanta Georgia Fulton 5211164 (-84.422 33.7628)
#> 9 Washington District of Co… District o… 5146120 (-77.0163 38.9047)
#> 10 Boston Massachusetts Suffolk 4355184 (-71.0852 42.3188)
#> # ℹ 31,244 more rowsData Manipulation
Since
sfobjects aredata.frames, ourdplyrverbs work!Lets find the most populous city in each Colorado county…
sf and dplyr
#> Simple feature collection with 31254 features and 4 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -176.6295 ymin: 17.9559 xmax: 174.111 ymax: 71.2727
#> Geodetic CRS: WGS 84
#> # A tibble: 31,254 × 5
#> city state_name county_name population geometry
#> * <chr> <chr> <chr> <dbl> <POINT [°]>
#> 1 New York New York Queens 18832416 (-73.9249 40.6943)
#> 2 Los Angeles California Los Angeles 11885717 (-118.4068 34.1141)
#> 3 Chicago Illinois Cook 8489066 (-87.6866 41.8375)
#> 4 Miami Florida Miami-Dade 6113982 (-80.2101 25.784)
#> 5 Houston Texas Harris 6046392 (-95.3885 29.786)
#> 6 Dallas Texas Dallas 5843632 (-96.7667 32.7935)
#> 7 Philadelphia Pennsylvania Philadelph… 5696588 (-75.1339 40.0077)
#> 8 Atlanta Georgia Fulton 5211164 (-84.422 33.7628)
#> 9 Washington District of Co… District o… 5146120 (-77.0163 38.9047)
#> 10 Boston Massachusetts Suffolk 4355184 (-71.0852 42.3188)
#> # ℹ 31,244 more rowssf and dplyr
#> Simple feature collection with 477 features and 4 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -109.0066 ymin: 37.0155 xmax: -102.0804 ymax: 40.9849
#> Geodetic CRS: WGS 84
#> # A tibble: 477 × 5
#> city state_name county_name population geometry
#> * <chr> <chr> <chr> <dbl> <POINT [°]>
#> 1 Denver Colorado Denver 2691349 (-104.8758 39.762)
#> 2 Colorado Springs Colorado El Paso 638421 (-104.7605 38.8674)
#> 3 Aurora Colorado Arapahoe 390201 (-104.7237 39.7083)
#> 4 Fort Collins Colorado Larimer 339256 (-105.0656 40.5477)
#> 5 Lakewood Colorado Jefferson 156309 (-105.1172 39.6977)
#> 6 Greeley Colorado Weld 143554 (-104.7706 40.4152)
#> 7 Thornton Colorado Adams 142878 (-104.9438 39.9197)
#> 8 Grand Junction Colorado Mesa 141008 (-108.5673 39.0877)
#> 9 Arvada Colorado Jefferson 122835 (-105.151 39.832)
#> 10 Boulder Colorado Boulder 120121 (-105.2524 40.0248)
#> # ℹ 467 more rowssf and dplyr
#> Simple feature collection with 477 features and 4 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -109.0066 ymin: 37.0155 xmax: -102.0804 ymax: 40.9849
#> Geodetic CRS: WGS 84
#> # A tibble: 477 × 5
#> # Groups: county_name [64]
#> city state_name county_name population geometry
#> <chr> <chr> <chr> <dbl> <POINT [°]>
#> 1 Denver Colorado Denver 2691349 (-104.8758 39.762)
#> 2 Colorado Springs Colorado El Paso 638421 (-104.7605 38.8674)
#> 3 Aurora Colorado Arapahoe 390201 (-104.7237 39.7083)
#> 4 Fort Collins Colorado Larimer 339256 (-105.0656 40.5477)
#> 5 Lakewood Colorado Jefferson 156309 (-105.1172 39.6977)
#> 6 Greeley Colorado Weld 143554 (-104.7706 40.4152)
#> 7 Thornton Colorado Adams 142878 (-104.9438 39.9197)
#> 8 Grand Junction Colorado Mesa 141008 (-108.5673 39.0877)
#> 9 Arvada Colorado Jefferson 122835 (-105.151 39.832)
#> 10 Boulder Colorado Boulder 120121 (-105.2524 40.0248)
#> # ℹ 467 more rowssf and dplyr
#> Simple feature collection with 64 features and 4 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -108.9071 ymin: 37.1751 xmax: -102.2627 ymax: 40.9849
#> Geodetic CRS: WGS 84
#> # A tibble: 64 × 5
#> # Groups: county_name [64]
#> city state_name county_name population geometry
#> <chr> <chr> <chr> <dbl> <POINT [°]>
#> 1 Thornton Colorado Adams 142878 (-104.9438 39.9197)
#> 2 Alamosa Colorado Alamosa 9847 (-105.877 37.4752)
#> 3 Aurora Colorado Arapahoe 390201 (-104.7237 39.7083)
#> 4 Pagosa Springs Colorado Archuleta 1718 (-107.0307 37.2675)
#> 5 Springfield Colorado Baca 1482 (-102.6189 37.405)
#> 6 Las Animas Colorado Bent 2480 (-103.2236 38.0695)
#> 7 Boulder Colorado Boulder 120121 (-105.2524 40.0248)
#> 8 Broomfield Colorado Broomfield 75110 (-105.0526 39.9542)
#> 9 Salida Colorado Chaffee 5786 (-105.9979 38.5298)
#> 10 Cheyenne Wells Colorado Cheyenne 949 (-102.3521 38.8192)
#> # ℹ 54 more rowssf and dplyr
Plotting
We’ve already seen that
ggplot()is a powerful visualization tool:- canvas
- layers (geoms)
- labels
- facets
- themes
spatial work in R is becoming so common that
ggplot()comes with a sf geom (geom_sf)
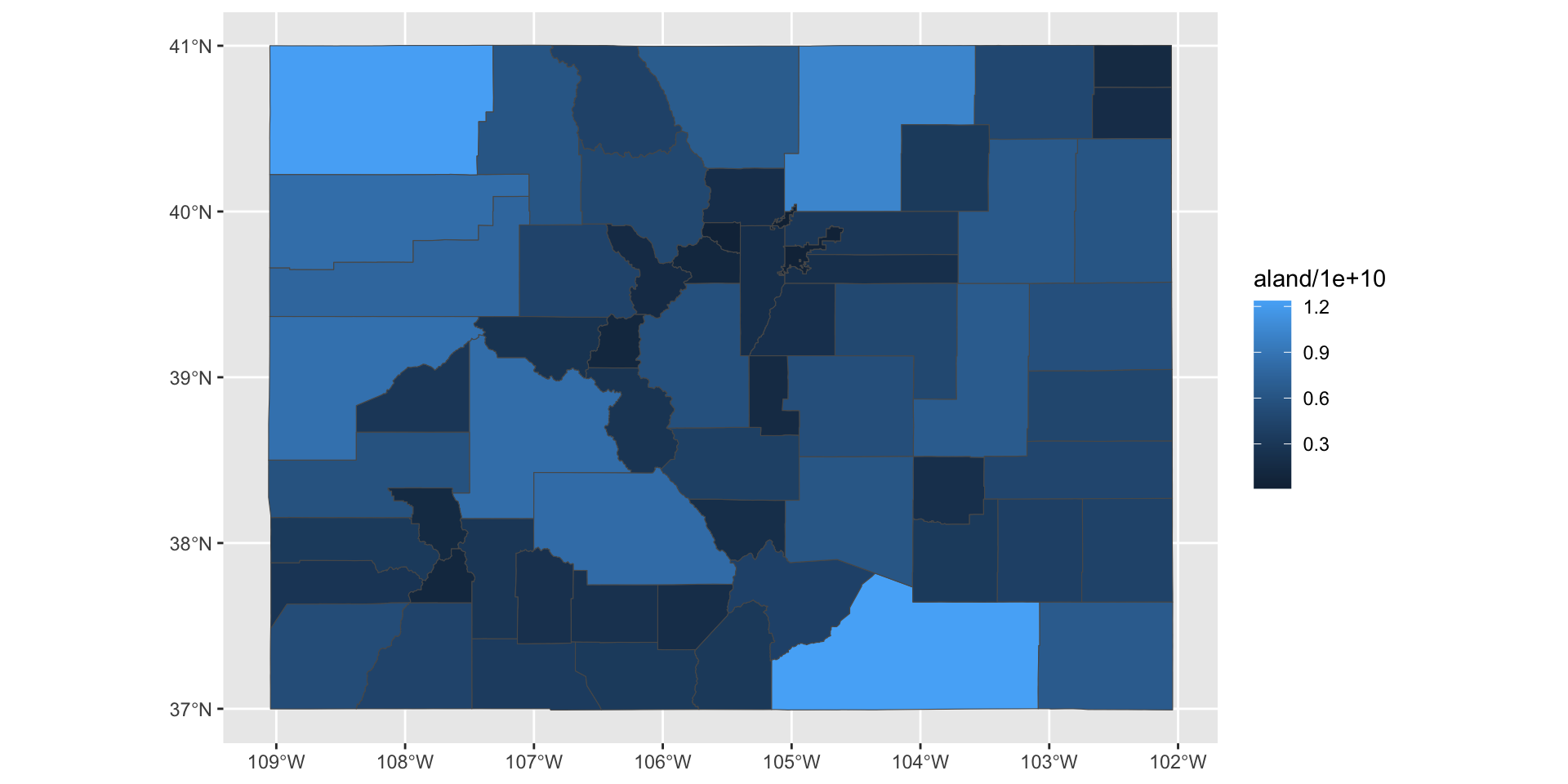
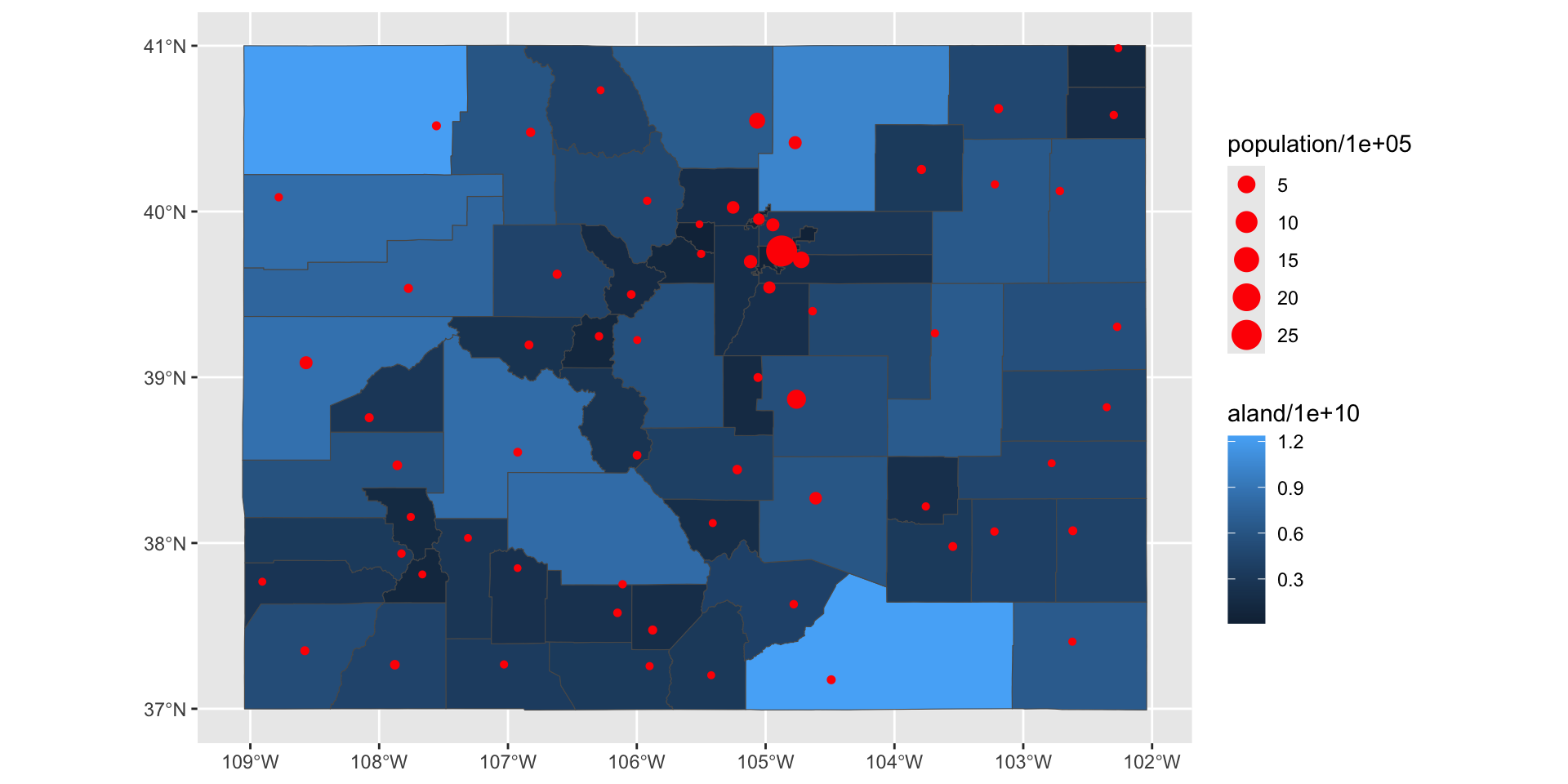
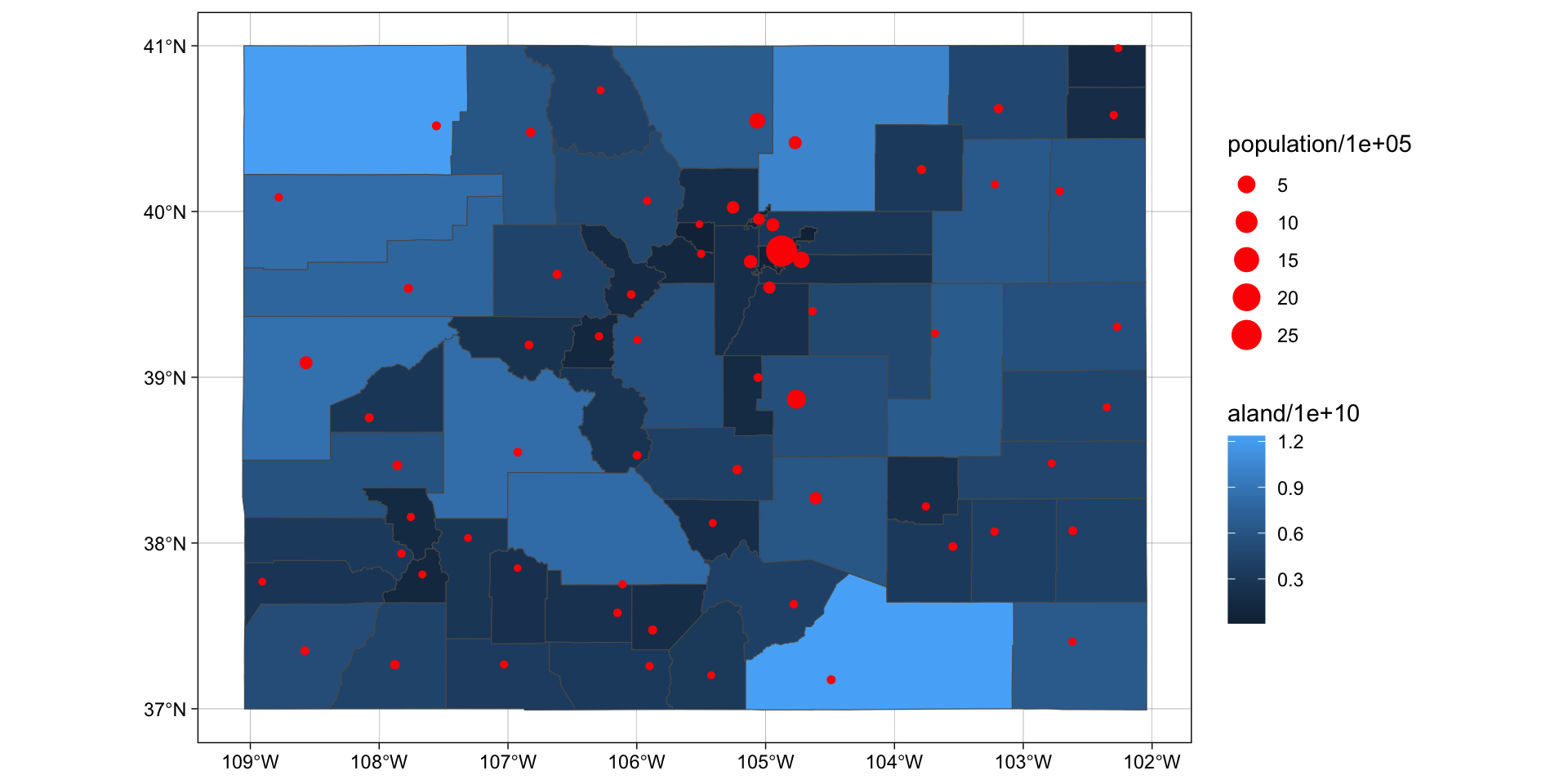
sf an ggplot
sf an ggplot
sf an ggplot
sf an ggplot
sf an ggplot
Spatial Sampling
- Spatial sampling is a common task in spatial data science.
Like
rsample,spatialsampleprovides building blocks for creating and analyzing resamples of a spatial data set but does not include code for modeling or computing statistics.
The stickness of sfc column
- Geometry columns are “sticky” meaning they persist through data manipulation:
co |>
select(name) |>
slice(1:2)
#> Simple feature collection with 2 features and 1 field
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -106.0393 ymin: 37.3562 xmax: -103.7057 ymax: 40.00137
#> Geodetic CRS: WGS 84
#> # A tibble: 2 × 2
#> name geometry
#> <chr> <MULTIPOLYGON [°]>
#> 1 Adams (((-105.0532 39.79106, -105.0532 39.86362, -105.0529 39.91422, -105.0…
#> 2 Alamosa (((-105.4855 37.5779, -105.4907 37.57546, -105.4961 37.57006, -105.49…- Dropping the geometry column requires dropping the geometry via
sf:
- Or cohersing the
sfobject to adata.frame:
Coordinate Systems: What makes spatial data spatial?
- What makes a feature geometry spatial is the reference system…
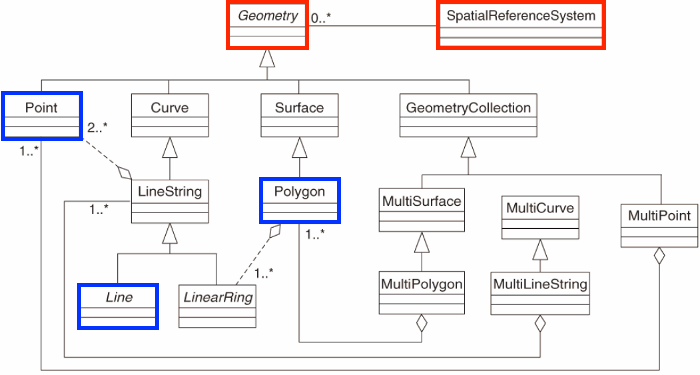
Coordinate Systems
Coordinate Reference Systems (CRS) define how spatial features relate to the surface of the Earth.
CRSs are either geographic or projected…
CRSs are measurement units for coordinates…
sf tools
In sf we have three tools for exploring, define, and changing CRS systems:
st_crs : Retrieve coordinate reference system from sf or sfc object
st_set_crs : Set or replace coordinate reference system from object
st_transform : Transform or convert coordinates of simple feature
Again, “st” (like PostGIS) denotes it is an operation that can work on a ” s patial t ype”
Geographic Coordinate Systms (GCS)
A GCS identifies locations on the curved surface of the earth.
Locations are measured in angular units from the center of the earth relative to the plane defined by the equator and the plane defined by the prime meridian.
The vertical angle describes the latitude and the horizontal angle the longitude
In most coordinate systems, the North-South and East-West directions are encoded as +/-.
North and East are positive (
+) and South and West are negative (-) sign.
Geographic Coordinate Systms (GCS)
A GCS is defined by 3 mathematical models of the earth’s shape:
- an ellipsoid: earth’s surface that is smooth
- defined by two radii: semi-major and semi-minor axes
- a geoid: earth’s surface that is undulating
- defined by the gravitational potential of the earth
- a datum: earth’s surface that is aligned to the geoid
- defined by the alignment of the ellipsoid to the geoid
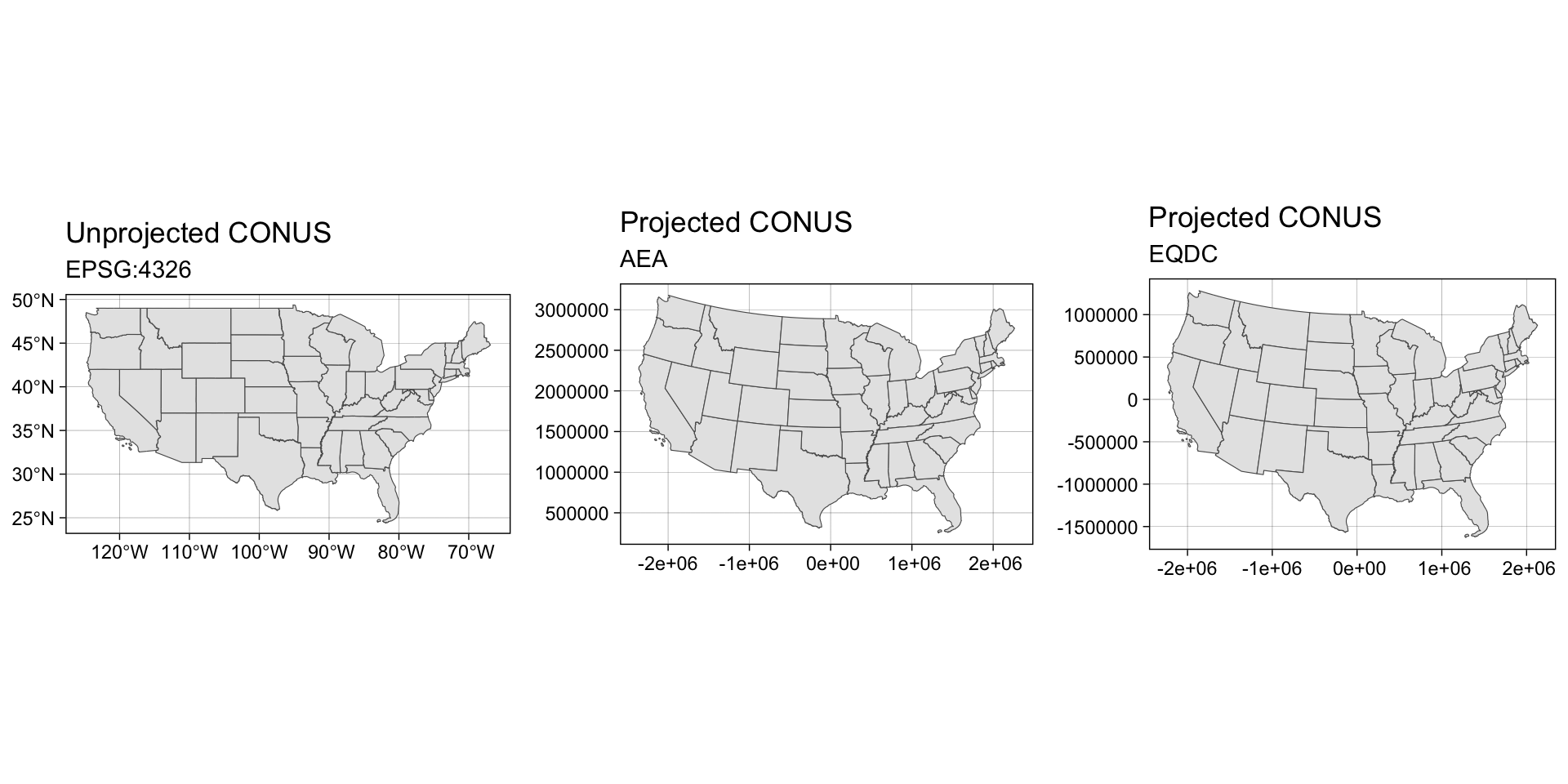
Projected Coordinate Systems (PCS)
The surface of the earth is curved but maps (and to data GIS) is flat.
Projected coordinate systems have an origin, an x axis, a y axis, and a linear unit of measure.
Going from a GCS to a PCS requires mathematical transformations.
There are three main groups of projection types:
- conic:
- defined by a cone touching the earth at 1 or 2 lines of tangency
- best suited for mid-latitude areas
- cylindrical:
- defined by a cylinder touching the earth at 1 or 2 lines of tangency
- best suited for large areas
- planar:
- defined by a plane touching the earth at 1 point or along 1 line of tangency
- best suited for polar regions
- conic:
Spatial Properties
All PCS distort real-world geographic features.
Think about trying to unpeel an orange while preserving the skin
The four spatial properties that are subject to distortion are: shape, area, distance and direction
A map that preserves shape is called
conformal;one that preserves area is called
equal-area;one that preserves distance is called
equidistantone that preserves direction is called
azimuthalEach map projection can preserve only one or two of the four spatial properties.
Often, projections are named after the spatial properties they preserve.
When working with small-scale (large area) maps and when multiple spatial properties are needed, it is best to break the analyses across projections to minimize errors associated with spatial distortion.
Setting CRSs/PCSs
sfc objects have two attributes to store a CRS: epsg and proj4string
proj4stringis a character string that describes the projection and the datum.- This is a standard way to describe projections, but it is not always easy to read or understand.
epsgis an integer ID for a known CRS that can be resolved into aproj4string.- This is somewhat equivalent to the idea that a 6-digit FIP code can be resolved to a state/county pair
Transform and retrive
So …
They can be geographic (3D, angular units)
Ellipsoid (squished sphere model)
geoid (mathematical model of gravitational field)
datum marks the relationship between the ellipsoid and geoid
can be local (NAD27)
can be global (WGS84, NAD83)
So …
CRSs can be projected (x-y axis, measurement units (m), false origin)
All PCS are based on GCS
Projections seek to place the 3D earth on 2D
Does this by defining a plane that can be conic, cylindrical or planar
“unfolding to this plane” creates distortion of shape, area, distance, or direction
The distortion is greater from point/lines of tangency or secanacy
But …
In all cases, CRS’s place geoemtries, linked to data, on the earths surface in a way they can be related, measured, and analyzed….
Measures (GEOS Measures)
Measures are the questions we ask about the dimension of a geometry
How long is a line or polygon perimeter (unit)
What is the area of a polygon (unit2)
How far are two object from one another (unit)
Measures come from the GEOS library
Measures are in the units of the base projection
Measures can be Euclidean or geodesic
geodesic (Great Circle) distances can be more accurate by eliminating distortion
but are much slower to calculate
For example …
Units
When possible measure operations report results with a units appropriate for the CRS:
co <- st_read("data/co.shp")
#> Reading layer `co' from data source
#> `/Users/mikejohnson/github/csu-ess-330/slides/data/co.shp'
#> using driver `ESRI Shapefile'
#> Simple feature collection with 64 features and 4 fields
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -109.0602 ymin: 36.99246 xmax: -102.0415 ymax: 41.00342
#> Geodetic CRS: WGS 84
a <- st_area(co[1,])
attributes(a) |> unlist()
#> units.numerator1 units.numerator2 class
#> "m" "m" "units"The units package can be used to convert between units:
and the results can be stripped of their attributes for cases where numeric values are needed (e.g. math operators and ggplot):
Assignment
The process of finding, downloading and accessing data is the first step of every analysis. Here we will go through these steps.
First go to this site and download the appropriate (free) dataset into the data directory of your project.
Once downloaded, read it into your working session using
readr::read_csv()and explore the dataset until you are comfortable with the information it contains.While this data has everything we want, it is not yet spatial. Convert the
data.frameto a spatial object usingst_as_sfand prescribing the coordinate variables and CRS (Hint what projection are the raw coordinates in?)
Assignment
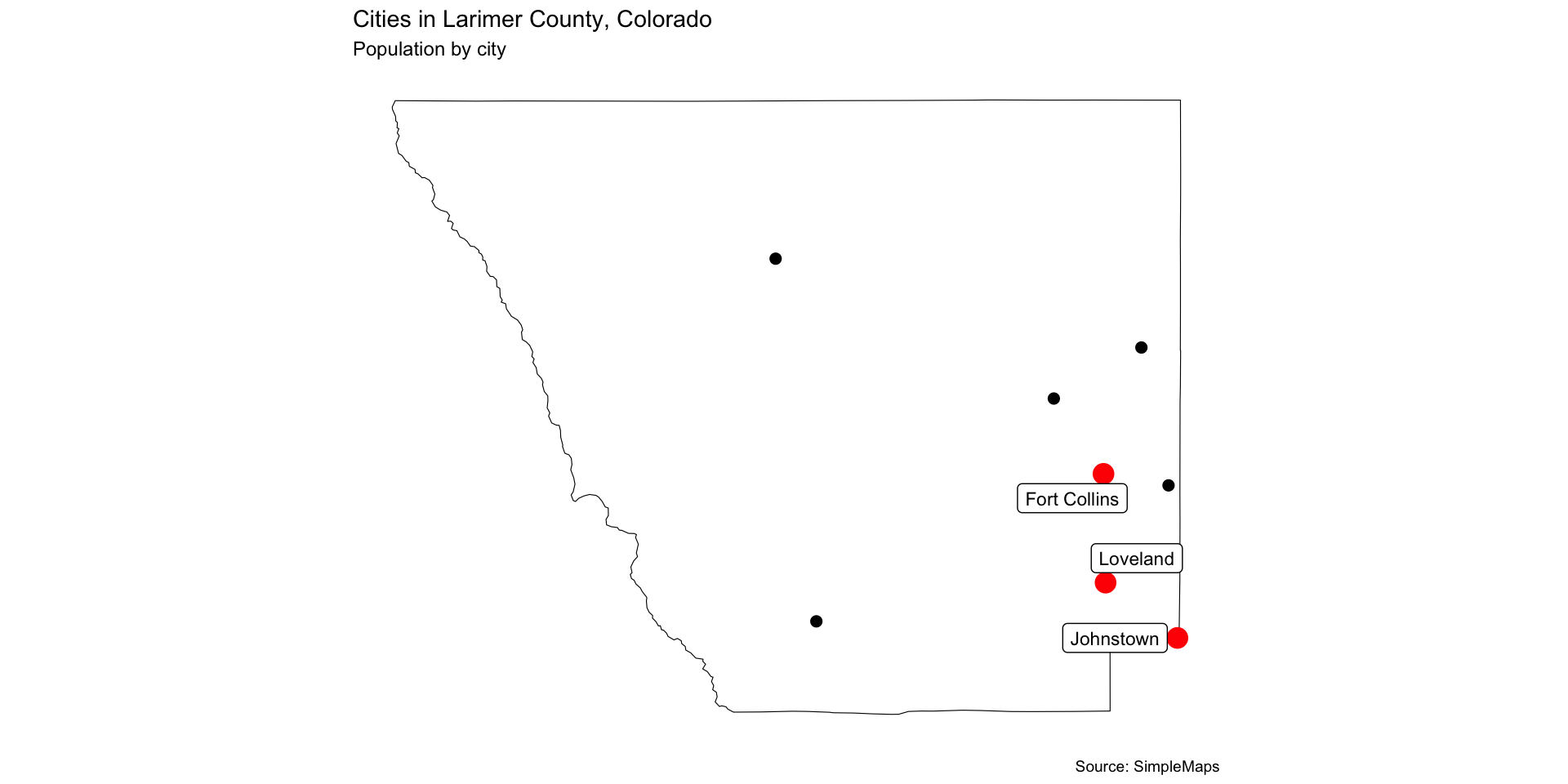
Next, we will find the county boundaries for Larimer County, Colorado. Use the
aoi_get(state = "CO", county = "Larimer")function to get the county boundary.Use
st_filterto find all the cities in the dataset that are within Larimer County.Plot the cities and the county boundary on a single map. Use
geom_sf()to plot both layers and make sure to set thefillandcolorarguments appropriately.Next, determine the three cities in Larimer County with the highest population and add these to the map. Use a larger point size and a different color for the points will help them stand out.
Assignment
Last, you will learn a new approach for labeling things on a ggplot that is particularly useful for cartography….
If you dont already have it, install the
ggrepelpackage. This package provides a function calledgeom_label_repel()that will help you label the points without overlapping labels. The syntax is similar togeom_label()but it will automatically adjust the position of the labels to avoid overlap.Like all
ggplot2layers, you can add this to your existing plot and first must prescribe the data to be used.In the aesthetic mapping, you will need to specify the
labelargument to be the name of the city. and thegeometryargument to be the geometry column of you sf object.Finally, you need to set the
statargument tosf_coordinatesso the function knows to use the coordinates of the geometry column for the label positions.
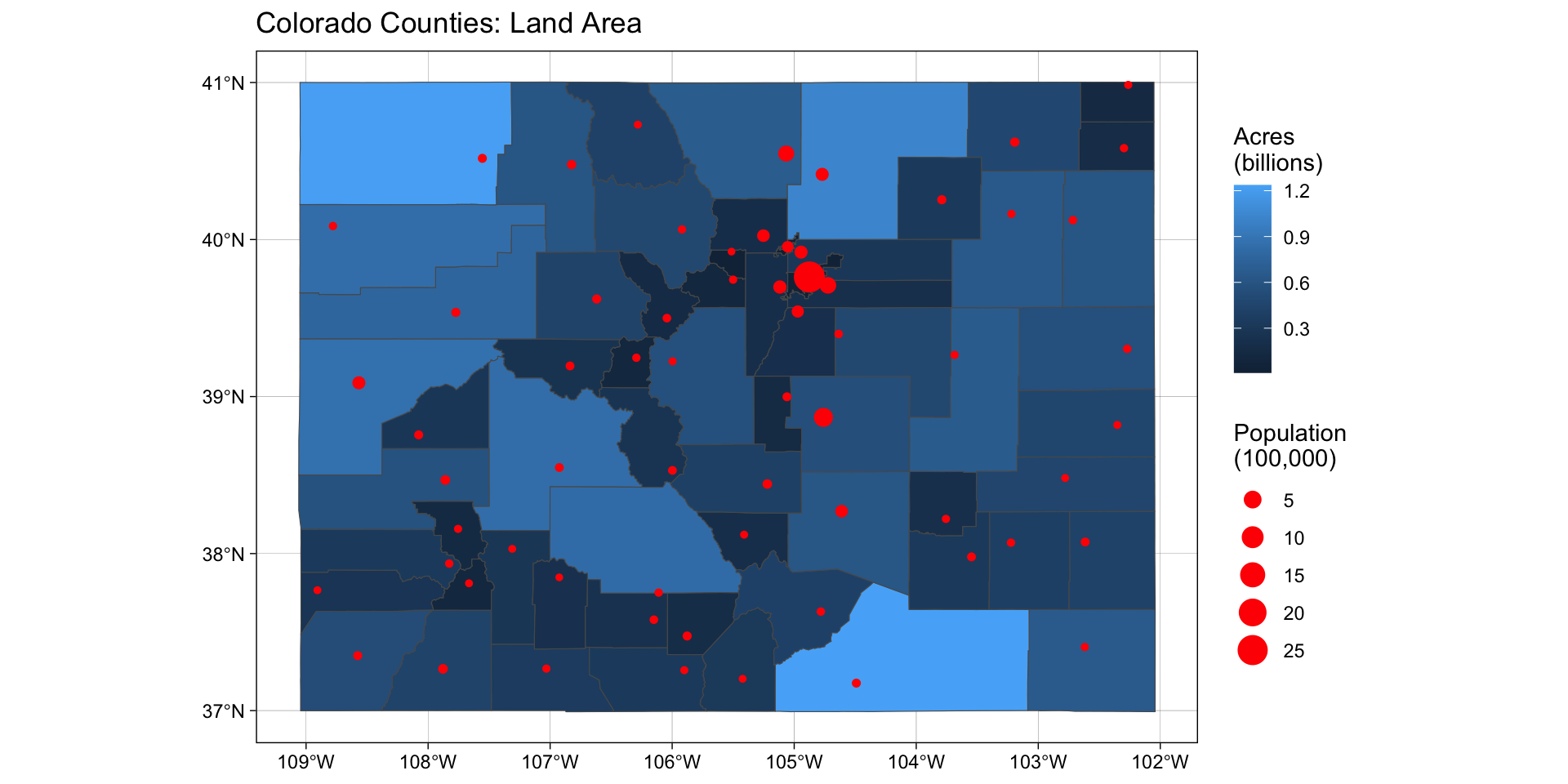
Assignment
Your final map should look something like this (with design elements of your choosing):
Use ggsave to save your final map to the images directory of your project and submit the PNG to Canvas.