Lecture 25

Predicates and the DE-9IM

Announcements

Vector Data Lab: Due this week
Lab Next Week: Lightning Talks, In Person (efficivly your final lab assignment)

Final Report Due: May 14th, 2025 5PM
Credit Statement: Due with Final Report

No more late work accepted after May 9th, 2025 5PM
All regrades and late work will be updated by this Friday May 2nd, 2025 5PM

Announcements

Current grade breakdown is as follows: A (50%), B (20%), C (11%), D (4%), and F (15%).

There are 2 labs (vector + presentations), the 20% project, and 10% extra credit still remaining.
Reminder: The extra credit is to compile all of your labs into you personal webpage (complete with image and description). This is due May 14th, 2025 5PM as well.

Jumping back in …

Last week we learned about simple features, CRS’s, and the sf package.
We coverd how the sf package fits within the tidyverse data science framework, while adding spatial capabilities.
Some of the first spatial priciples we covered were measures (st_area, st_length, st_distance) and their relation geometry types (POINT, LINESTRING, POLYGON, etc.) and CRSs.
Today, we will cover the DE-9IM model and how it can be used to describe the spatial relationships between geometries…

Predicates

Topologic Diminsions

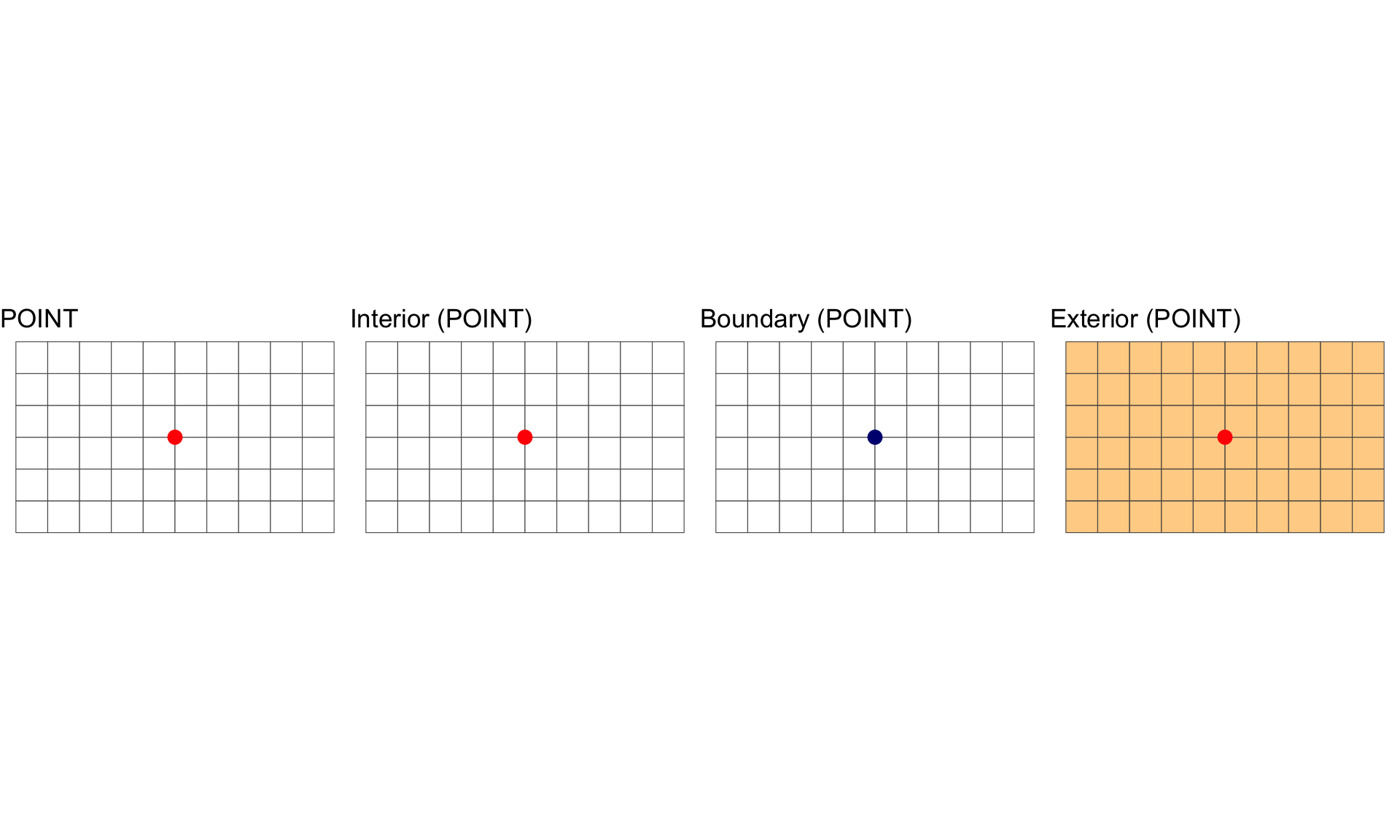
A POINT is shape with a dimension of 0 that occupies a single location in coordinate space.

# POINT defined as numeric vector
(st_dimension(st_point(c(0,1))))
#> [1] 0

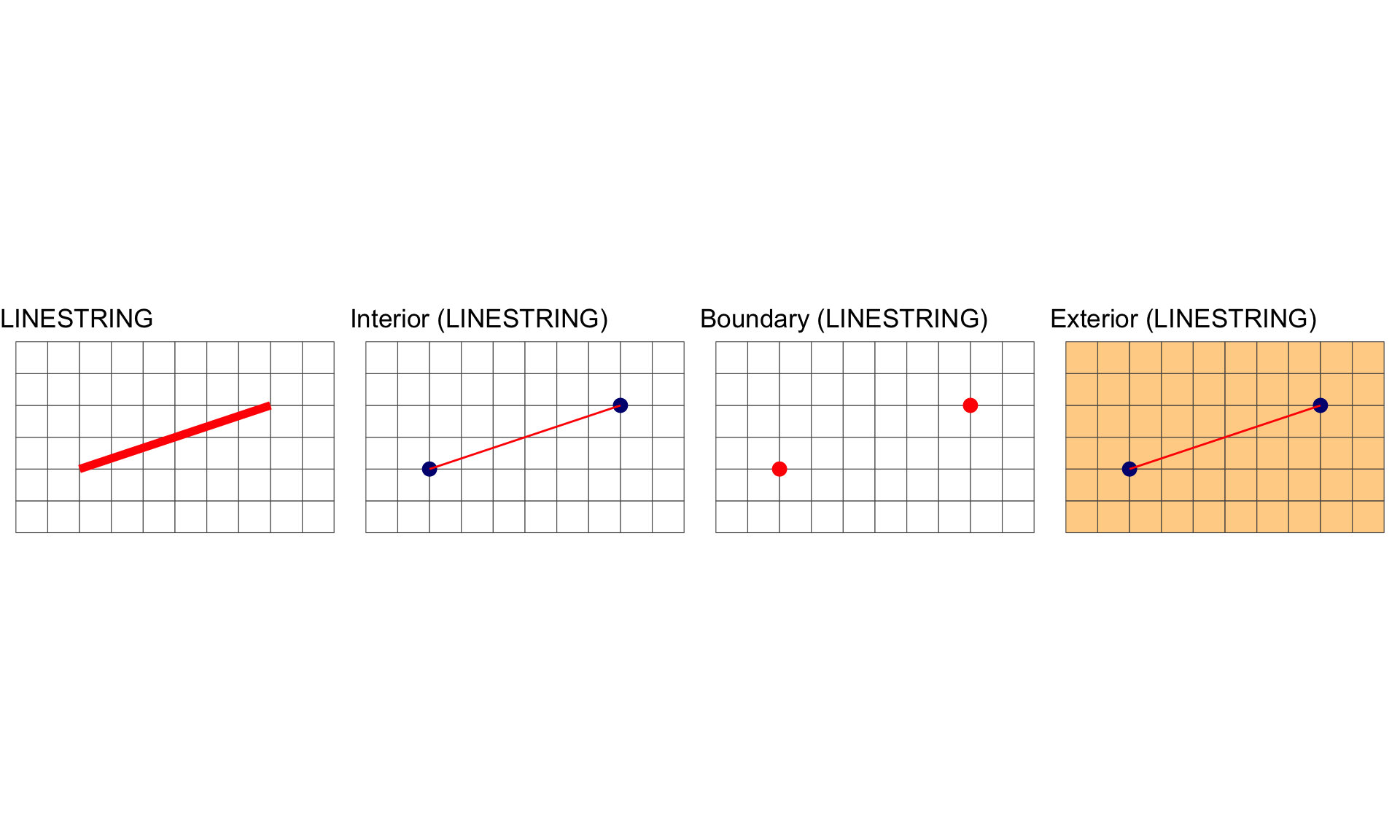
A LINESTRING is shape that has a dimension of 1 (length)

# LINESTRING defined by matrix
(st_dimension(st_linestring(matrix(1:4, nrow = 2))))
#> [1] 1

A POLYGON is surface stored as a list of its exterior and interior rings. It has a dimension of 2. (area)

# POLYGON defined by LIST (interior and exterior rings)
(st_dimension(st_polygon(list(matrix(c(1:4, 1,2), nrow = 3, byrow = TRUE)))))
#> [1] 2

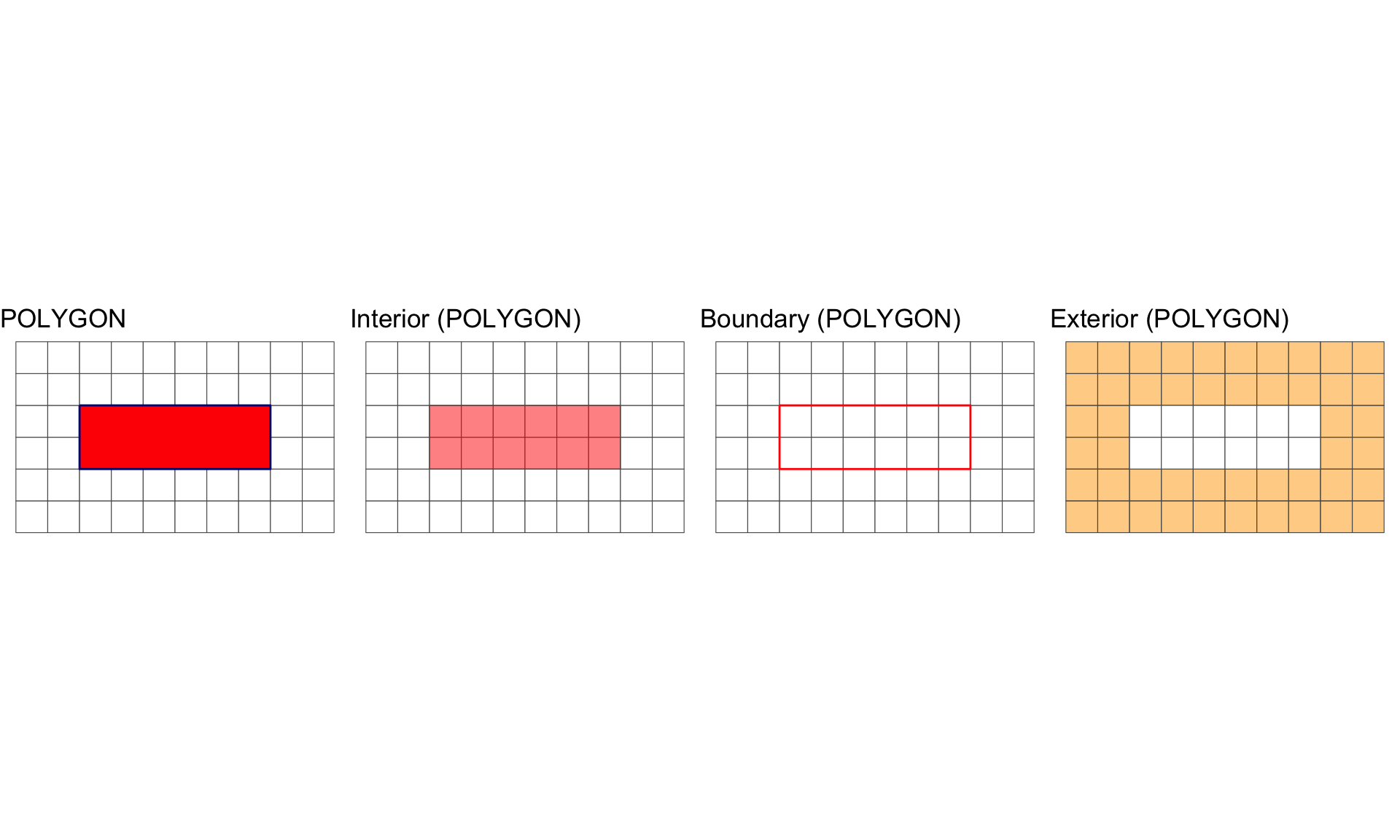
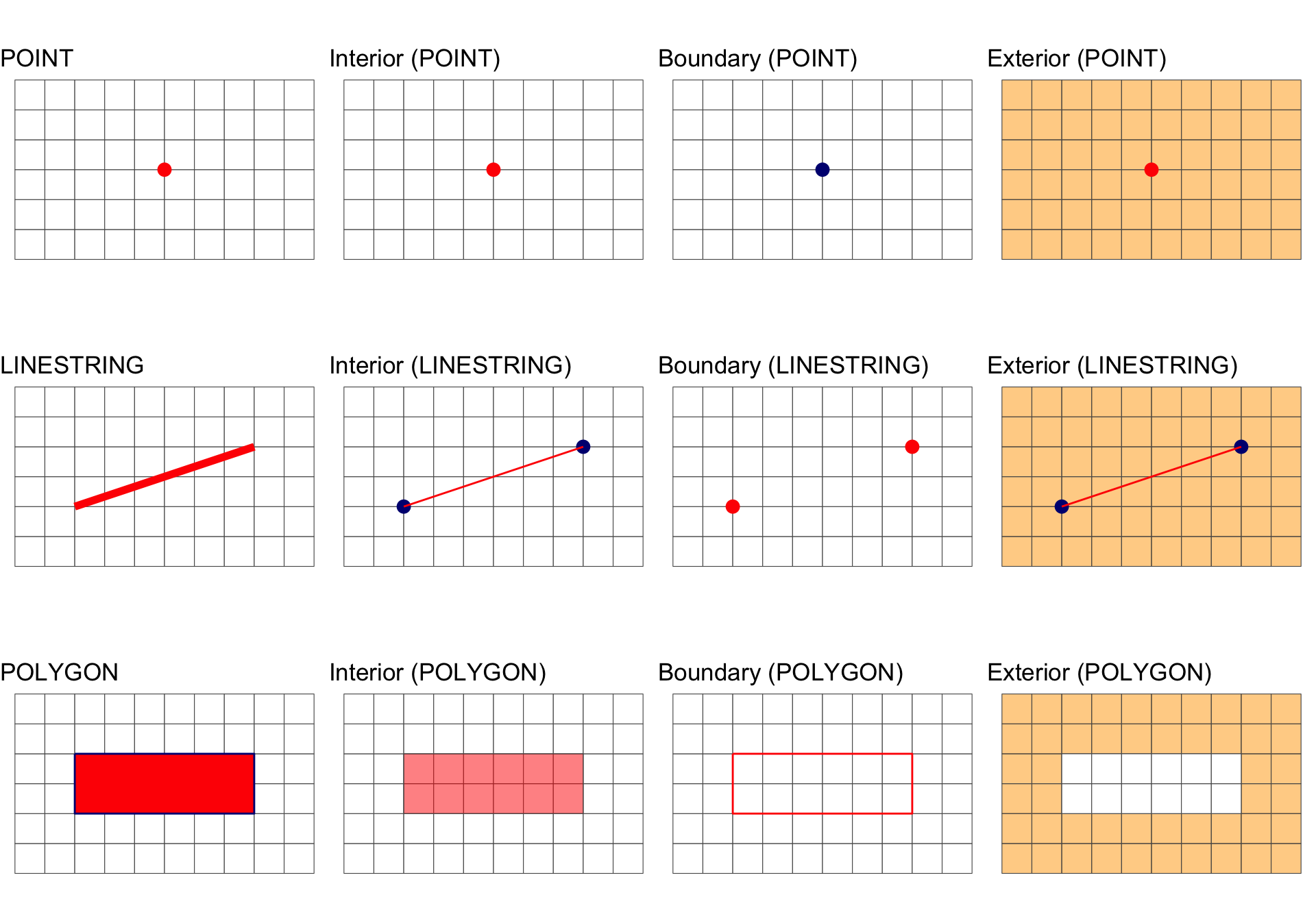
Geometric Interiors, Boundaries and Exteriors

All geometries have interior, boundary and exterior regions.

The terms interior and boundary are used in the context of algebraic topology and manifold theory and not general topology

The OGC has define these states for the common geometry types in the simple features standard:

Dimension	Geometry Type	Interior (I)	Boundary (B)
Point, MultiPoint	0	Point, Points	Empty
LineString, Line	1	Points that are left when the boundary points are removed.	Two end points.
Polygon	2	Points within the rings.	Set of rings.

Interior, Boundary and Exterior: POINTS

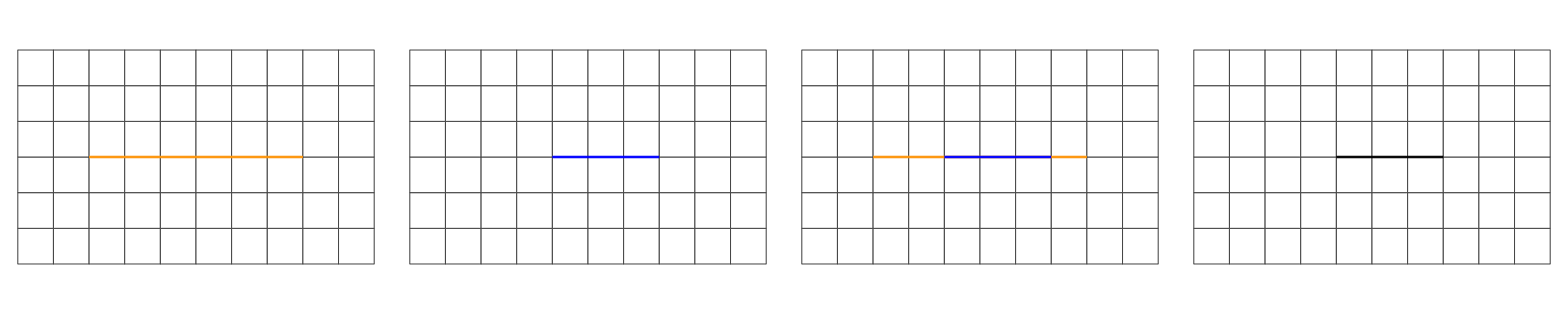
Interior, Boundary and Exterior: LINESTRING

Interior, Boundary and Exterior: POLYGON

Summary

Predicates

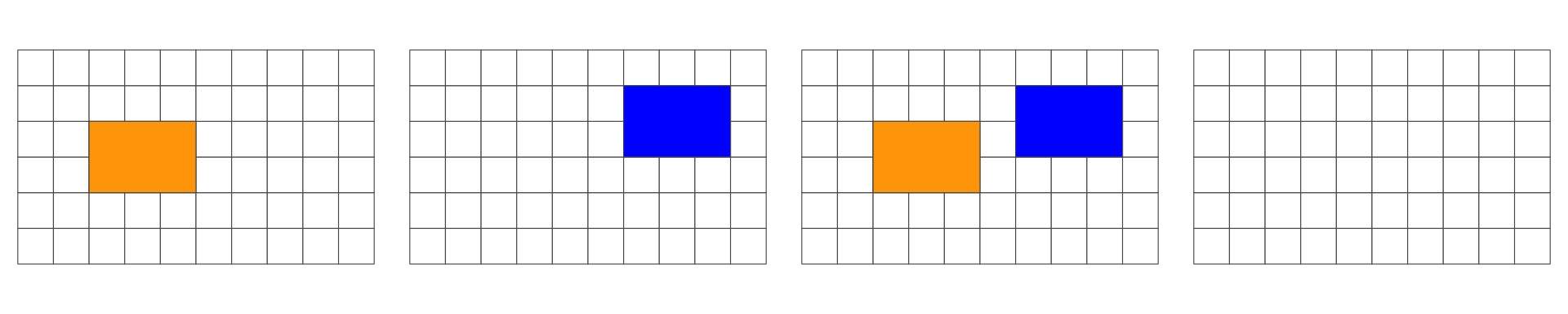
In the following, we are interested in the resulting geometry that occurs when 2 geometries are overlaid…

Overlap is a POINT: 0D

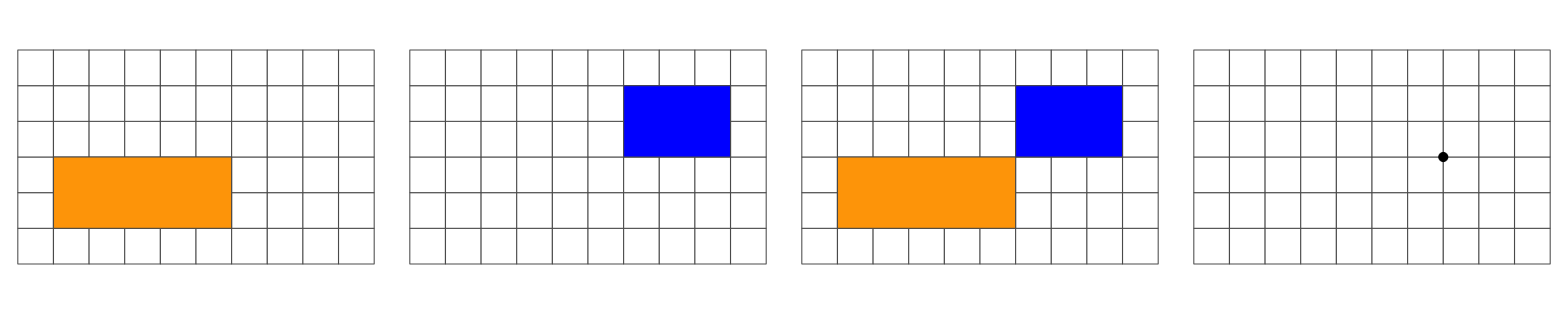
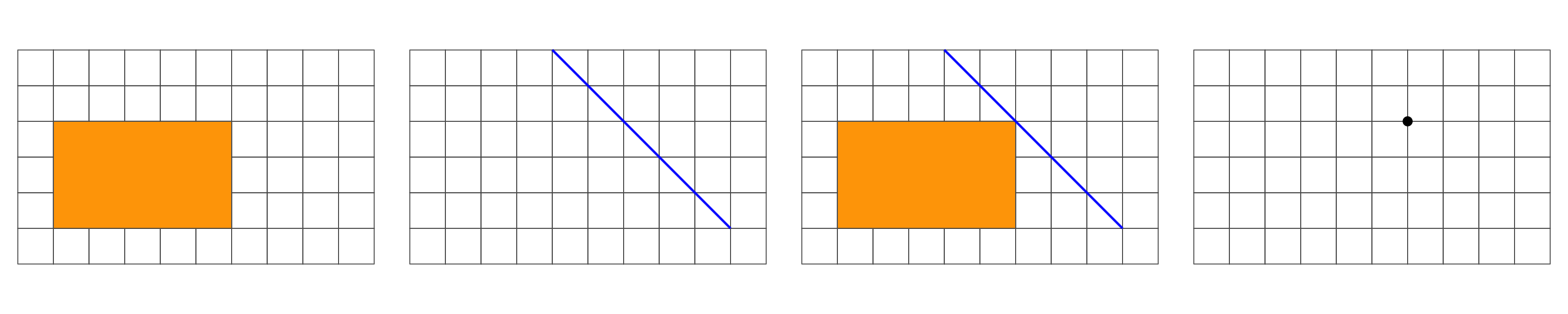
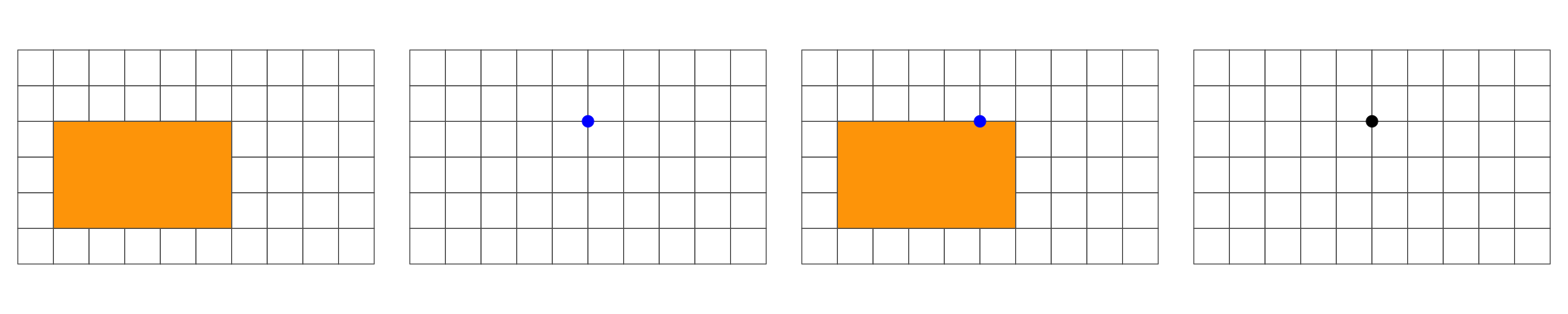
Overlap is a LINESTRING: 1D

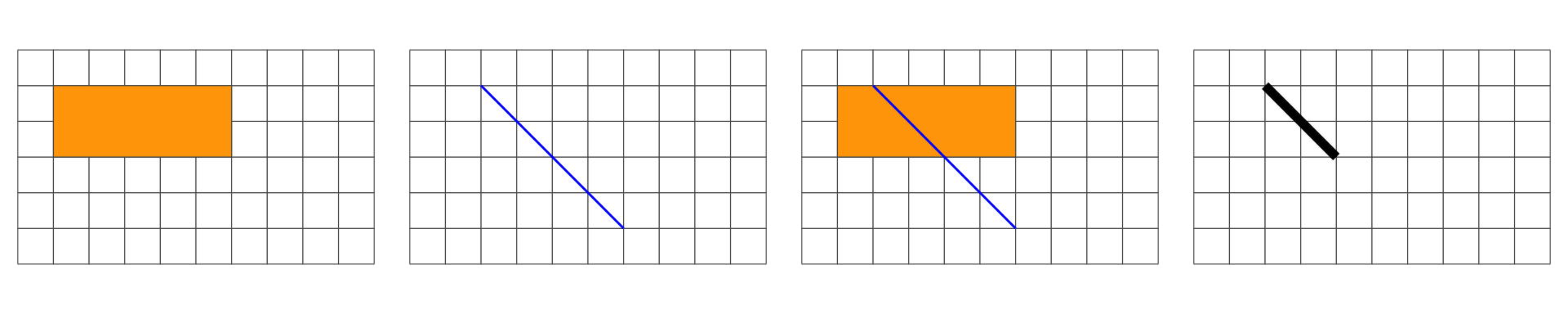
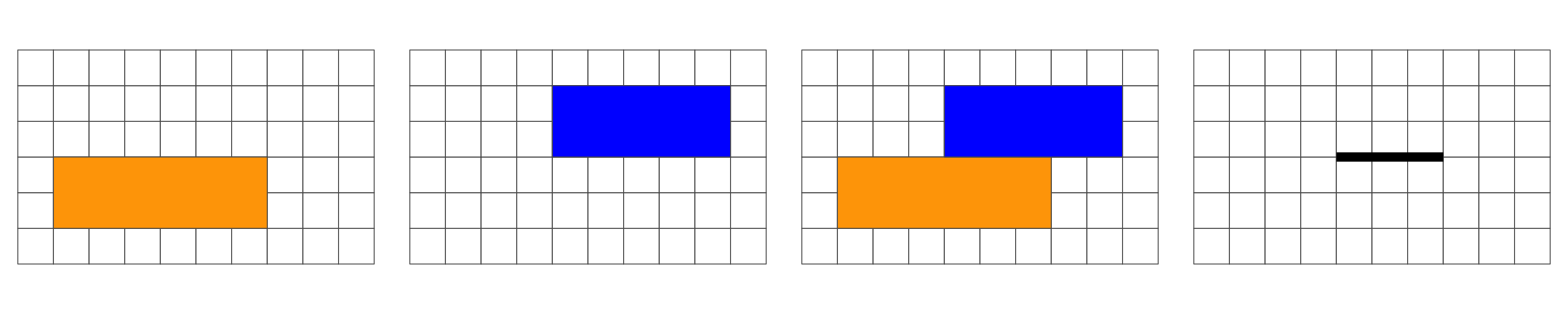
Overlap is a POLYGON: 2D

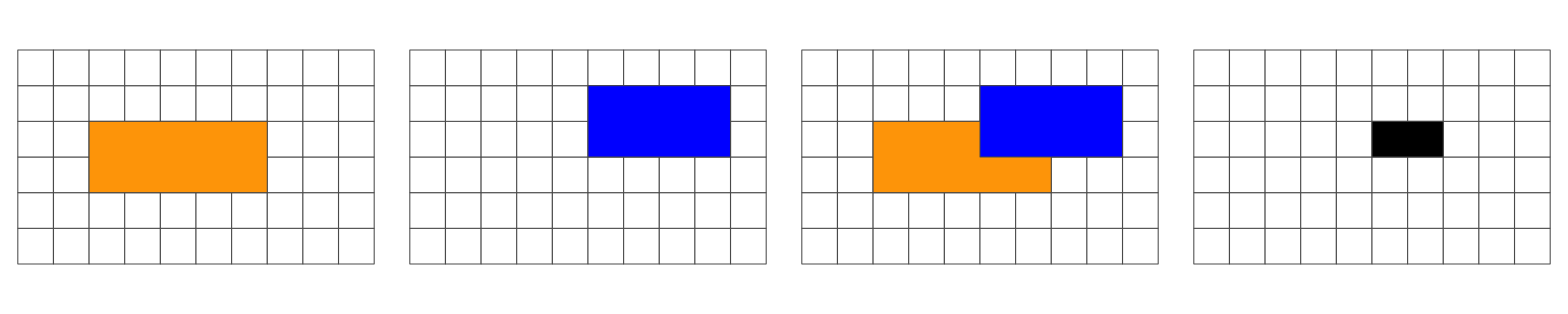
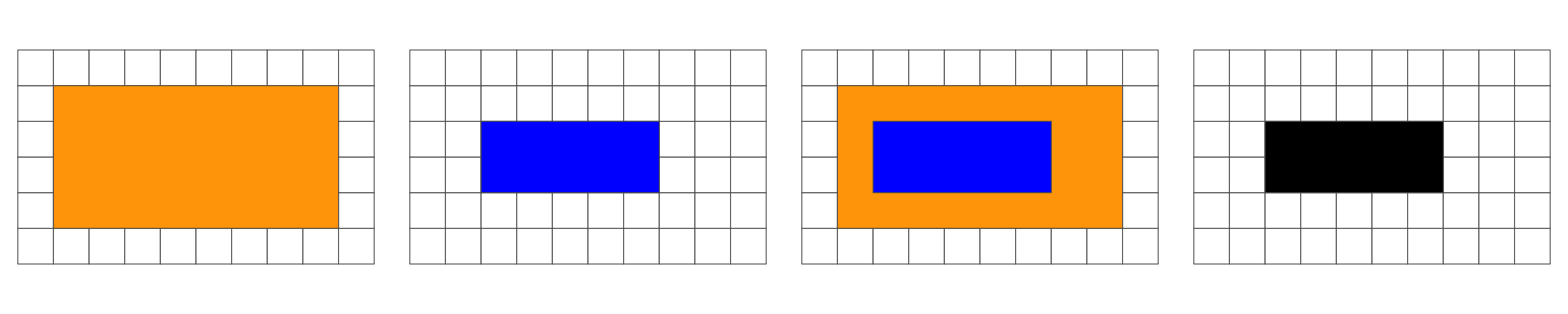
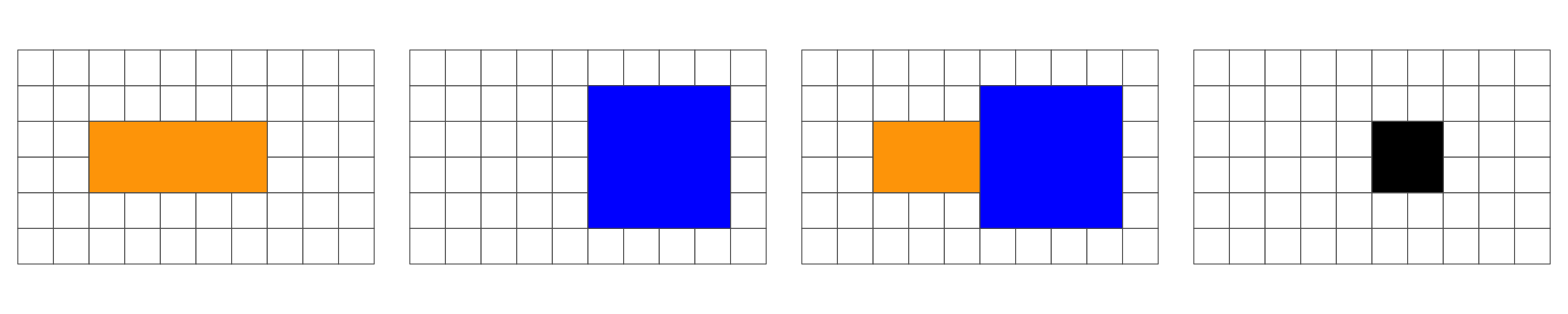
No Overlap = FALSE

Dimensionally Extended 9-Intersection Model

The DE-9IM is a topological model and (standard) used to describe the spatial relations of two geometries
Used in geometry, point-set topology, geospatial topology
The DE-9IM matrix provides a way to classify geometry relations using the set {0,1,2,F} or {T,F}

With a {T,F} matrix domain, there are 512 possible relations ….
About 10 of these, have been given a common name such as intersects, touches, and within.
When testing two geometries against a scheme, the result is a spatial predicate named by the scheme.
Provides the primary basis for queries and assertions in GIS and spatial databases (PostGIS).

The Matrix Model

The DE-9IM matrix is based on a 3x3 intersection matrix:

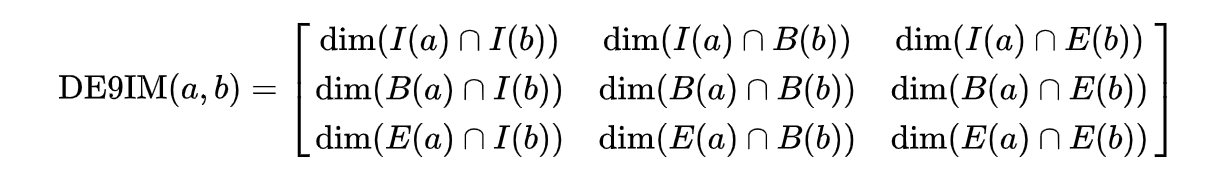
Where:

dim is the dimension of the intersection and
I is the interior
B is the boundary
E is the exterior

Empty sets are denoted as F

non-empty sets are denoted with the maximum dimension of the intersection {0,1,2}

A simpler (binary) version of this matrix can be created by mapping all non-empty intersections {0,1,2} to TRUE.

Where II would state: “Does the Interior of”a” overlaps with the Interior of “b” in a way that produces a point (0), line (1), or polygon (2)”

Where IB would state: “Does the Interior of”a” overlap with the Boundary of “b” in a way that produces a point (0), line (1), or polygon (2)”

Both matrix forms: - dimensional {0,1,2,F} - Boolean {T,F}

Can be serialize as a “DE-9IM string code” representing the matrix in a single string element (standardized format for data interchange)

The OGC has standardized the typical spatial predicates (Contains, Crosses, Intersects, Touches, etc.) as Boolean functions, and the DE-9IM model as a function that returns the DE-9IM code, with domain of {0,1,2,F}

Illustration

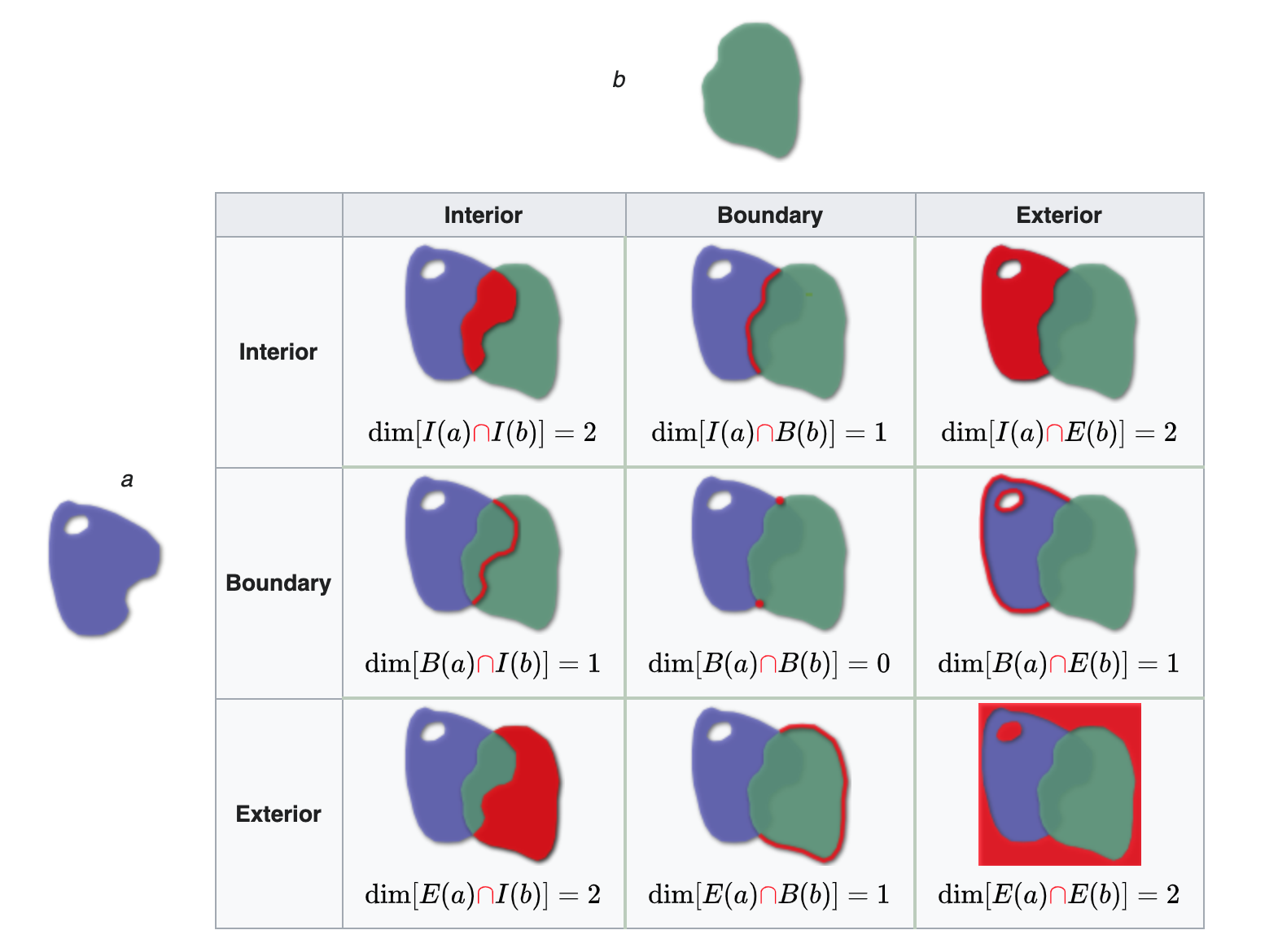
Reading from left-to-right and top-to-bottom, the DE-9IM(a,b) string code is ‘212101212’

Named Predicates

“named spatial predicates” have been defined for some common relations.
A few functions can be derived (expressed by masks) from DE-9IM include (* = wildcard):

Predicate	DE-9IM String Code	Description
Intersects	`TFFFF`	“Two geometries intersect if they share any portion of space”
Overlaps	`TFFFF`	“Two geometries overlap if they share some but not all of the same space”
Equals	`TFFFF`	“Two geometries are topologically equal if their interiors intersect and no part of the interior or boundary of one geometry intersects the exterior of the other”
Disjoint	`FFFF****`	“Two geometries are disjoint: they have no point in common. They form a set of disconnected geometries.”
Touches	`FT*******`	`FT***`
Contains	`T***FF`	“A contains B: geometry B lies in A, and the interiors intersect”
Covers	`T****FF`	`T**FF`
Within	`T***FF`	`T*FF`
Covered by	`T***FF`	`T*FF`

Binary Predicates

Collectively, predicates define the type of relationship each 2D object has with another.
Of the ~ 512 unique relationships offered by the DE-9IM models a selection of ~ 10 have been named.
These are include in PostGIS/GEOS and are made accessible via R sf

Example

Geometry X is a 3 feature polygon colored in red
Geometry Y is a 4 feature polygon colored in blue

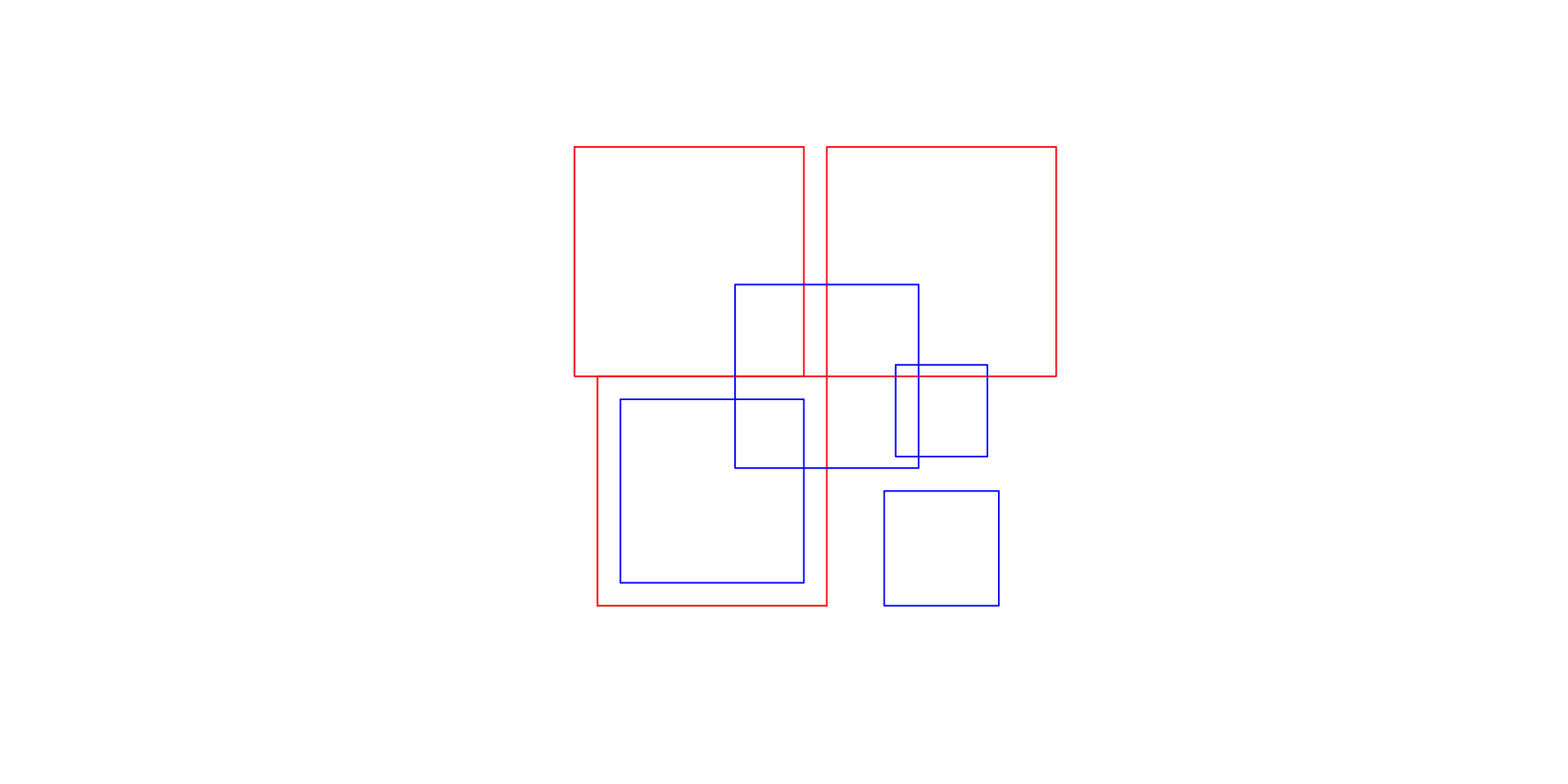
Named predicates in R

sf provides a set of functions that implement the DE-9IM model and named predicates. Each of these can return either a sparse or dense matrix.

sparse matrix

st_intersects(x,y)
#> Sparse geometry binary predicate list of length 3, where the predicate
#> was `intersects'
#>  1: 1, 3
#>  2: 2, 3
#>  3: 3

dense matrix

st_intersects(x, y, sparse = FALSE)
#>       [,1]  [,2] [,3]  [,4]
#> [1,]  TRUE FALSE TRUE FALSE
#> [2,] FALSE  TRUE TRUE FALSE
#> [3,] FALSE FALSE TRUE FALSE

st_disjoint(x, y, sparse = FALSE)
#>       [,1]  [,2]  [,3] [,4]
#> [1,] FALSE  TRUE FALSE TRUE
#> [2,]  TRUE FALSE FALSE TRUE
#> [3,]  TRUE  TRUE FALSE TRUE

st_touches(x, y, sparse = FALSE)
#>       [,1]  [,2]  [,3]  [,4]
#> [1,] FALSE FALSE FALSE FALSE
#> [2,] FALSE FALSE FALSE FALSE
#> [3,] FALSE FALSE FALSE FALSE

st_within(x, y, sparse = FALSE)
#>       [,1]  [,2]  [,3]  [,4]
#> [1,] FALSE FALSE FALSE FALSE
#> [2,] FALSE FALSE FALSE FALSE
#> [3,] FALSE FALSE FALSE FALSE

So…

binary predicates return conditional {T,F} relations based on predefined masks of the DE-9IM strings
Up to this point in class we have been using Boolean {T,F} masks to filter data.frames by columns:

fruits = c("apple", "orange", "lemon", "watermelon")

fruits == "apple"
#> [1]  TRUE FALSE FALSE FALSE

fruits %in% c("apple", "lemon")
#> [1]  TRUE FALSE  TRUE FALSE

Spatial Filtering

We can filter spatially, use st_filter as the function call
Here the boolean condition is not passed (e.g. name == WA)
But instead, is defined by a spatial predicate
The default is st_intersects but can be changed with the .predicate argument:

states = AOI::aoi_get(state = c("WA", "OR", "ID", "MT"))
wa <- filter(states, state_abbr == "WA") 

mutate(states,
       touch_s = st_touches(states, wa),
       touch_d = st_touches(states, wa, sparse = FALSE)) |> 
  select(state_name, contains('touch'))
#> Simple feature collection with 4 features and 3 fields
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -124.8485 ymin: 41.98818 xmax: -104.0397 ymax: 49.00244
#> Geodetic CRS:  WGS 84
#>   state_name touch_s touch_d                       geometry
#> 1 Washington           FALSE MULTIPOLYGON (((-121.5237 4...
#> 2     Oregon       1    TRUE MULTIPOLYGON (((-117.22 44....
#> 3      Idaho       1    TRUE MULTIPOLYGON (((-111.0455 4...
#> 4    Montana           FALSE MULTIPOLYGON (((-109.7985 4...

st_filter(states, wa, .predicate = st_touches) 
#> Simple feature collection with 2 features and 14 fields
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -124.7035 ymin: 41.98818 xmax: -111.0435 ymax: 49.00085
#> Geodetic CRS:  WGS 84
#>   state_region state_division feature_code state_name state_abbr   name
#> 1            4              9      1155107     Oregon         OR Oregon
#> 2            4              8      1779783      Idaho         ID  Idaho
#>   fip_class tiger_class combined_area_code metropolitan_area_code
#> 1      <NA>       G4000                 NA                   <NA>
#> 2      <NA>       G4000                 NA                   <NA>
#>   functional_status    land_area water_area fip_code
#> 1                 A 248628414476 6170965739       41
#> 2                 A 214049931578 2391569647       16
#>                         geometry
#> 1 MULTIPOLYGON (((-117.22 44....
#> 2 MULTIPOLYGON (((-111.0455 4...

Result

ggplot(states) + 
  geom_sf() + 
  geom_sf(data = wa, fill = "blue", alpha = .3) +
  geom_sf(data = st_filter(states, wa, .predicate = st_touches), fill = "red", alpha = .5) + 
  theme_void()

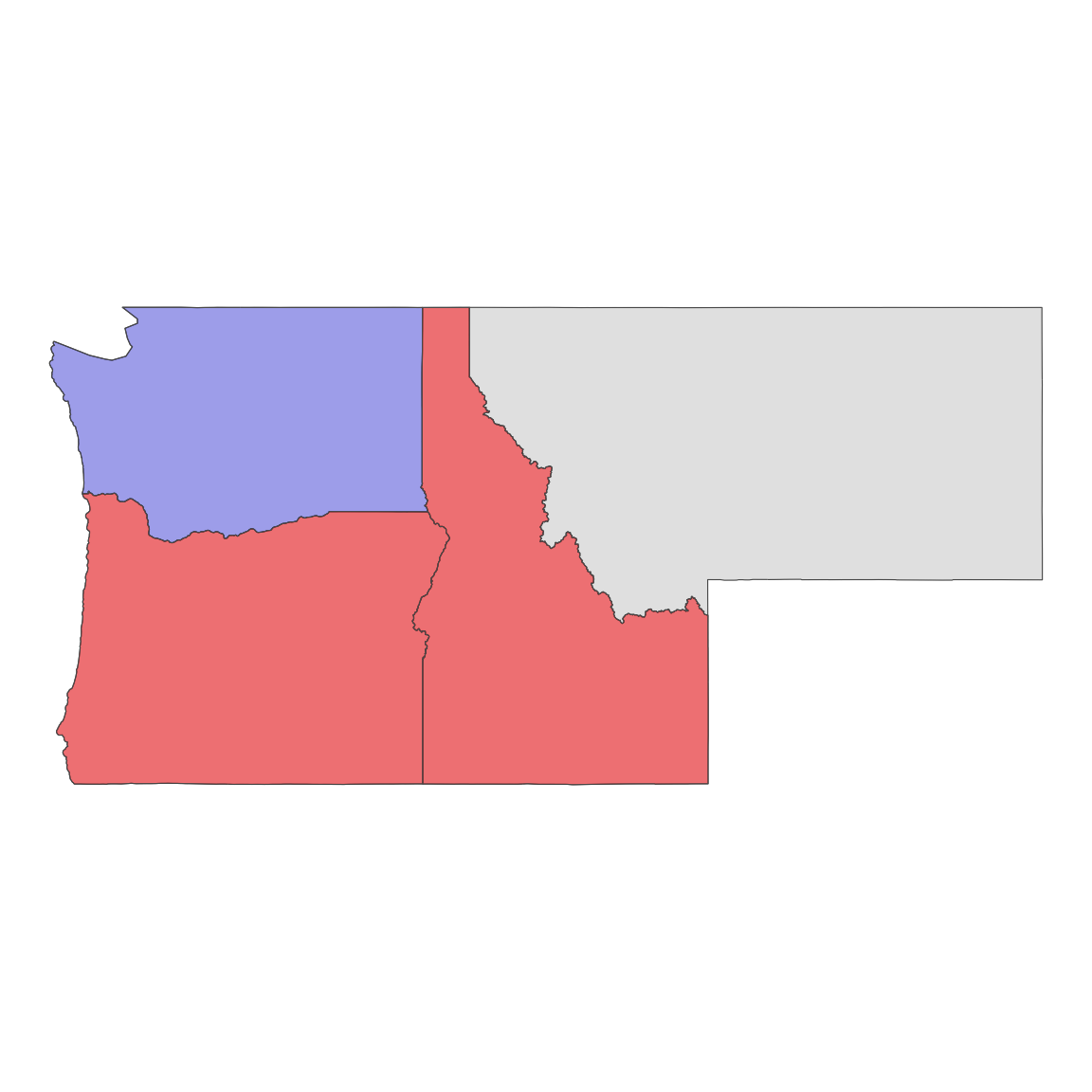
Spatial Joining

Joining two non-spatial datasets relies on a shared key that uniquely identifies each record in a table

Spatially joining data relies on shared geographic relations rather then a shared key
Like filter, these relations can be defined by a predicate
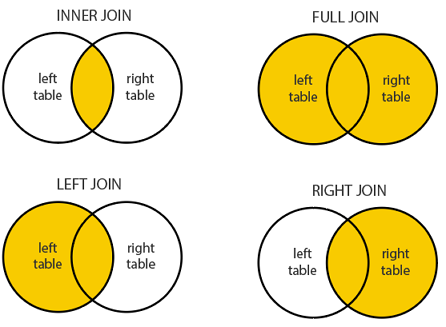
As with tabular data, mutating joins add data to the target object (x) from a source object (y).

st_join

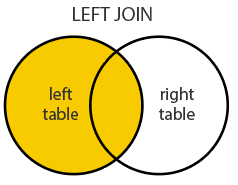
In sf st_join provides this joining capacity
By default, st_join performs a left join (Returns all records from x, and the matched records from y)

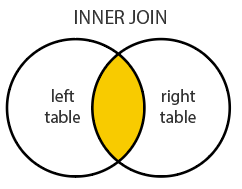
It can also do inner joins by setting left = FALSE.

The default predicate for st_join (and st_filter) is st_intersects
This can be changed with the join argument (see ?st_join for details).

Every Starbucks in the World

What county has the most Starbucks in each state?

(starbucks = readr::read_csv('../labs/data/directory.csv') |> 
  filter(!is.na(Latitude), Country == "US") |> 
  st_as_sf(coords = c("Longitude", "Latitude"), crs = 4326) |> 
  st_transform(5070))
#> Simple feature collection with 13608 features and 11 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -6223543 ymin: 278590.9 xmax: 2122577 ymax: 5307178
#> Projected CRS: NAD83 / Conus Albers
#> # A tibble: 13,608 × 12
#>    Brand     `Store Number` `Store Name` `Ownership Type` `Street Address` City 
#>  * <chr>     <chr>          <chr>        <chr>            <chr>            <chr>
#>  1 Starbucks 3513-125945    Safeway-Anc… Licensed         5600 Debarr Rd … Anch…
#>  2 Starbucks 74352-84449    Safeway-Anc… Licensed         1725 Abbott Rd   Anch…
#>  3 Starbucks 12449-152385   Safeway - A… Licensed         1501 Huffman Rd  Anch…
#>  4 Starbucks 24936-233524   100th & C S… Company Owned    320 W. 100th Av… Anch…
#>  5 Starbucks 8973-85630     Old Seward … Company Owned    1005 E Dimond B… Anch…
#>  6 Starbucks 72788-84447    Fred Meyer … Licensed         1000 E Northern… Anch…
#>  7 Starbucks 79549-106150   Safeway - A… Licensed         3101 PENLAND PK… Anch…
#>  8 Starbucks 75988-107245   ANC Main Te… Licensed         HMSHost, 500 We… Anch…
#>  9 Starbucks 11426-99254    Tudor Rd an… Company Owned    110 W. Tudor Rd… Anch…
#> 10 Starbucks 20349-108249   Fred Meyer-… Licensed         7701 Debarr Road Anch…
#> # ℹ 13,598 more rows
#> # ℹ 6 more variables: `State/Province` <chr>, Country <chr>, Postcode <chr>,
#> #   `Phone Number` <chr>, Timezone <chr>, geometry <POINT [m]>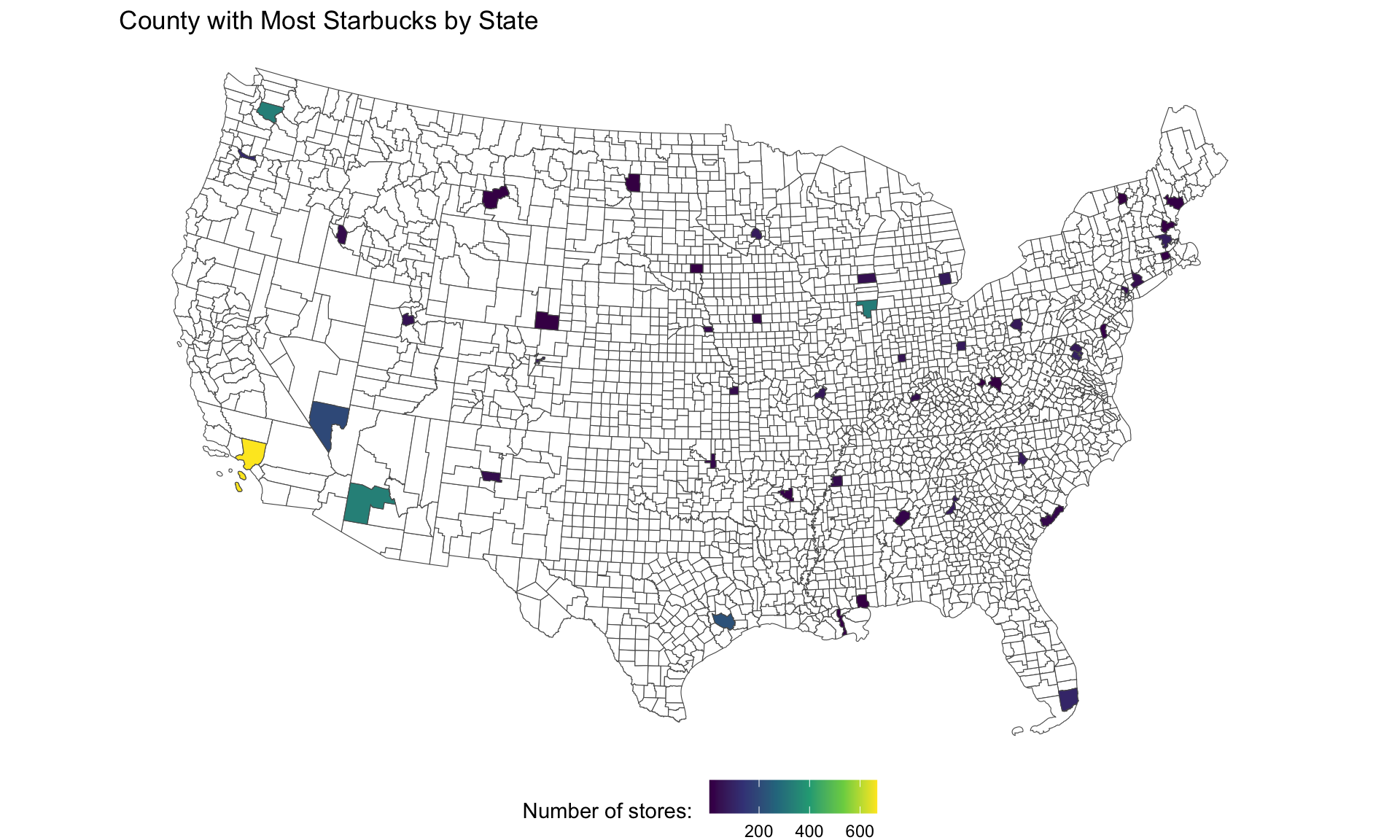

counties = aoi_get(state = "conus", county = "all") |> 
  st_transform(5070) |> 
  select(name, state_name)

topSB <- st_join(counties, starbucks) |> 
  group_by(name, state_name) |> 
  summarise(n = n()) |> 
  group_by(state_name) |> 
  slice_max(n, n = 1) |> 
  ungroup()

Neither joining nor filtering spatially alter the underlying geometry of the features
In cases where we seek to alter a geometry based on another, we need clipping methods

Clipping

Clipping is a form of subsetting that involves changing the geometry of at least some features.
Clipping can only apply to features more complex than points: (lines, polygons and their ‘multi’ equivalents).

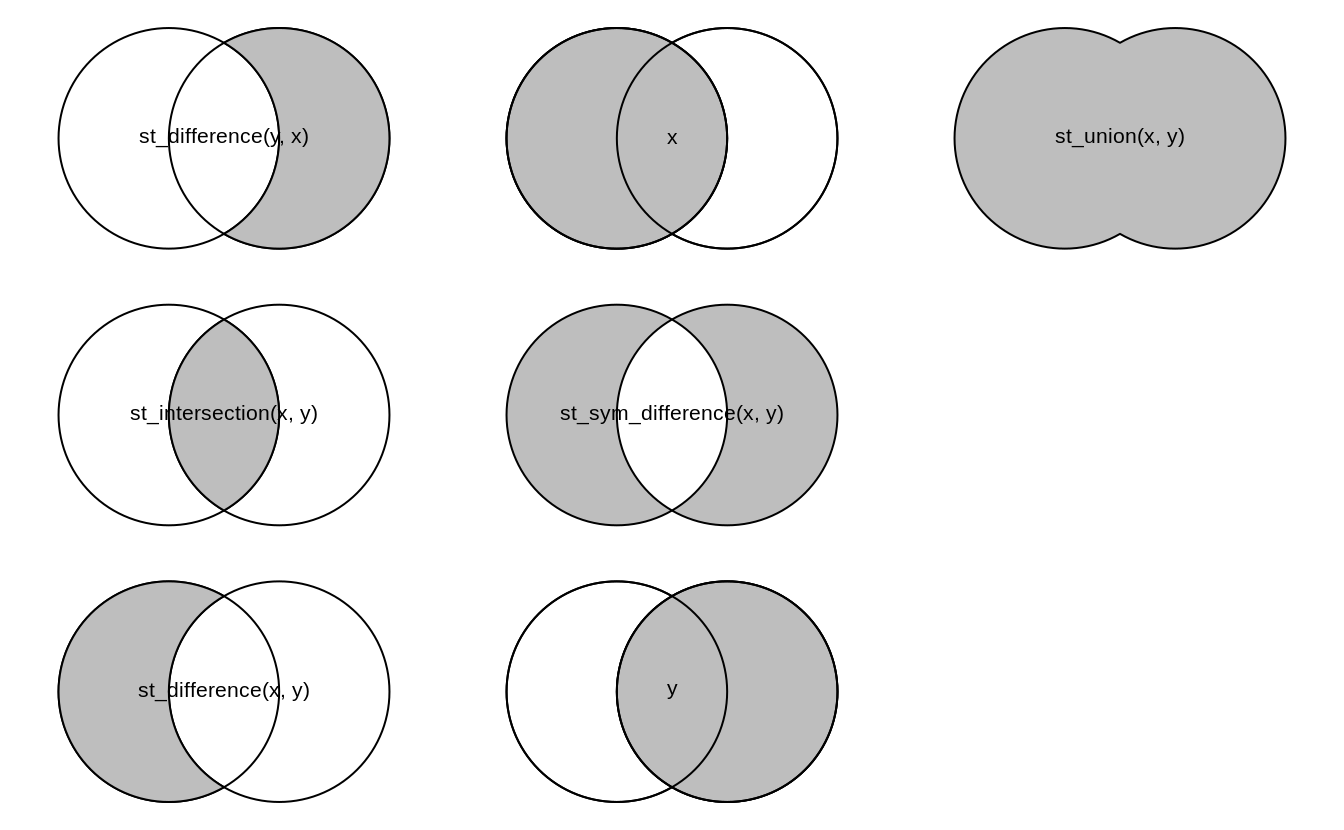
Clipping

wa = st_transform(wa, 5070)

st_intersection(wa, starbucks) |> 
  ggplot() + 
  geom_sf(data = wa, fill = "white") + 
  geom_sf(aes(color = name)) + 
  theme_void()

st_difference(starbucks, wa) |> 
  ggplot() + 
  geom_sf(data = wa, fill = "white") + 
  geom_sf(aes(color = name)) + 
  theme_void()

Spatial Subsetting

By default the data.frame subsetting methods we’ve seen (e.g [,]) implements st_intersection

wa = st_transform(wa, 5070)
wa_starbucks = starbucks[wa,] #<<

ggplot() + geom_sf(data = wa) + geom_sf(data = wa_starbucks) + theme_void()

Wrap up

Today we covered the following topics: - Spatial predicates and binary predicates - Spatial filtering and joining

Combined with your understanding of

Geometry and topology
Coordinate Reference Systems
Their integration with R

We are well suited to move on to raster data (gridded model) next time

Assignment

You have been tasked by the USACE of identify the urban population living along the Mississippi River system
You are interested in the county level since most flood control measures and flood response efforts are enforced by county EMAs
As such, you will need to identify the counties that intersect the Mississippi River system and then sum the population of the cities within those counties.
Your final results should be a map of the counties that intersect the Mississippi River system, colored by the total urban population in each county.

Assignment

To do this …

Navigate to here to download a shapefile fof the major world rivers
Unzip it and read in the shp file with read_sf
Filter it to include only the Mississippi River system
Use AOI::aoi_get() to get the county boundaries for all counties in CONUS.
Use st_filter to identify the counties that intersect the Mississippi River system
Make a map of the counties that intersect the Mississippi River system, along with the rivers themselves.
Read in the city data from last assignment/lab and ensure they are a sf object in the correct CRS
Use st_join to identify the cities that intersect the counties that intersect the Mississippi River system
Calculate the total urban population in each county by summing the population of the cities within each county that intesects the Mississippi River system.
Add this data to the subset of intersecting counties and use it to color you map using scale_*
Save your map as a png file in the images folder and submit it to Canvas.