(ny <- AOI::aoi_get(state = "NY") |>
st_transform(5070) |>
dplyr::select(name))
#> Simple feature collection with 1 feature and 1 field
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: 1319502 ymin: 2149150 xmax: 1997508 ymax: 2658543
#> Projected CRS: NAD83 / Conus Albers
#> name geometry
#> 1 New York MULTIPOLYGON (((1661335 263...Lecture 26
Introduction to Raster Data
Recap: sf and spatial concepts
Spatial phenomena can be thought of discrete objects with clear boundaries or as continuous phenomenon that can be observed everywhere, with no natural boundaries.
We have described these as objects and fields (Kuhn, 2012)
Objects are usually represented by vector data consisting of:
- a geometry (simple features (
sfc,sfg)) - some attribute information (
data.frame)
- a geometry (simple features (
In R these are unified as a
sfobjectField data is typically represented by raster data
For this, we will begin our discussions using the
terrapackage
terra
Like
sf,terrais an implementation of standard raster data modelThe model is used by all GIS platforms
Represented continuous data either as continuous or categorical values as a regular set of cells in a grid (matrix)
cells have: (1) resolution, (2) infered cell coordinate (centroid) (3) the coordinate and value apply to the entire cell area
Recap: R data structures
Vector:
- A vector can have dimensions
- A 1D vector in a collection of values
- A 2D vector is a matrix
- A 3D vector is an array
- A vector can have dimensions
List: a collection of objects
data.frame: a list with requirement of equal length column (vectors)
data.frames and lists (
sfc) defined our vector modelArrays will define our raster model
Spatial Extent
One last topic with respect to vector data (that will carry us into raster) is the idea of an extent:
In geometry, the minimum bounding box for a point set (stored as POINT, POLYLINE, POLYGON) in N dimensions is “…the box with the smallest measure within which all the points lie.”
We can extract bounding box coordinates with st_bbox
- returns: an object of class
bboxof length 4.
There is a method for creating an sfc form a bbox object
(bb = st_as_sfc(bb))
#> Geometry set for 1 feature
#> Geometry type: POLYGON
#> Dimension: XY
#> Bounding box: xmin: 1319502 ymin: 2149150 xmax: 1997508 ymax: 2658543
#> Projected CRS: NAD83 / Conus Albers
#> POLYGON ((1319502 2149150, 1997508 2149150, 199...
class(bb)
#> [1] "sfc_POLYGON" "sfc"
typeof(bb)
#> [1] "list"Result:
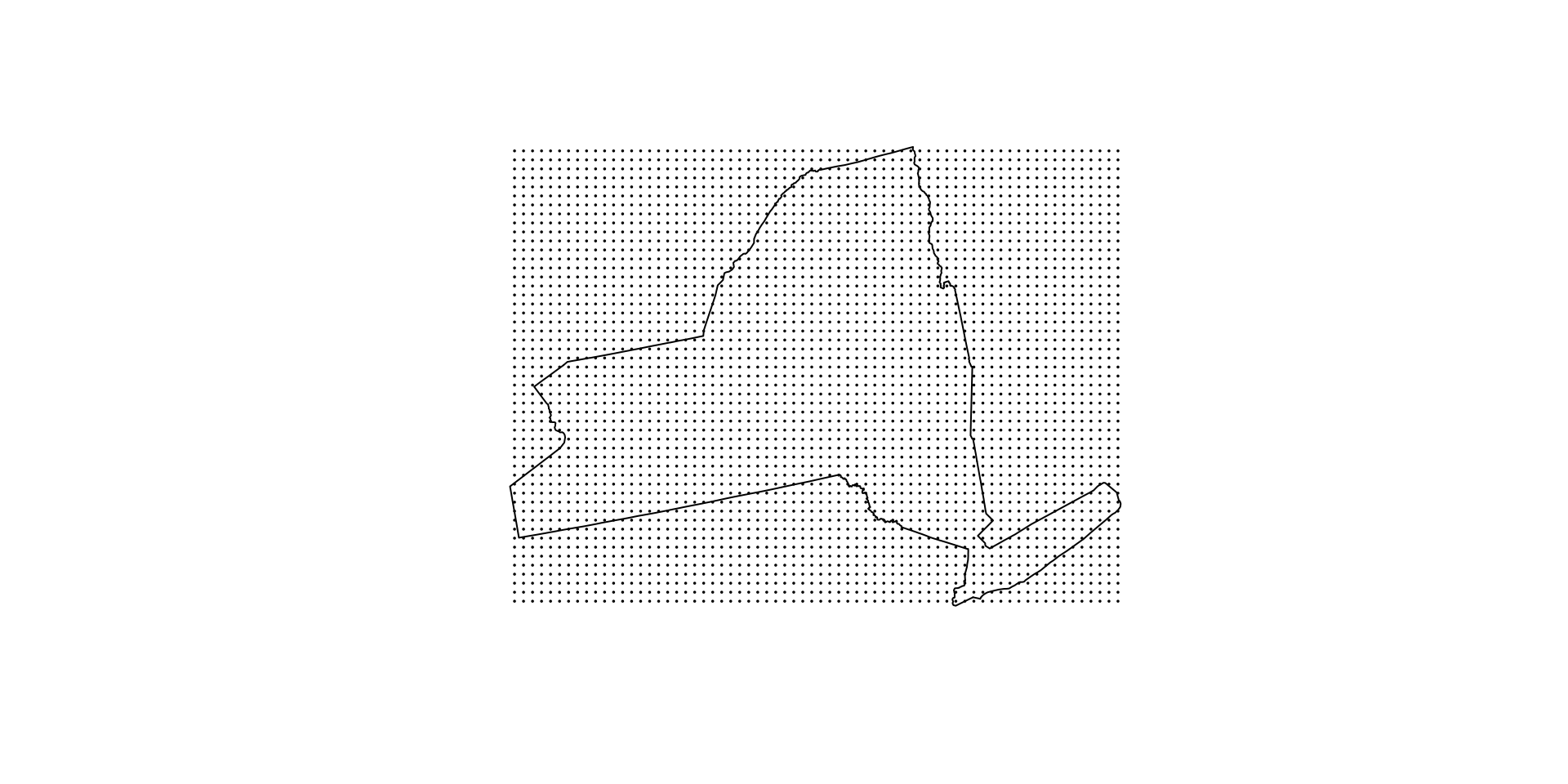
Extents can be discritized in a number of ways:
What makes up a regular tesselation
Alternative representation
Regular grids can also be indexed by their centroids
Raster Model
The raster model is one of the earliest and most widely used data models within geographic information systems (Tomlin, 1990; Goodchild, 1992, Maguire, 1992).
Typically used to record, analyze and visualize data with a continuous nature such as elevation, temperature (“GIS”), or reflected or emitted electromagnetic radiation (“Remote Sensing”)
Quotes are used because you’ll find from a data perspective these differences are artificial and a product of the ESRI/ENVI/ERDAS divide
The term
rasteroriginated from the German word for screen, implying a series of orthogonality oriented parallel lines.Digital raster objects most often take the form of a regularly spaced, grid-like pattern of rows and columns
Each element referred to as a cell, pixel, or grid point.
Many terms mean the same thing …
The entire raster is sometimes referred to as an “image”, “array”, “surface”, “matrix”, or “lattice” (Wise, 2000).
The all mean the same thing…
Cells of the raster are most often square, but may be rectangular (with differing resolutions in x and y directions) or other shapes that can be tessellated such as triangles and hexagons (Figure below from Peuquet, 1984).

Photos and Computers …


Aerial Imagery (really just a photo 😄)

What is stored in these cells?
Categorical Values (integer/factor)
Continuous Values (numeric)
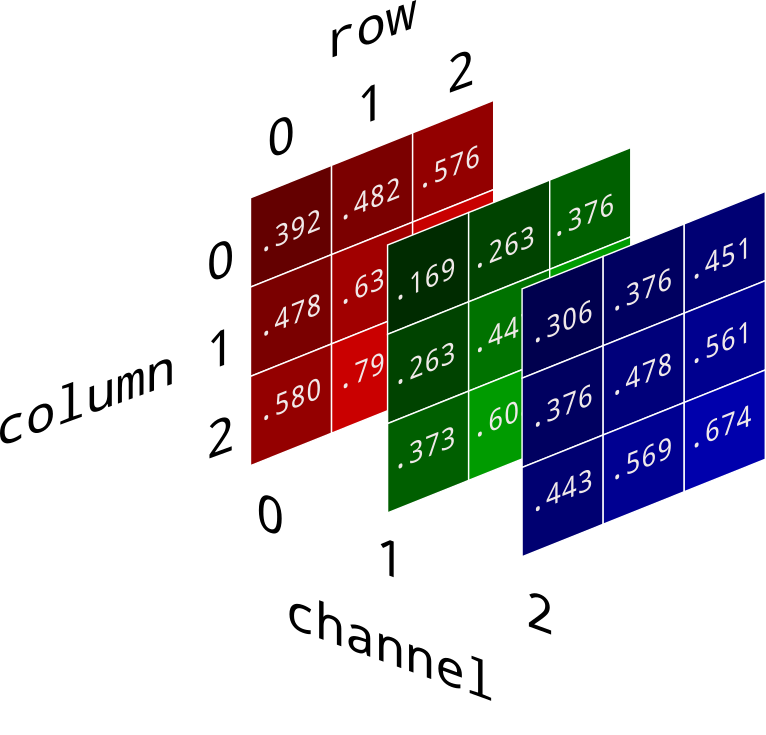
Spectral Values
- Either Color, or sensor
Why do we care?
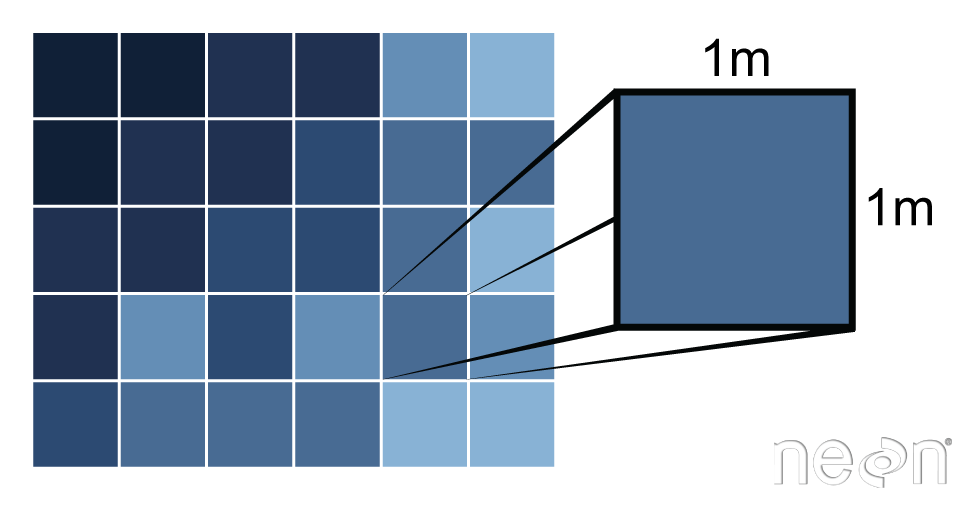
Pixels are the base unit of raster data and have a resolution
This is the X and the Y dimension of each cell in the units of the CRS
Raster images seek to discritize the real world into cell-based values
- Again either integer (categorical), continuous, or signal
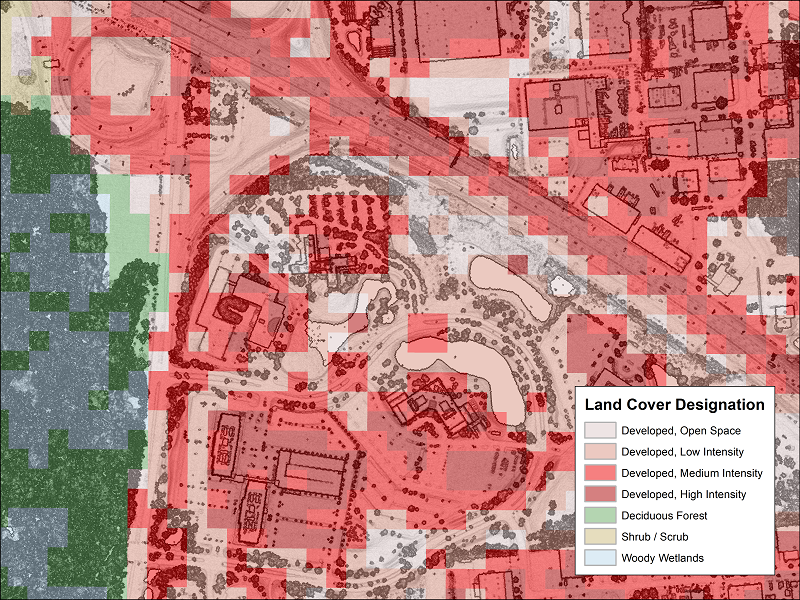
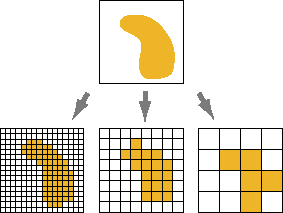
Resolution drives image clarity (granulairty)
- Higher resolution (smaller cells) = more detail, but bigger data!

All rasters have an extent!
This is the same extent as a bounding box
Can be described as 4 values (xmin,ymin,xmax,ymax)

Implicit Coordinates
Unlike vector data, the raster data model stores the coordinate of the grid cells indirectly
Coordinates are derived from the reference (Xmin,Ymin) the resolution, and the cell index (e.g. [100,150])
For example: If we want the coordinates of a value in the 3rd row and the 40th column of a raster matrix, we have to move from the origin (Xmin, Ymin) (3 x Xres) in x-direction and (40 x Yres) in y-direction

So, any image (.png, .tif, .gif) can be read as a raster…
The raster is defined by the extent and resolution of the cells
To be spatial, the extent (thus coordinates) must be grounded in an CRS
(img = terra::rast('images/17-raster-extent.png'))
#> class : SpatRaster
#> dimensions : 788, 1067, 4 (nrow, ncol, nlyr)
#> resolution : 1, 1 (x, y)
#> extent : 0, 1067, 0, 788 (xmin, xmax, ymin, ymax)
#> coord. ref. :
#> source : 17-raster-extent.png
#> names : 17-rast~xtent_1, 17-rast~xtent_2, 17-rast~xtent_3, 17-rast~xtent_4terra I/O
- terra is an R pacakge that binds to GDAL exposing the drivers for I/0
Local Raster Data
- All raster data is read with
rast() - Critically,
rast()reads the data header, before calling data into memory - Only when an operation that needs the values is called, is the data streamed into memory
rast("data/foco-elev.tif")
#> class : SpatRaster
#> dimensions : 725, 572, 1 (nrow, ncol, nlyr)
#> resolution : 30, 30 (x, y)
#> extent : -769695, -752535, 1978485, 2000235 (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs
#> source : foco-elev.tif
#> name : dem
#> min value : 146730
#> max value : 197781Raster Data from the Web
GDAL exposes a number of Virtual System Interfaces (VSI) that allow for reading across various data protocols! These are implemented by prefixing a URL with the needed interface
- http(s):
/vsicurl/ - s3:
/vsis3/ - zip directories:
/vsizip/,/vsitar/ - and more!
url <- 'https://raw.githubusercontent.com/mikejohnson51/csu-ess-330/a993e03df117a76c609ff4c018055f8c821a6de9/resources/foco-elev.tif'
rast(glue::glue("/vsicurl/{url}"))
#> class : SpatRaster
#> dimensions : 750, 591, 1 (nrow, ncol, nlyr)
#> resolution : 29.01279, 29.01279 (x, y)
#> extent : -769693.5, -752546.9, 1978477, 2000236 (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs
#> source : foco-elev.tif
#> name : foco-elev
#> min value : 1466
#> max value : 1975CONUS DEM
- The CONUS DEM is a 1 arc-second (30m) resolution elevation data set for the continental United States stored in an an s3 bucket (Amazon Cloud)
- The s3 vsi function allows us to read the data directly from the cloud
- The data is stored in a virtual raster format (VRT) which is a pointer to many data files…
rast('/vsis3/lynker-spatial/gridded-resources/dem.vrt')
#> class : SpatRaster
#> dimensions : 114503, 163008, 1 (nrow, ncol, nlyr)
#> resolution : 30, 30 (x, y)
#> extent : -2470965, 2419275, 186285, 3621375 (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs
#> source : dem.vrt
#> name : demRaster Data in R
A SpatRast represents single-layer (variable) raster data.
A SpatRast always stores the fundamental parameters that describe it. - The number of columns and rows, - The spatial extent - The Coordinate Reference System.
In addition, a SpatRast can store information about the file where raster values are stored (if there is such a file).
Here we construct an empty raster:
Extract Diminisionality …
Raster Values
values can be extracted with values()
Assigning a values as a vector
values(r) <- 1:ncell(r)
r
#> class : SpatRaster
#> dimensions : 20, 20, 1 (nrow, ncol, nlyr)
#> resolution : 2, 2 (x, y)
#> extent : -120, -80, 20, 60 (xmin, xmax, ymin, ymax)
#> coord. ref. : lon/lat WGS 84 (CRS84) (OGC:CRS84)
#> source(s) : memory
#> name : lyr.1
#> min value : 1
#> max value : 400
head(values(r))
#> lyr.1
#> [1,] 1
#> [2,] 2
#> [3,] 3
#> [4,] 4
#> [5,] 5
#> [6,] 6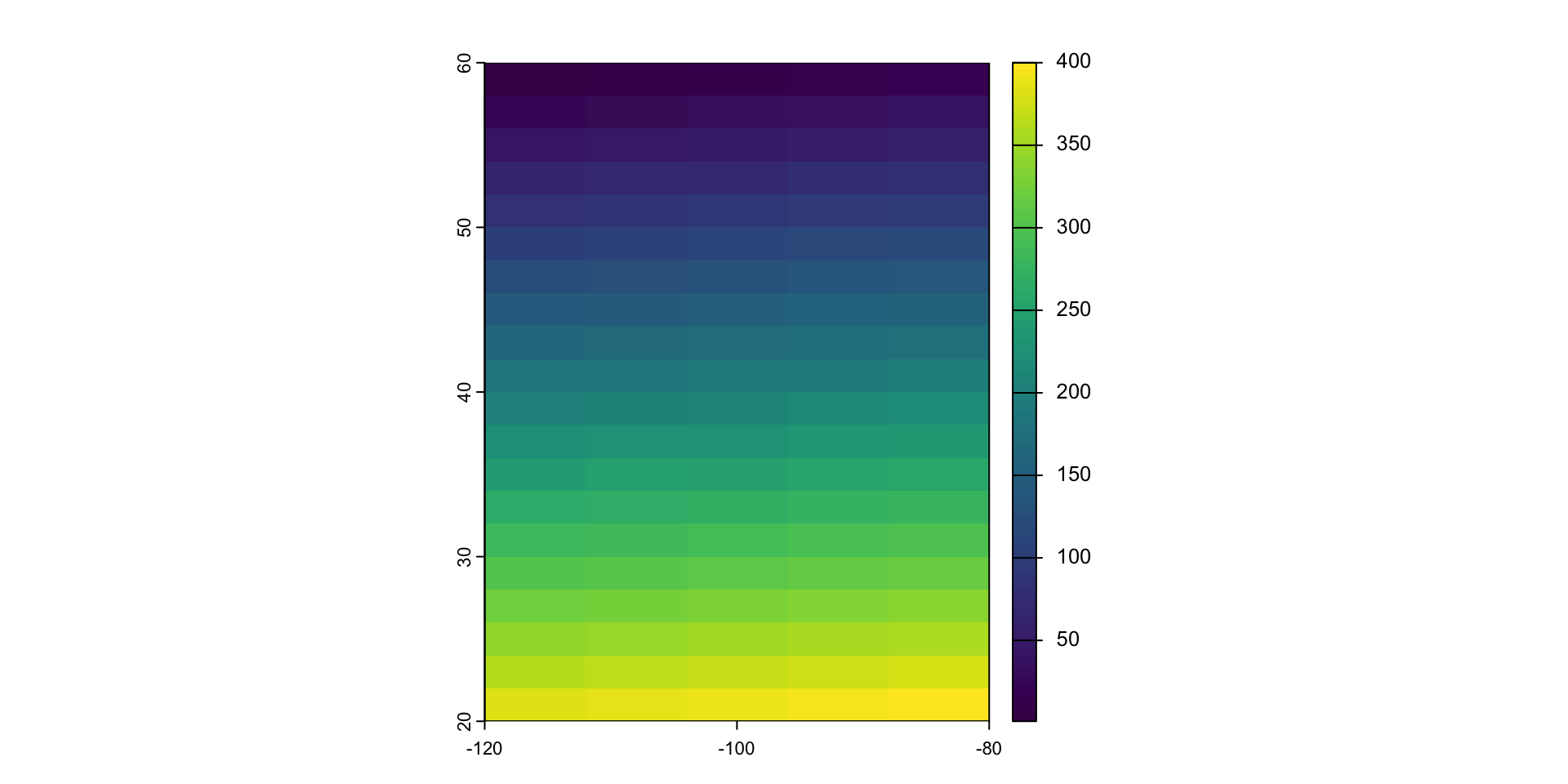
Raster is S4
Compared to S3, the S4 object system is much stricter, and much closer to other Object Oriented systems.
What does this mean for us?
Data is structured with a “representation”
which is a list of slot (or attributes), giving their names and classes, accessed with @
str(r, max.level = 2)
#> S4 class 'SpatRaster' [package "terra"]
r@pntr
#> C++ object <0x128469540> of class 'SpatRaster' <0x10ee8ad30>
r@pntr$ncol
#> Class method definition for method ncol()
#> function ()
#> {
#> " unsigned long ncol() \n docstring : ncol"
#> .External(list(name = "CppMethod__invoke_notvoid", address = <pointer: 0x10e8211a0>,
#> dll = list(name = "Rcpp", path = "/Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library/Rcpp/libs/Rcpp.so",
#> dynamicLookup = TRUE, handle = <pointer: 0x79b993b0>,
#> info = <pointer: 0x10e8be530>, forceSymbols = FALSE),
#> numParameters = -1L), <pointer: 0x10ee8ad30>, <pointer: 0x10ee8edd0>,
#> .pointer)
#> }
#> <environment: 0x12cdc9b90>Access via Function
ext(r)
#> SpatExtent : -120, -80, 20, 60 (xmin, xmax, ymin, ymax)
crs(r)
#> [1] "GEOGCRS[\"WGS 84 (CRS84)\",\n DATUM[\"World Geodetic System 1984\",\n ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n LENGTHUNIT[\"metre\",1]]],\n PRIMEM[\"Greenwich\",0,\n ANGLEUNIT[\"degree\",0.0174532925199433]],\n CS[ellipsoidal,2],\n AXIS[\"geodetic longitude (Lon)\",east,\n ORDER[1],\n ANGLEUNIT[\"degree\",0.0174532925199433]],\n AXIS[\"geodetic latitude (Lat)\",north,\n ORDER[2],\n ANGLEUNIT[\"degree\",0.0174532925199433]],\n USAGE[\n SCOPE[\"unknown\"],\n AREA[\"World\"],\n BBOX[-90,-180,90,180]],\n ID[\"OGC\",\"CRS84\"]]"
nrow(r)
#> [1] 20
ncol(r)
#> [1] 20
head(values(r))
#> lyr.1
#> [1,] 1
#> [2,] 2
#> [3,] 3
#> [4,] 4
#> [5,] 5
#> [6,] 6Assignment
- Starting with this base …
… construct a VSI prefixed URL that allows rast to read the data directly from our class Github Repo.
Once the date is read in, describe the structure of the data in a few sentences.
Nativly, the data has a horizonal unit of
cm. Multiply the data by0.0328084to convert the data to feet.Extract the values from the raster into a data.frame by using the
dataframe=TRUEparameter in thevalues()function.Use
ggpubrto create a density plot of the elevation data in feet. Equit the plot with clear labs, and a title as well as a theme.Save your plot as a
pngfile with ggsave and submit to the Canvase Dropbox.