Lecture 27

Raster Modification

Core Raster Principles

1. Extent

When dealing with raster data, the extent is a fondational component of the raster data structure
- That is, we need to know the area the raster is covering!

Image Source: National Ecological Observatory Network (NEON)

2. Discretization

Once we know the extent, we need to know how that space is split up

Two complimentary bit of information can tell us this:

Resolution (res)
Number of row and number of columns (nrow/ncol)

Image Source: National Ecological Observatory Network (NEON)

3. CRS

The Coordinate Reference System (CRS) is a system that uses coordinate values to represent the location of points in space
The CRS is a critical component of the raster data structure

Values

The values of the raster are the data that is stored in the raster cells
They are represented by an vector of data that can be unfolded according to the row/column/layer structure in the header - just like how R can fold an array into a matrix or array

So,

A raster is made of an extent, and a resolution / row-column structure

A vector of values fill that structure (same way a vector in R can have diminisons)
- These values are often scaled to integers to reduce file size
Values are referenced in cartisian space, based on cell index
A CRS along with the extent, can provide spatial reference / coordinates

General Process

Almost all remote sensing / image analysis begins with the same basic steps:

Identifying an area of interest (AOI)
Identifying and downloading the relevant images or products
Analyzing the raster products

The definition of a AOI is critical because raster data in continuous, therefore we need to define the bounds of the study rather then the bounds of the objects

But, objects often (even typically) define our bounds

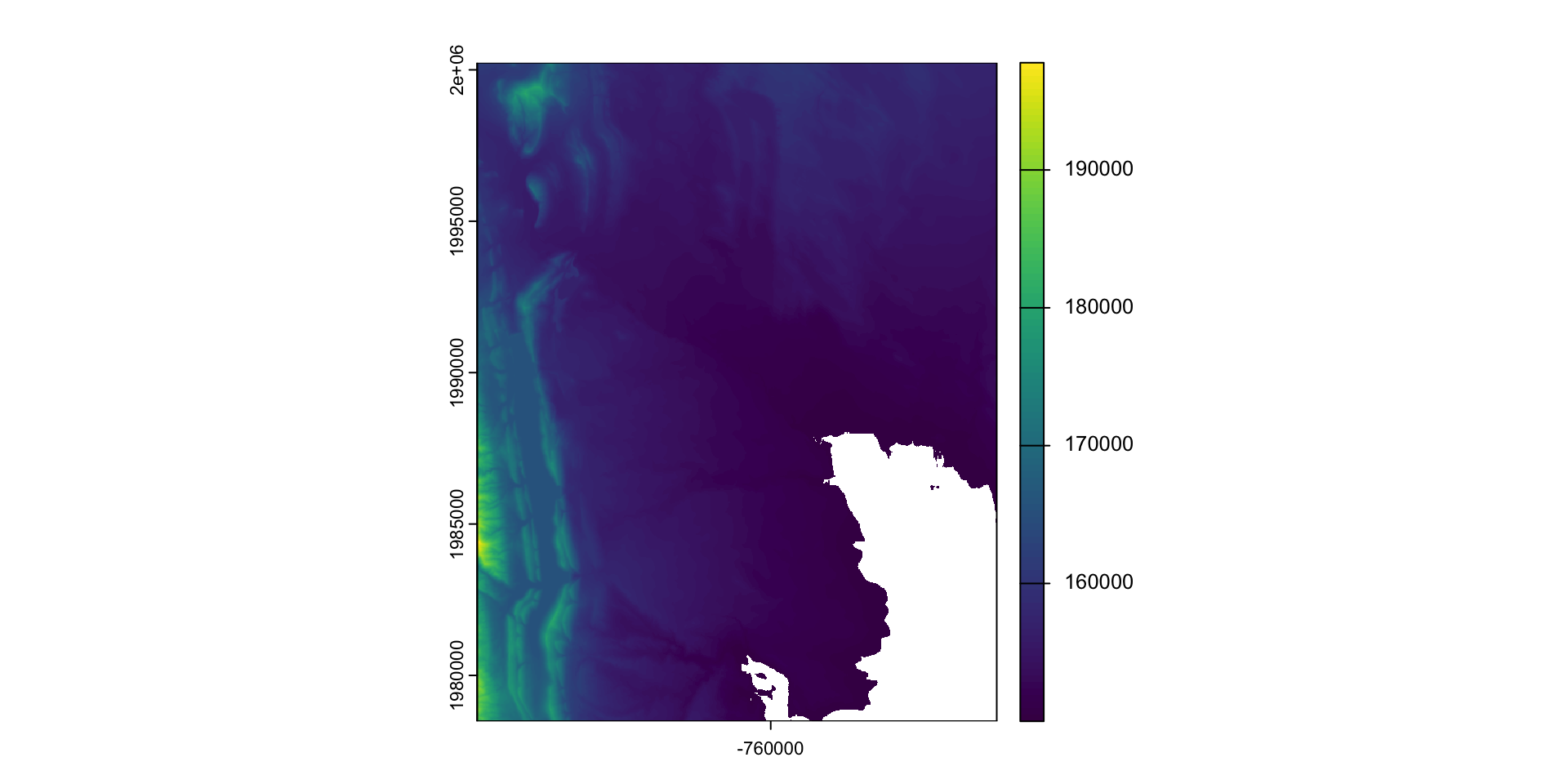
Find elevation data for Fort Collins:

Define the AOI

(bb = AOI::geocode("Fort Collins", bbox = TRUE) |> 
  st_transform(5070))

Read data from elevation map tiles, for a specific zoom, and crop to the AOI

elev = rast('/vsis3/lynker-spatial/gridded-resources/dem.vrt') |> 
  crop(bb)

writeRaster(elev, filename = "data/foco-elev.tif", overwrite = TRUE)

writeRaster(elev, filename = "../resources/foco-elev-cm.tif", overwrite = TRUE)

The resulting raster …

(elev = rast("data/foco-elev.tif"))
#> class       : SpatRaster 
#> dimensions  : 725, 572, 1  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : -769695, -752535, 1978485, 2000235  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs 
#> source      : foco-elev.tif 
#> name        :    dem 
#> min value   : 146730 
#> max value   : 197781

Raster Values

v <- values(elev)
class(v)
#> [1] "matrix" "array"
dim(v)
#> [1] 414700      1
length(v)
#> [1] 414700

elev
#> class       : SpatRaster 
#> dimensions  : 725, 572, 1  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : -769695, -752535, 1978485, 2000235  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs 
#> source      : foco-elev.tif 
#> name        :    dem 
#> min value   : 146730 
#> max value   : 197781

Raster Values

# The length of the vector is equal to the rows * columns
length(v) == nrow(elev) * ncol(elev)
#> [1] TRUE
# The span of the x extent divided by the resolution equals the raster rows
((xmax(elev) - xmin(elev)) / res(elev)[1]) == ncol(elev) 
#> [1] TRUE
# The span of the x extent divided by the number of rows equals the raster resolution
((xmax(elev) - xmin(elev)) / ncol(elev)) == res(elev)[1] 
#> [1] TRUE

All image files are the same!

download.file(url = "https://a.tile.openstreetmap.org/18/43803/104352.png",
              destfile = "data/104352.png")
img = png::readPNG("data/104352.png")
class(img)
#> [1] "array"
typeof(img)
#> [1] "double"
dim(img)
#> [1] 256 256   3

img[1,1,1:3]
#> [1] 1.0000000 1.0000000 0.9333333
rgb(1.0000000, 0.9607843, 0.8980392)
#> [1] "#FFF5E5"

Google Color Picker

Raster Algebra

So our raster data is stored as a large numeric array/vector
Many generic functions allow for simple algebra on Raster objects,
These include:
- normal algebraic operators such as +, -, *, /
- logical operators such as >, >=, <,==, !
- functions like abs, round, ceiling, floor, trunc, sqrt, log, log10, exp, cos, sin, atan, tan, max, min, range, prod, sum, any, all

Raster Algebra

In these functions you can mix SpatRast objects with numbers, as long as the first argument is a raster object.
That means you can add 100 to a raster object but not a raster object to 100

# GOOD
raster + 100

# BAD
100 + raster

For example:

elev + 100
#> class       : SpatRaster 
#> dimensions  : 725, 572, 1  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : -769695, -752535, 1978485, 2000235  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs 
#> source(s)   : memory
#> varname     : foco-elev 
#> name        :    dem 
#> min value   : 146830 
#> max value   : 197881
log10(elev)
#> class       : SpatRaster 
#> dimensions  : 725, 572, 1  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : -769695, -752535, 1978485, 2000235  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs 
#> source(s)   : memory
#> varname     : foco-elev 
#> name        :      dem 
#> min value   : 5.166519 
#> max value   : 5.296185

Replacement

Raster values can be replaced on a conditional statements
Doing this changes the underlying data!
If you want to retain the original data, you must make a copy of the base layer

plot(elev)

elev2 = elev #<<
elev2[elev2 <= 150000] = NA #<<
plot(elev2)

Modifying a raster

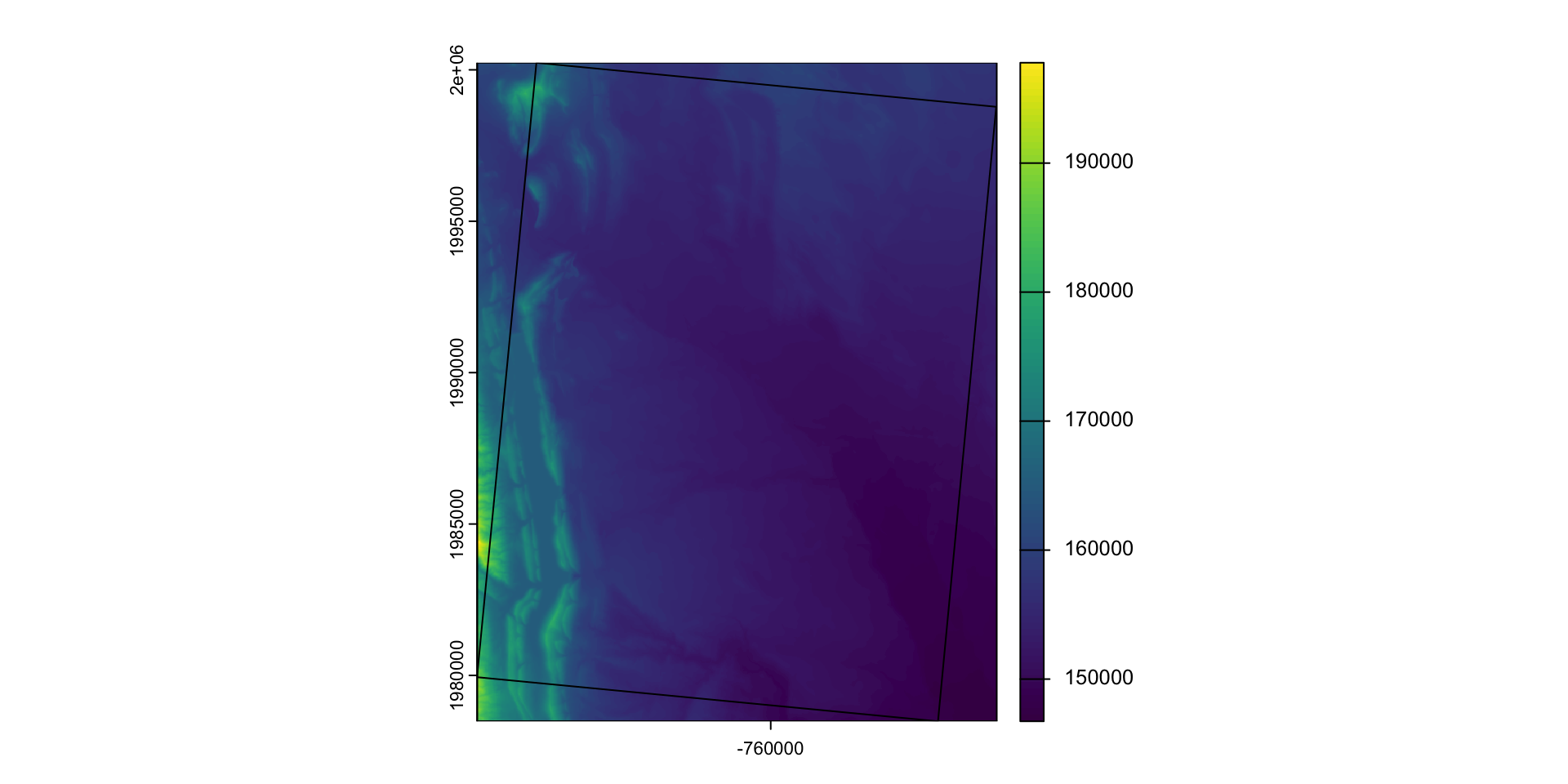
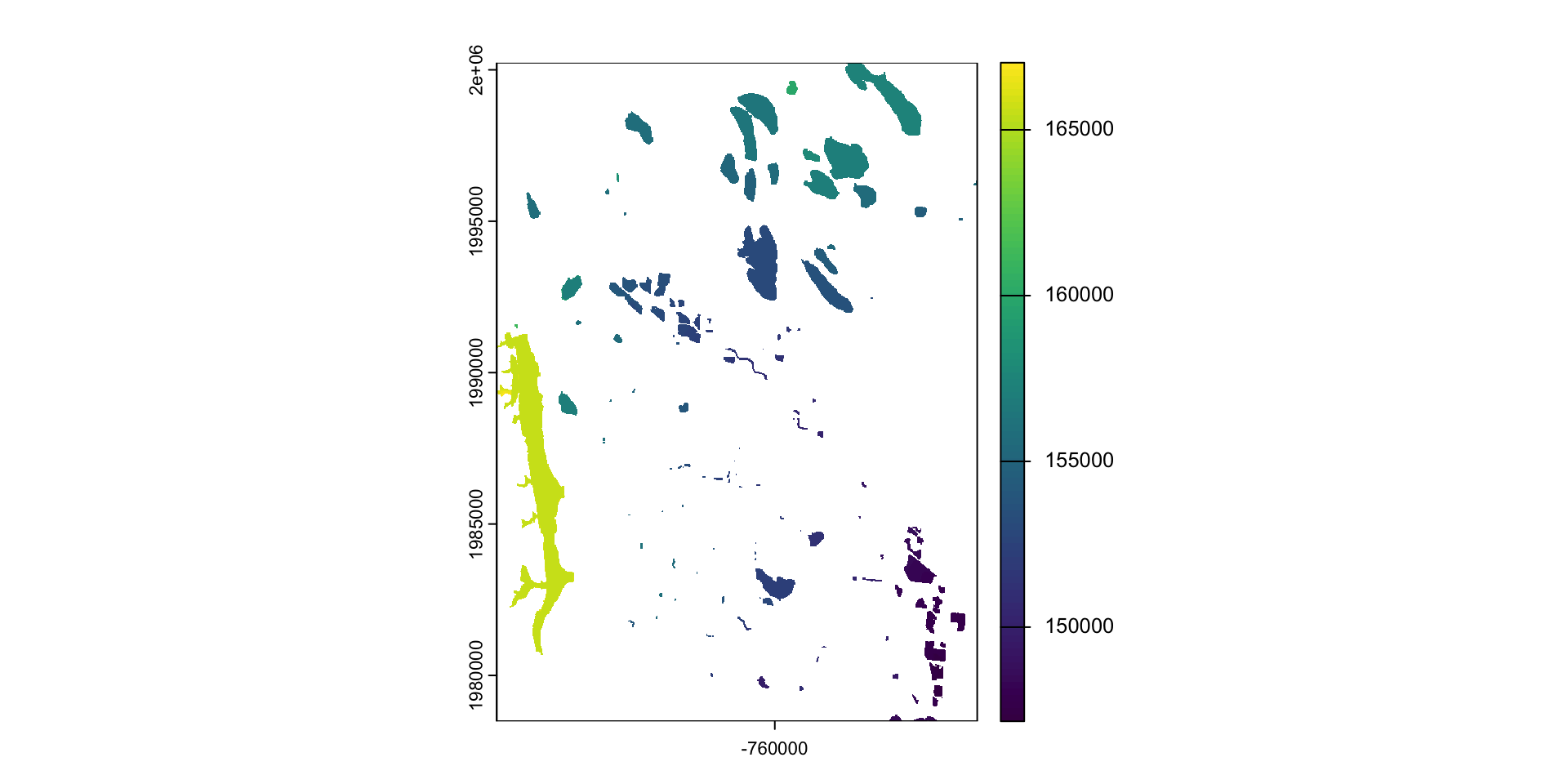
When we want to modify the extent of a raster we can clip it to a new bounds

crop: lets you reduce the extent of a raster to the extent of another, overlapping object:

# remotes::install_github("mikejohnson51/AOI")
fc = AOI::geocode("Fort Collins", bbox = TRUE) |> 
  st_transform(crs(elev))

plot(elev)
plot(fc, add = TRUE, col = NA)

fc_elev = crop(elev, fc) #<<
plot(fc_elev)

Modifying the underlying data:

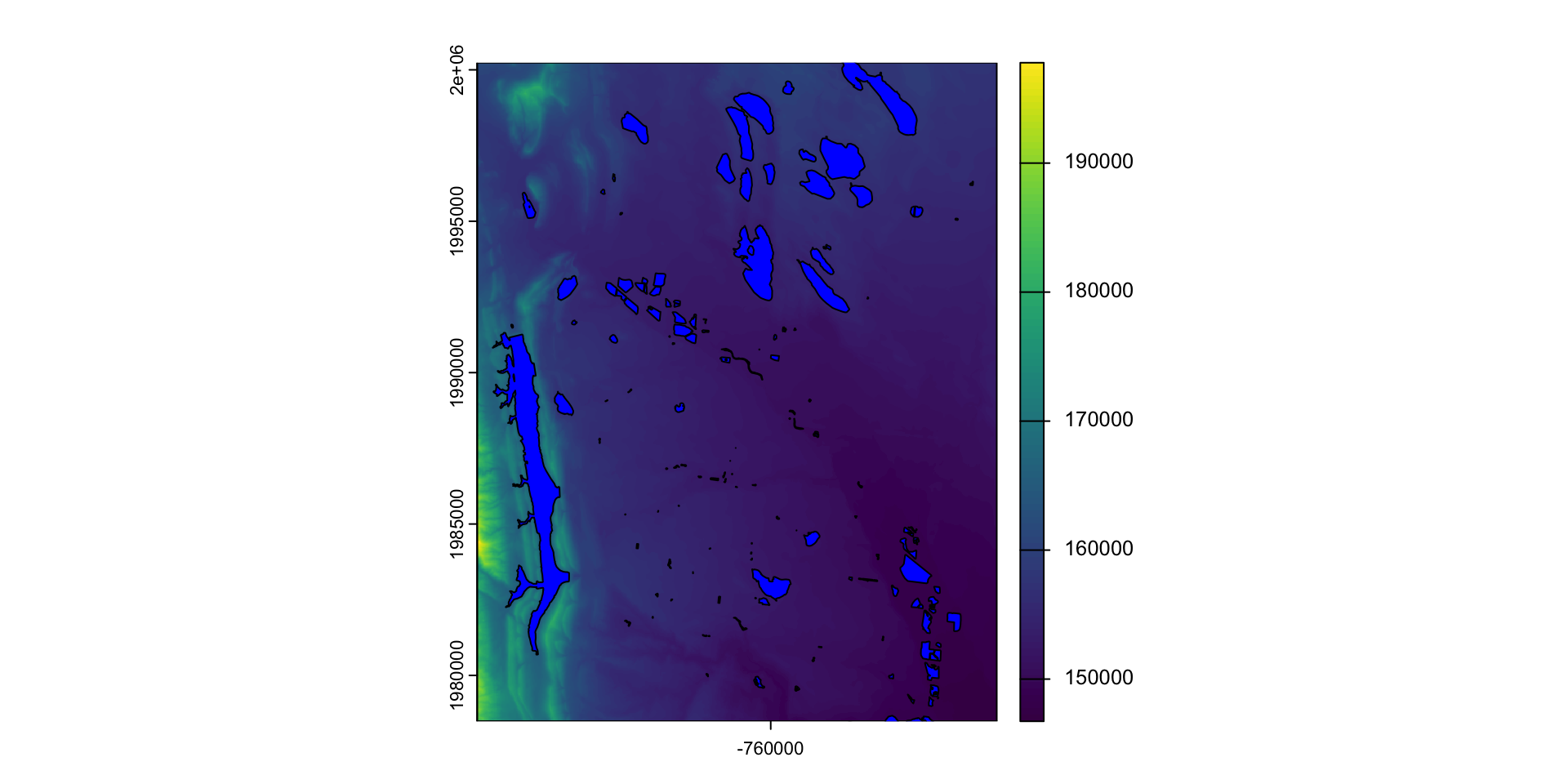
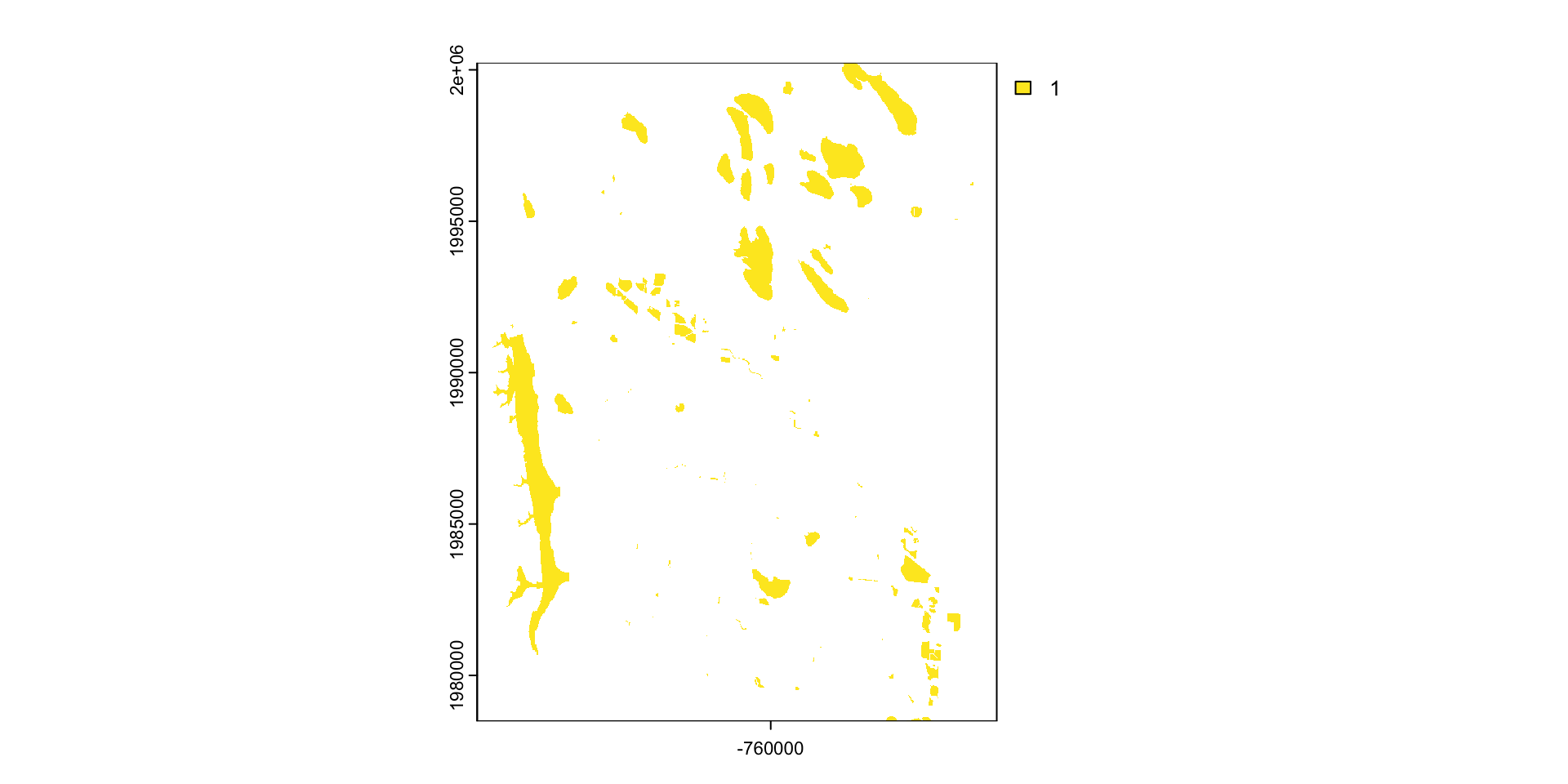
mask: mask takes an input object (sf or SpatRast) and set anything not undelying the input to a new value (default = NA)

library(osmdata)
#> Data (c) OpenStreetMap contributors, ODbL 1.0. https://www.openstreetmap.org/copyright

osm = osmdata::opq(st_bbox(st_transform(fc,4326))) |> 
  add_osm_feature("water") |> 
  osmdata_sf()

(poly = osm$osm_polygons |> 
  st_transform(crs(elev)))
#> Simple feature collection with 181 features and 17 fields
#> Geometry type: POLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -769181 ymin: 1977155 xmax: -753314.8 ymax: 2000444
#> Projected CRS: unnamed
#> First 10 features:
#>            osm_id              name         alt_name area basin boat
#> 6051656   6051656              <NA>             <NA> <NA>  <NA> <NA>
#> 23598705 23598705          Lee Lake             <NA> <NA>  <NA> <NA>
#> 23598868 23598868              <NA>             <NA> <NA>  <NA> <NA>
#> 23598945 23598945      College Lake             <NA> <NA>  <NA> <NA>
#> 23599224 23599224       Warren Lake             <NA> <NA>  <NA> <NA>
#> 23599227 23599227 Harmony Reservoir             <NA> <NA>  <NA> <NA>
#> 23599320 23599320              <NA>             <NA> <NA>  <NA> <NA>
#> 23599327 23599327              <NA>             <NA> <NA>  <NA> <NA>
#> 44074911 44074911     Lake Sherwood Nelson Reservoir <NA>  <NA> <NA>
#> 47471957 47471957              <NA>             <NA> <NA>  <NA> <NA>
#>          description  ele gnis:feature_id intermittent landuse layer natural
#> 6051656         <NA> <NA>            <NA>         <NA>    <NA>  <NA>    <NA>
#> 23598705        <NA> <NA>            <NA>         <NA>    <NA>  <NA>   water
#> 23598868        <NA> <NA>            <NA>         <NA>    <NA>  <NA>    <NA>
#> 23598945        <NA> <NA>            <NA>         <NA>    <NA>  <NA>   water
#> 23599224        <NA> <NA>            <NA>         <NA>    <NA>  <NA>   water
#> 23599227        <NA> <NA>            <NA>         <NA>    <NA>  <NA>   water
#> 23599320        <NA> <NA>            <NA>         <NA>    <NA>  <NA>   water
#> 23599327        <NA> <NA>            <NA>         <NA>    <NA>  <NA>   water
#> 44074911        <NA> 1512          201223         <NA>    <NA>  <NA>   water
#> 47471957        <NA> <NA>            <NA>         <NA>    <NA>  <NA>   water
#>          place salt source     water                       geometry
#> 6051656   <NA> <NA>   <NA>      <NA> POLYGON ((-762901.7 1988981...
#> 23598705  <NA> <NA>   <NA>      lake POLYGON ((-765209.9 1991246...
#> 23598868  <NA> <NA>   <NA>      <NA> POLYGON ((-767955.5 1985345...
#> 23598945  <NA> <NA>   <NA>      lake POLYGON ((-766871.6 1989267...
#> 23599224  <NA> <NA>   <NA> reservoir POLYGON ((-760465.5 1983486...
#> 23599227  <NA> <NA>   <NA> reservoir POLYGON ((-760046.6 1982348...
#> 23599320  <NA> <NA>   <NA>      pond POLYGON ((-762458.2 1991222...
#> 23599327  <NA> <NA>   <NA>      pond POLYGON ((-763462.8 1992438...
#> 44074911  <NA> <NA>   <NA> reservoir POLYGON ((-758628.3 1984729...
#> 47471957  <NA> <NA>   <NA> reservoir POLYGON ((-764440.4 1992962...

plot(fc_elev)
plot(poly, col = "blue", add  = TRUE)

ma =  mask(fc_elev, poly)
ma2 = mask(fc_elev, poly, inverse = TRUE)
plot(c(fc_elev, ma, ma2))

What is `mask` doing?

NA * 7
#> [1] NA

mask_r = rasterize(poly, fc_elev, background = NA)
plot(mask_r)

base_mask = mask_r * fc_elev
plot(base_mask)

Crop or/and mask

Crop is more efficient then mask
Often you will want to mask and crop a raster
The correct way to do this is crop then mask

cm = crop(fc_elev, poly) |>  
  mask(poly)

plot(cm)

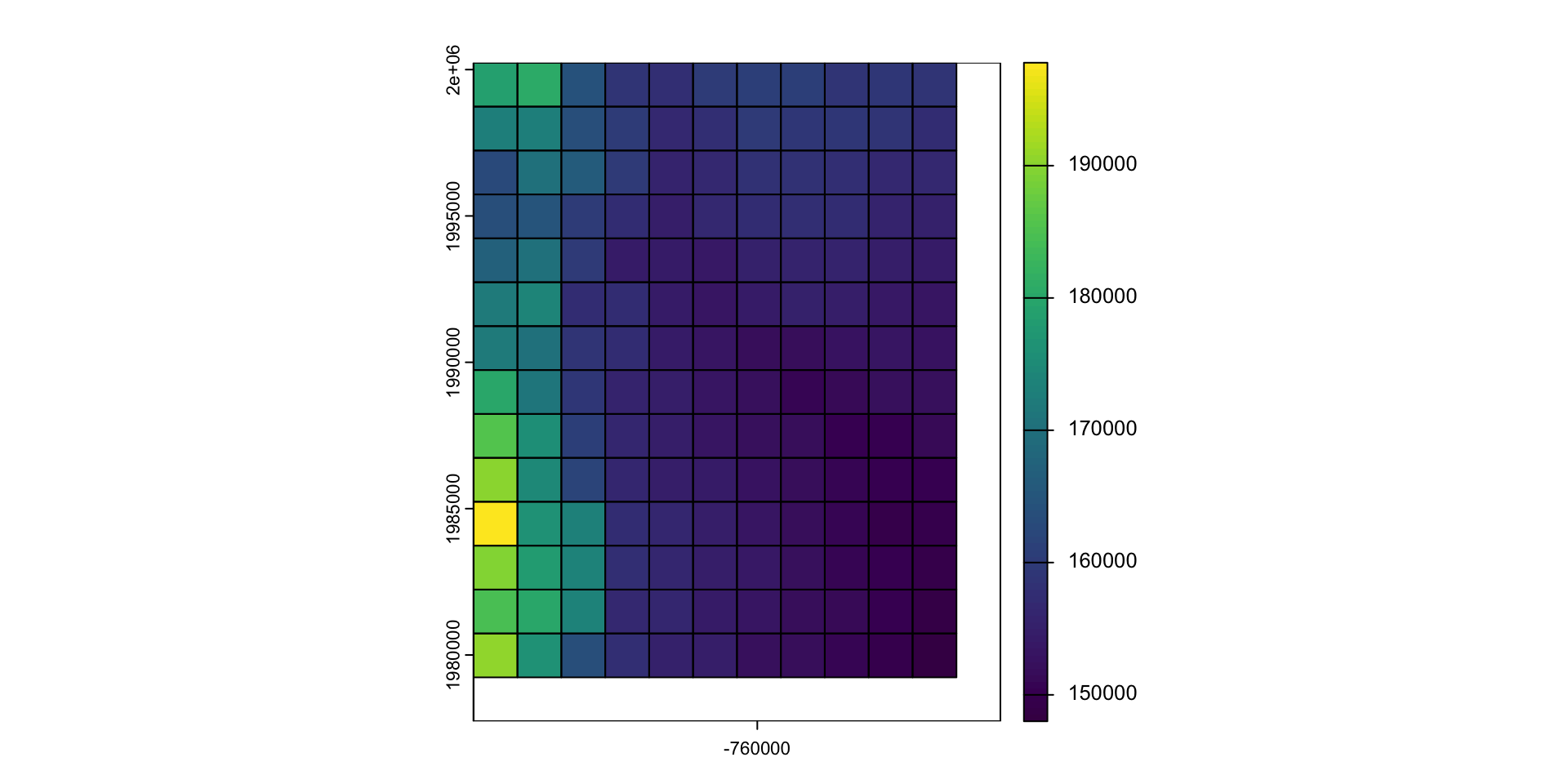
Aggregate and disaggregate

aggregate and disaggregate allow for changing the resolution of a Raster object.
This is similar to the zoom scaling on a web map except the scale factor is not set to 2
For aggregate, you need to specify a function determining what to do with the grouped cell values (default = mean).

plot(fc_elev)
plot(rpoly, add = T)

agg = aggregate(fc_elev, 50, fun = max) #<<
plot(agg)
plot(rpoly, add = T)

`app`

Just like a vector, we can apply functions over a raster with app
These types of formulas are very useful for thresholding analysis
These types of functions are very simular in concept to map_*

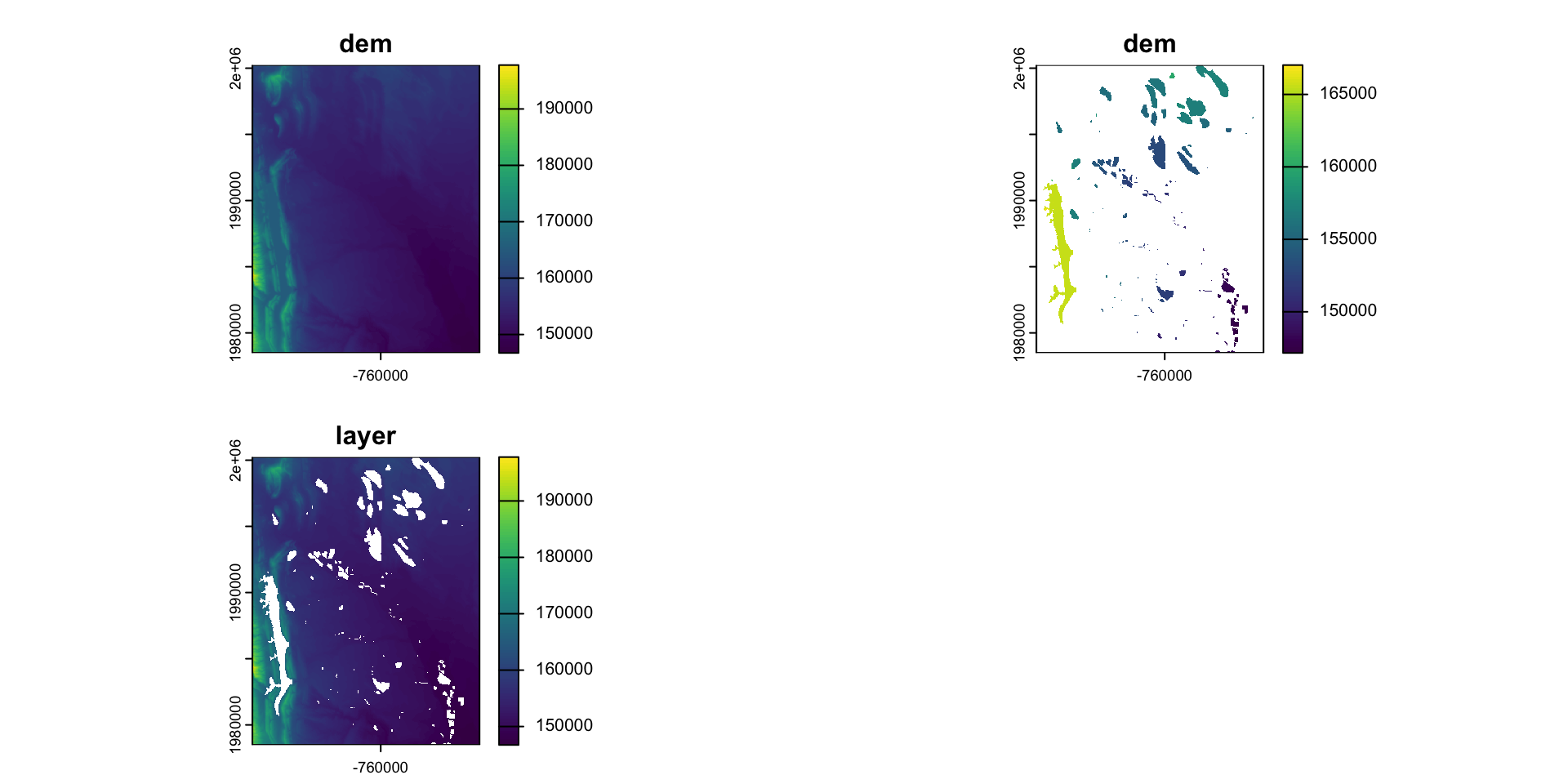
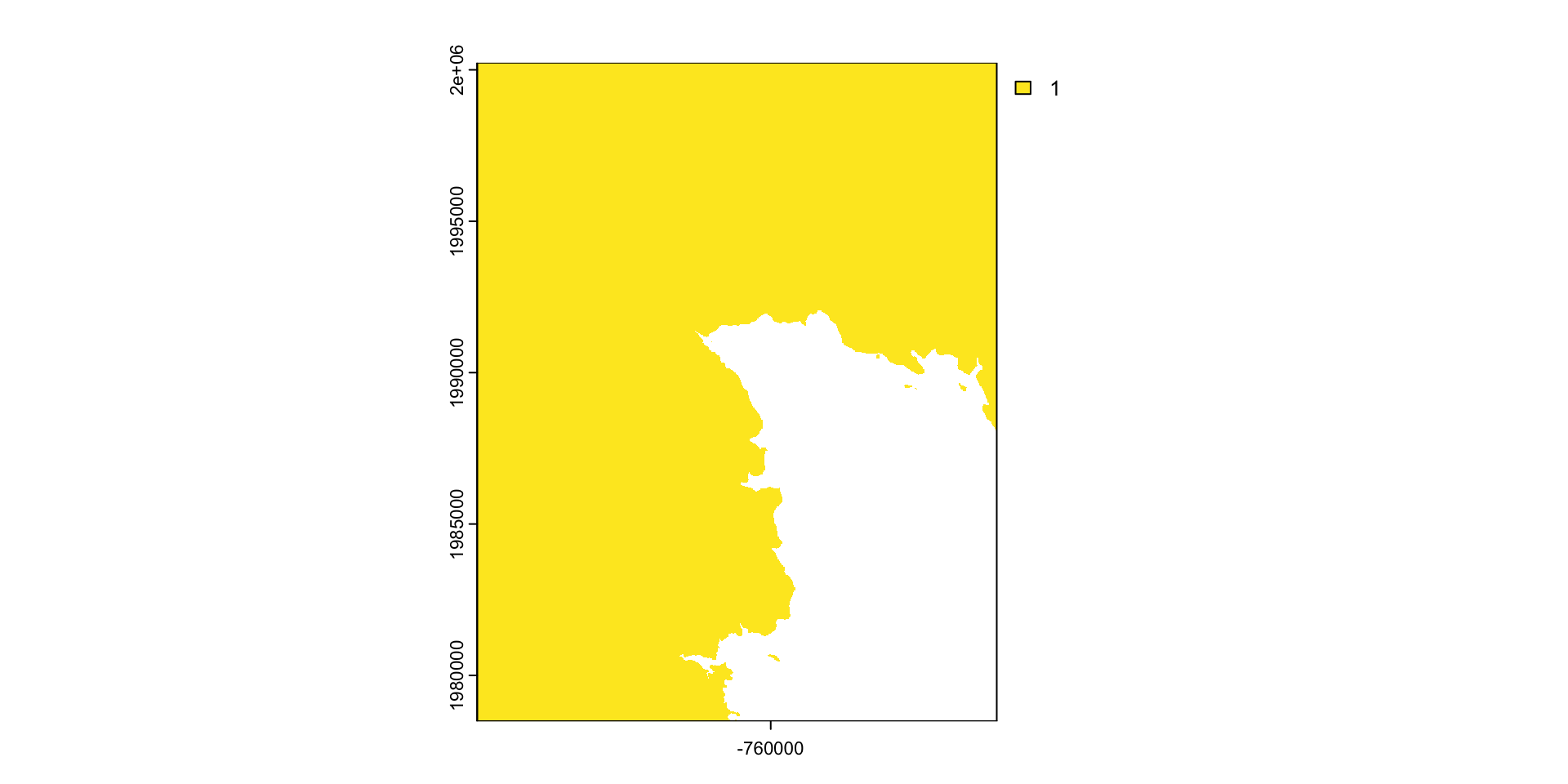
Question: separate Fort Collins into the higher and lower elevations

FUN = function(x){ ifelse(x < mean(x), 1, 2) }

elev3 = app(elev, FUN) #<<
plot(elev3, col = c("red", "blue"))

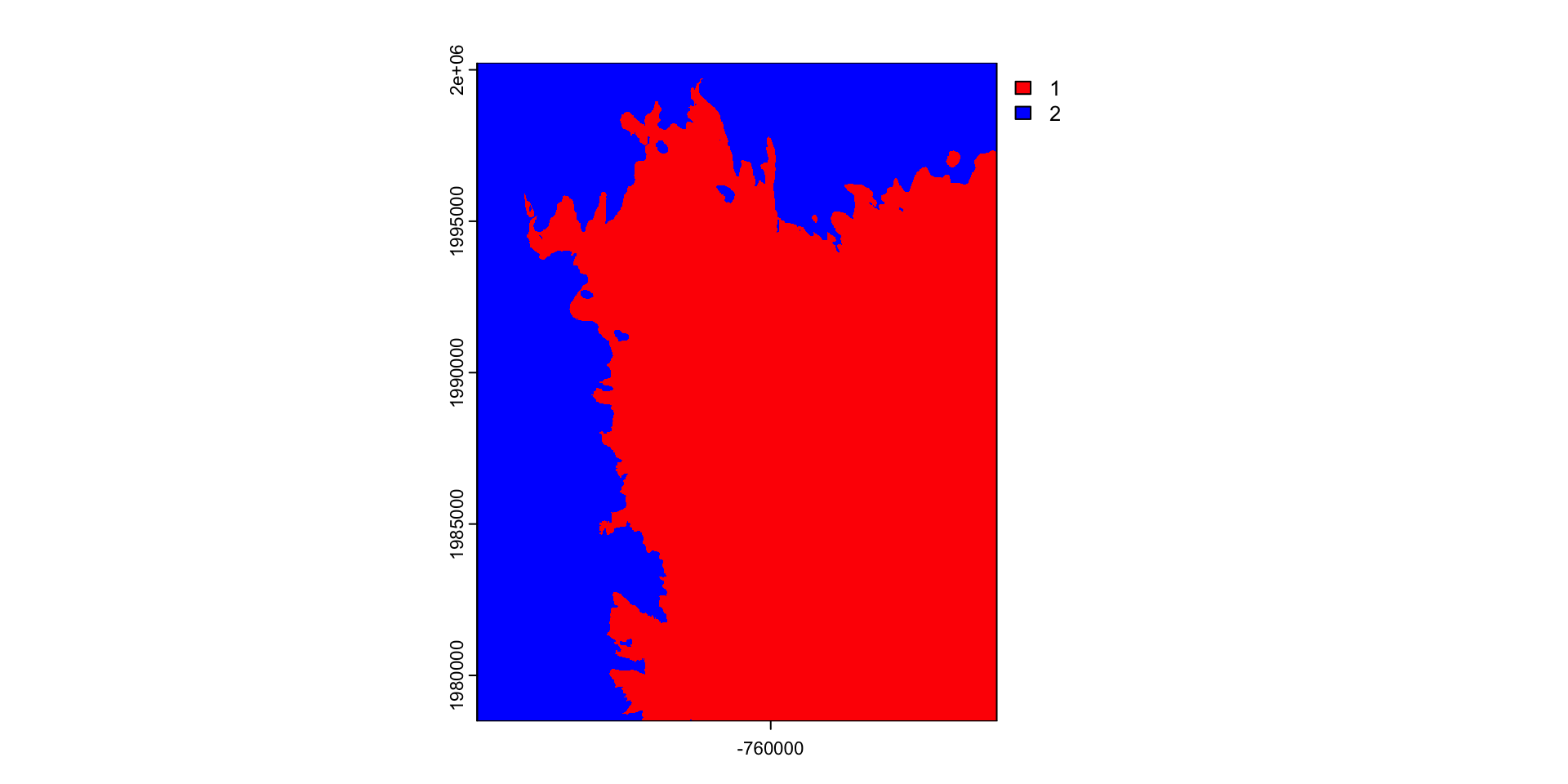
Create a conditional (threshold) mask

threshold = function(x) {ifelse(x <= 152000 , NA, 1)}

threshold(160000)
#> [1] 1
threshold(-10000)
#> [1] NA

r = rast("data/foco-elev.tif")
(m = app(r, threshold))
#> class       : SpatRaster 
#> dimensions  : 725, 572, 1  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : -769695, -752535, 1978485, 2000235  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs 
#> source(s)   : memory
#> name        : lyr.1 
#> min value   :     1 
#> max value   :     1

Results

plot(r)

plot(m)

Multiply cell-wise

algebraic, logical, and functional operations act on a raster cell-wise

elev_cut = m * r
plot(elev_cut, col = viridis::viridis(256))

Reclassify

Reclassify is a function that allows you to change the values of a raster based on a set of rules
The rules are defined in a data frame with three columns:
- min = the minimum value of the range
- max = the maximum value of the range
- lab = the new value to assign to that range

(rcl = data.frame(min = seq(140000,190000,10000), max =  seq(150000,200000,10000), lab = c(0:5)))
#>      min    max lab
#> 1 140000 150000   0
#> 2 150000 160000   1
#> 3 160000 170000   2
#> 4 170000 180000   3
#> 5 180000 190000   4
#> 6 190000 200000   5

(rc = classify(r, rcl, include.lowest = TRUE))
#> class       : SpatRaster 
#> dimensions  : 725, 572, 1  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : -769695, -752535, 1978485, 2000235  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs 
#> source(s)   : memory
#> varname     : foco-elev 
#> name        : dem 
#> min value   :   0 
#> max value   :   5

(s = c(r, m, elev_cut, rc) |> 
  setNames(c("DEM", "Mask", "Elevation Band", "Classified")))
#> class       : SpatRaster 
#> dimensions  : 725, 572, 4  (nrow, ncol, nlyr)
#> resolution  : 30, 30  (x, y)
#> extent      : -769695, -752535, 1978485, 2000235  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=aea +lat_0=23 +lon_0=-96 +lat_1=29.5 +lat_2=45.5 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs 
#> sources     : foco-elev.tif  
#>               memory  
#>               memory  
#>               memory  
#> names       :    DEM, Mask, Elevation Band, Classified 
#> min values  : 146730,    1,         152001,          0 
#> max values  : 197781,    1,         197781,          5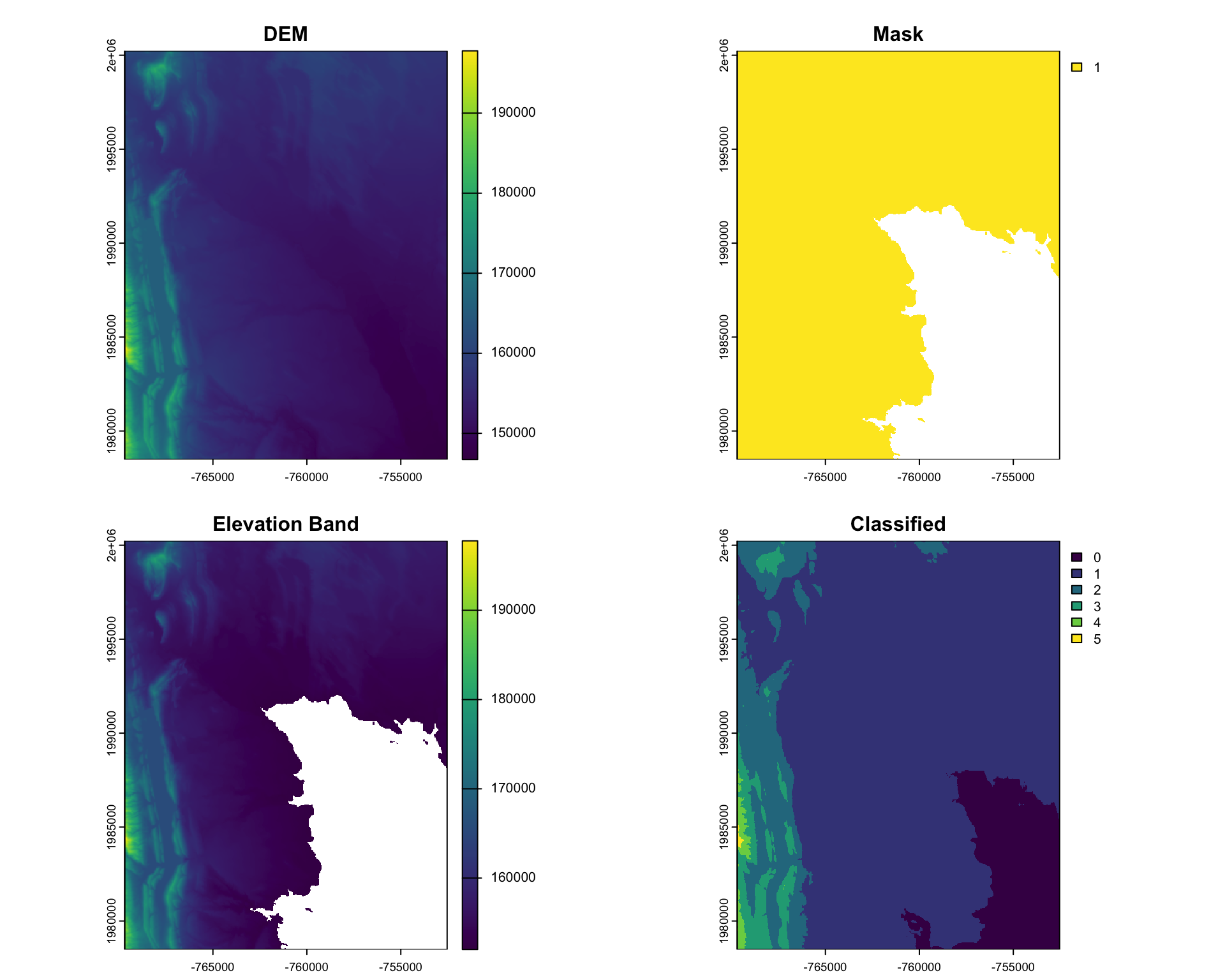

plot(s, col = viridis::viridis(256))

Real Example: Classify Rainfall Regions of Colorado

#remotes::install_github("mikejohnson51/climateR")
library(climateR)
#> 
#> Attaching package: 'climateR'
#> The following object is masked from 'package:readr':
#> 
#>     parse_date
#> The following object is masked from 'package:graphics':
#> 
#>     plot
#> The following object is masked from 'package:base':
#> 
#>     plot

AOI = AOI::aoi_get(state = 'CO') 

system.time({ prcp = climateR::getTerraClim(AOI, 
                                            varname = "ppt", 
                                            startDate = "2000-01-01", 
                                            endDate = '2005-12-31') })
#>    user  system elapsed 
#>   0.354   0.039   2.605

# More on global next time ...
quarts = fivenum(values(mean(prcp$ppt)), na.rm = TRUE)

(rcl = data.frame(quarts[1:4], quarts[2:5], 1:4))
#>   quarts.1.4. quarts.2.5. X1.4
#> 1    15.40274    26.31781    1
#> 2    26.31781    29.69726    2
#> 3    29.69726    33.91096    3
#> 4    33.91096    81.46712    4

(cl_ppt = classify(mean(prcp$ppt), rcl, include.lowest=TRUE))
#> class       : SpatRaster 
#> dimensions  : 99, 170, 1  (nrow, ncol, nlyr)
#> resolution  : 0.04166669, 0.0416667  (x, y)
#> extent      : -109.0833, -102, 36.95833, 41.08334  (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=longlat +ellps=WGS84 +no_defs 
#> source(s)   : memory
#> name        : mean 
#> min value   :    1 
#> max value   :    4

Plot

plot(cl_ppt,col = blues9)
plot(AOI::aoi_get(state = 'CO', county = "all")$geometry, add = TRUE)

Object/Field Interaction

Often, we want to know the relationship between a raster and a vector object
In these cases, we can use the extract function to get values of a raster at the locations (point or bounds) of a vector object
For this example, we will use OpenStreetMap data to get the location of rivers in Fort Collins.

foco_rivers <- osmdata::opq(st_bbox(st_transform(fc,4326))) |> 
  add_osm_feature("waterway") |> 
  osmdata_sf()

Lets find the longest river segment IN our extent

river = foco_rivers$osm_lines |> 
  st_transform(crs(r)) |> 
  st_intersection(st_as_sfc(st_bbox(r))) %>% 
  mutate(length = st_length(.)) |> 
  slice_max(length, n = 1)

plot(r)
plot(river, add = TRUE, col = "blue", lwd = 2)

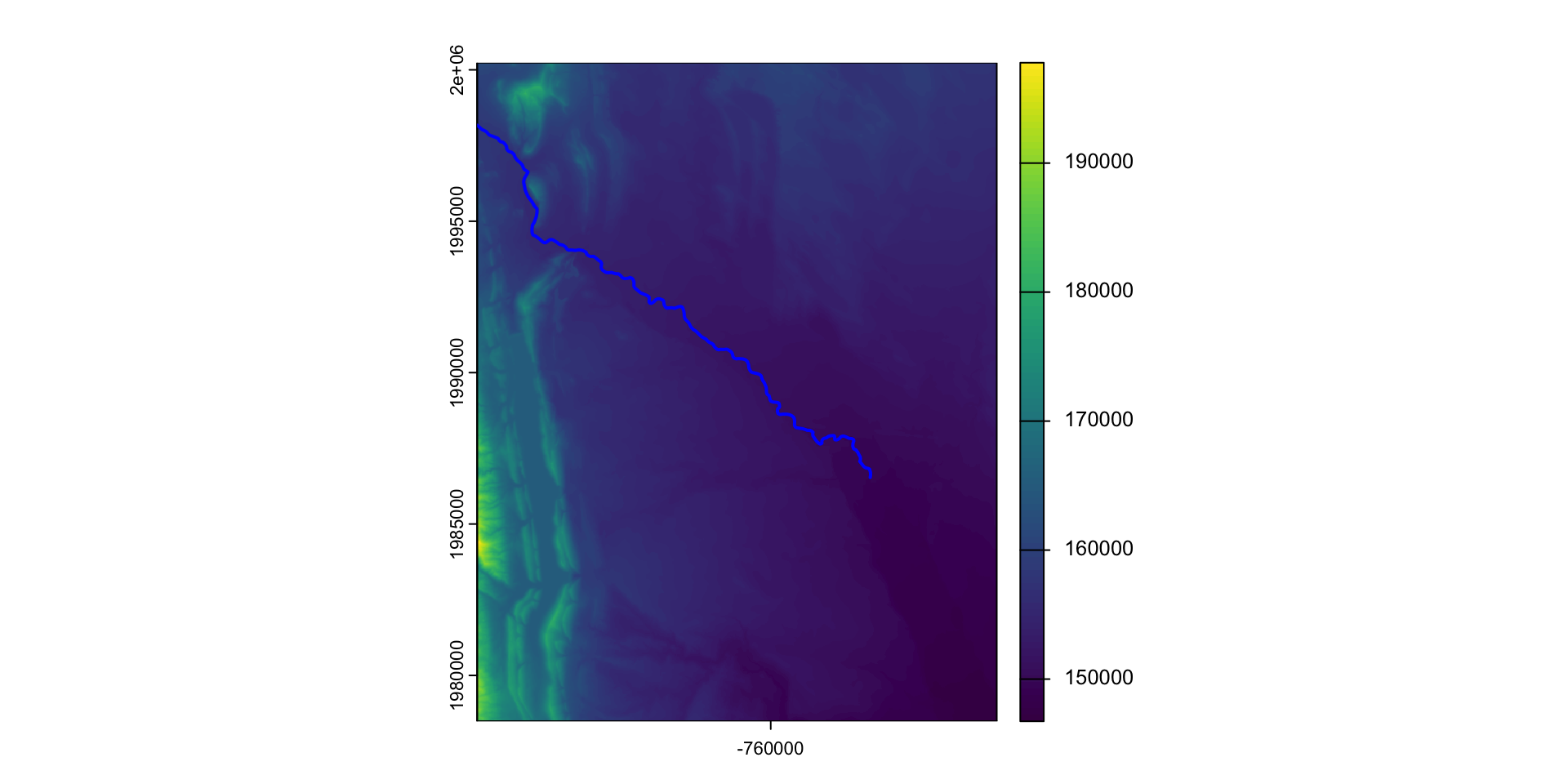
Value Extraction

Often, we want to know the profile and sinousity of a river
To do this, we need to know the inlet and outlet as well as the straight line connector

inlet  = head(st_cast(river, "POINT"), 1)
outlet = tail(st_cast(river, "POINT"), 1) 
pts    = bind_rows(inlet, outlet) 

line = st_cast(st_union(pts), "LINESTRING")

plot(r)
plot(river, add = TRUE, col = "blue", lwd = 2)
plot(line, add = TRUE, col = "black", lwd = 2)
plot(outlet$geom, add = TRUE, pch = 16, col = "red")
plot(inlet$geom,  add = TRUE, pch = 16, col = "green")

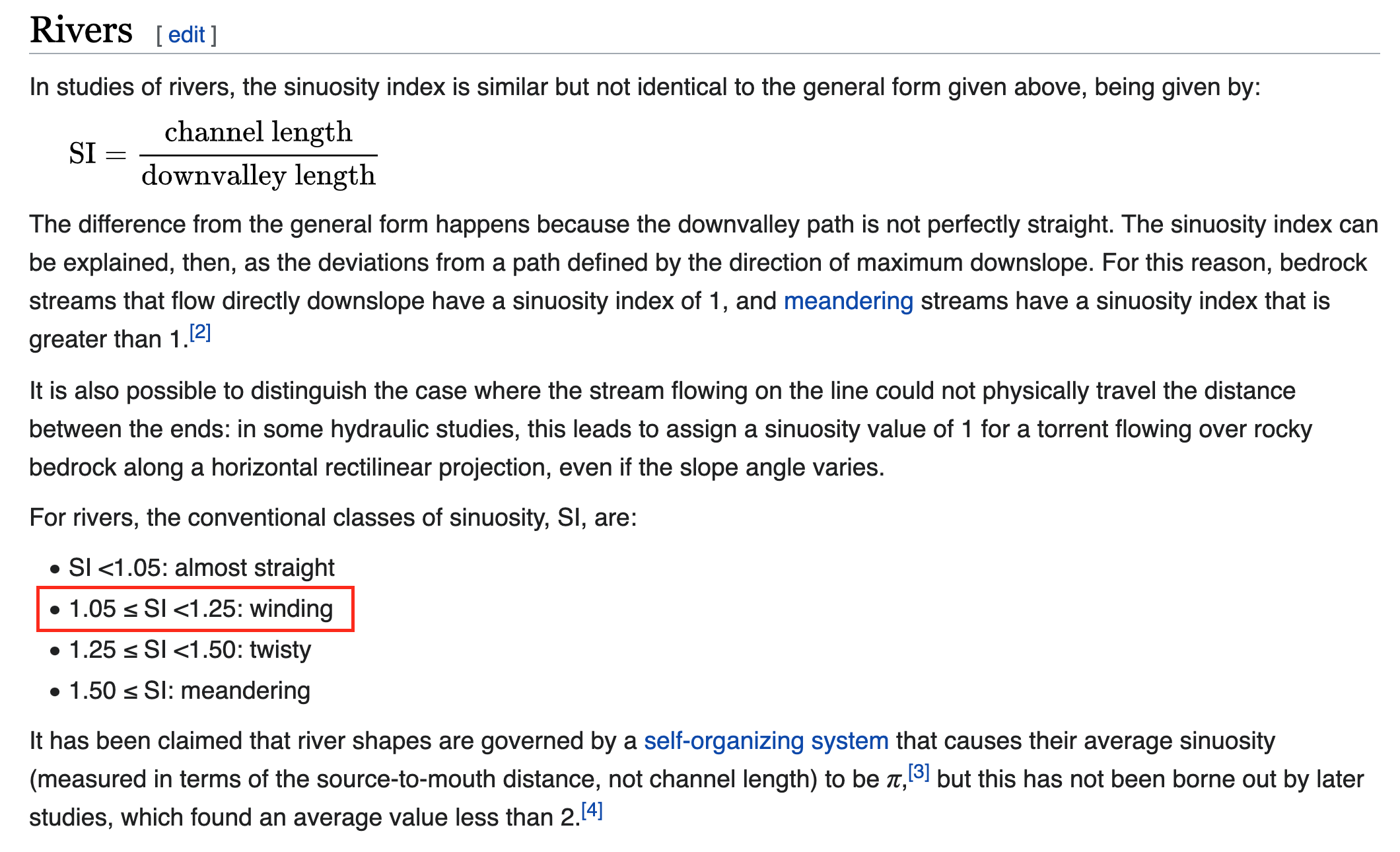
Computation 1: Sinuosity

Channel sinuosity is calculated by dividing the length of the stream channel by the straight line distance between the end points of the selected channel reach.

(sin = st_length(river) / st_length(line))
#> 1.229706 [1]

Computation 1: River Slope

The change in elevation between the inlet/outlet divided by the length (rise/run) give us the slope of the river:

To calculate this, we must extract elevation values at the inlet and outlet:

(elev = extract(r, pts))
#>   ID    dem
#> 1  1 157900
#> 2  2 149284

100 * (elev$dem[1] - elev$dem[2]) / units::drop_units(st_length(river))
#> [1] 40.195

Computation 3: River Profile

The river profile is the elevation of the river at each point along the river.

profile <- extract(r, river)$dem

plot(profile, type = "l")
lines(zoo::rollmean(profile, k = 10),  col = "darkred", lwd = 3)

Assignment

This is your final assignment of the semester and is a 2 day assignment.

Define River Object

We we extract a river profile from the Poudre River in Fort Collins, CO.

To do use the code from lecture to extract all waterways from OpenStreetMap for the Bounding Box of Fort Collins, CO.
Filter the osm_lines object to only include the Cache la Poudre River and merge the lines into a single line object with st_union(). Be sure to convert the object to a sf object with st_as_sf() when done.
Use st_length() to compute the length of the river for future calculations.
Use st_cast() to convert the river object to a POINT object and save it as poudre_pts for latter extraction tasks

Define DEM Object

Use the rast() function to read in the DEM file from the lynker-spatial S3 bucket shared in last assignment. Be sure to use the vsis3 prefix!

Assignment

Extract River Profile

Use the extract() function to extract the elevation values from the DEM at the points along the river.
Use bind_cols() to combine the spatial river points with the extracted elevation values.
Use mutate() to add a new column called ID that is a sequence from 1 to the number of points in the river (n()).

Compute Sinuosity

Use the st_distance() function to compute the straight line distance between the first and last points in the river.
Divide the length of the full river (step 3) by this straight line distance to get the sinuosity. Report the value and what it means. Does this value make sense with respect to the complete Poudre River?

Compute Slope

The slope of a river is the change in elevation between the inlet and outlet divided by the length of the river. Compute this value and report it. Remember the units of the elevation (cm) and of your length!

Assignment

Map Profile: 2 ways

Last, we want to visualize the river profile.

Use ggplot() to create a line plot of the elevation values along the river. Be sure to use the ID column as the x-axis and the dem column as the y-axis. Add nice lables and themese to your chart.
Use ggplot() to plot the spatial mpa of the river profile. Use the geom_sf() function to plot the river and color it by elevation. Be sure to use a nice color scale and theme.

Convert all of this into a Quarto document and submit a link to the deployed document on GitHub to the Canvas.

Congrats!

Lecture 27

Core Raster Principles

1. Extent

2. Discretization

3. CRS

Values

So,

General Process

Find elevation data for Fort Collins:

Raster Values

Raster Values

All image files are the same!

Raster Algebra

Raster Algebra

For example:

Replacement

Modifying a raster

Modifying the underlying data:

What is mask doing?

Crop or/and mask

Aggregate and disaggregate

app

Create a conditional (threshold) mask

Results

Multiply cell-wise

Reclassify

Real Example: Classify Rainfall Regions of Colorado

Plot

Object/Field Interaction

Lets find the longest river segment IN our extent

Value Extraction

Computation 1: Sinuosity

Computation 1: River Slope

Computation 3: River Profile

Assignment

Define River Object

Define DEM Object

Assignment

Extract River Profile

Compute Sinuosity

Compute Slope

Assignment

Map Profile: 2 ways

What is `mask` doing?

`app`