Week 7
Timeseries and Prediction
Learning Objectives
By the end of this lecture, you should be able to:
- Understand what time series data is and why it’s useful
- Work with date and time objects in R
- Load and visualize time series data in R
- Apply basic time series operations: decomposition, smoothing, and forecasting
- Use
ts,zoo, andxtsobjects for time-indexed data - Understand tidy approaches using
tsibbleandfeasts - Recognize real-world environmental science applications of time series
What is Time Series Data?
Time series data is a collection of observations recorded sequentially over time. Unlike other data types, time series data is ordered, and that order carries critical information.
Examples:
- Streamflow measurements (e.g., daily CFS at a USGS gage)
- Atmospheric CO₂ levels (e.g., Mauna Loa Observatory)
- Snowpack depth over time
- Urban water consumption by month
Why Time Series Matter
Time series analysis helps us:
- Understand trends and patterns
- Detect anomalies (e.g., droughts, sensor failures)
- Forecast future values (e.g., streamflow, temperature)
Working with Date Objects in R
Time series analysis depends on accurate and well-formatted date/time information.
Before we can analyis time series data, we need to understand how R handles dates and times.
R has built-in classes for date and time objects, which are essential for time series analysis.
Base R Date Functions
R has several native classes for handling dates and times:
- Date: Date object
- POSIXct: Date and time
- POSIXlt: List of date and time components
Date Sequences
You can create sequences of dates using the seq.Date() function:
from: Start dateto: End date (optional)by: Interval (e.g., “day”, “month”, “year”)length.out: Number of dates to generate
You can also use seq() to create sequences of POSIXct/lt objects:
from: Start date/timeto: End date/time (optional)by: Interval (e.g., “hour”, “minute”, “second”)length.out: Number of dates to generate
seq(from = as.POSIXct("2024-01-01 00:00"),
to = as.POSIXct("2024-01-02 00:00"),
by = "hour")
#> [1] "2024-01-01 00:00:00 MST" "2024-01-01 01:00:00 MST"
#> [3] "2024-01-01 02:00:00 MST" "2024-01-01 03:00:00 MST"
#> [5] "2024-01-01 04:00:00 MST" "2024-01-01 05:00:00 MST"
#> [7] "2024-01-01 06:00:00 MST" "2024-01-01 07:00:00 MST"
#> [9] "2024-01-01 08:00:00 MST" "2024-01-01 09:00:00 MST"
#> [11] "2024-01-01 10:00:00 MST" "2024-01-01 11:00:00 MST"
#> [13] "2024-01-01 12:00:00 MST" "2024-01-01 13:00:00 MST"
#> [15] "2024-01-01 14:00:00 MST" "2024-01-01 15:00:00 MST"
#> [17] "2024-01-01 16:00:00 MST" "2024-01-01 17:00:00 MST"
#> [19] "2024-01-01 18:00:00 MST" "2024-01-01 19:00:00 MST"
#> [21] "2024-01-01 20:00:00 MST" "2024-01-01 21:00:00 MST"
#> [23] "2024-01-01 22:00:00 MST" "2024-01-01 23:00:00 MST"
#> [25] "2024-01-02 00:00:00 MST"Timezones
By default, R uses the system’s timezone.
The
Sys.timezone()function returns the current timezone.If you want to use anthor timezone, say GMT/UTC, you can change it:
lubridate Package ![]()
The
lubridatepackage comes with thetidyverseand is designed to make working with dates and times easier.It provides a consistent set of functions for parsing, manipulating, and formatting date-time objects.
Use lubridate to handle inconsistent formats and to align data with time zones, daylight savings, etc.
lubridate timezones ![]()
lubridate also provides functions for working with time zones. You can convert between time zones using with_tz() and force_tz().
(date <- ymd_hms("2024-04-08 14:30:00", tz = "America/New_York"))
#> [1] "2024-04-08 14:30:00 EDT"
# Change time zone without changing time
force_tz(date, "America/Los_Angeles")
#> [1] "2024-04-08 14:30:00 PDT"
# Convert to another timezone
with_tz(date, "America/Los_Angeles")
#> [1] "2024-04-08 11:30:00 PDT"R Packages for Time Series
R has several packages/systme for time series analysis, including:
ts: Base R time series classzoo: Provides a flexible class for ordered observationsxts: Extensible time series class for irregularly spaced dataforecast: Functions for forecasting time series datatsibble: Tidy time series data framesfeasts: Functions for time series analysis and visualizationmodeltime: Time series modeling with tidymodels
When to Use Which Time Series Format?
| Format | Best For | Advantages | Limitations |
|---|---|---|---|
ts |
Regular, simple time series | Built into base R, supported by forecast |
Rigid time format, inflexible for joins |
zoo |
Irregular time steps | Arbitrary index, supports irregular data | More complex syntax |
xts |
Financial-style or irregular data | Good for date-time indexing and joins | More complex to visualize |
tsibble |
Tidyverse workflows | Pipes with dplyr, ggplot2, forecasting with fable |
Requires tsibble structure |
tibble + Date |
General purpose | Flexible, tidy | Needs conversion for time series modeling |
Key Concepts in Time Series
1. Trend: Long-term increase or decrease in the data
2. Seasonality: Repeating short-term cycle (e.g., annual snowmelt)
3. Noise: Random variation
4. Stationarity: Statistical properties (mean, variance) don’t change over time
5. Autocorrelation: Correlation of a time series with its own past values
Introducing the Mauna Loa CO₂ Dataset
Mauna Loa CO₂ Dataset
The
co2dataset is a classic example of time series data. It contains monthly atmospheric CO₂ concentrations measured at the Mauna Loa Observatory in Hawaii.co2is a built-in dataset representing monthly CO₂ concentrations from 1959 onward.
class(co2)
#> [1] "ts"
co2
#> Jan Feb Mar Apr May Jun Jul Aug Sep Oct
#> 1959 315.42 316.31 316.50 317.56 318.13 318.00 316.39 314.65 313.68 313.18
#> 1960 316.27 316.81 317.42 318.87 319.87 319.43 318.01 315.74 314.00 313.68
#> 1961 316.73 317.54 318.38 319.31 320.42 319.61 318.42 316.63 314.83 315.16
#> 1962 317.78 318.40 319.53 320.42 320.85 320.45 319.45 317.25 316.11 315.27
#> 1963 318.58 318.92 319.70 321.22 322.08 321.31 319.58 317.61 316.05 315.83
#> 1964 319.41 320.07 320.74 321.40 322.06 321.73 320.27 318.54 316.54 316.71
#> 1965 319.27 320.28 320.73 321.97 322.00 321.71 321.05 318.71 317.66 317.14
#> 1966 320.46 321.43 322.23 323.54 323.91 323.59 322.24 320.20 318.48 317.94
#> 1967 322.17 322.34 322.88 324.25 324.83 323.93 322.38 320.76 319.10 319.24
#> 1968 322.40 322.99 323.73 324.86 325.40 325.20 323.98 321.95 320.18 320.09
#> 1969 323.83 324.26 325.47 326.50 327.21 326.54 325.72 323.50 322.22 321.62
#> 1970 324.89 325.82 326.77 327.97 327.91 327.50 326.18 324.53 322.93 322.90
#> 1971 326.01 326.51 327.01 327.62 328.76 328.40 327.20 325.27 323.20 323.40
#> 1972 326.60 327.47 327.58 329.56 329.90 328.92 327.88 326.16 324.68 325.04
#> 1973 328.37 329.40 330.14 331.33 332.31 331.90 330.70 329.15 327.35 327.02
#> 1974 329.18 330.55 331.32 332.48 332.92 332.08 331.01 329.23 327.27 327.21
#> 1975 330.23 331.25 331.87 333.14 333.80 333.43 331.73 329.90 328.40 328.17
#> 1976 331.58 332.39 333.33 334.41 334.71 334.17 332.89 330.77 329.14 328.78
#> 1977 332.75 333.24 334.53 335.90 336.57 336.10 334.76 332.59 331.42 330.98
#> 1978 334.80 335.22 336.47 337.59 337.84 337.72 336.37 334.51 332.60 332.38
#> 1979 336.05 336.59 337.79 338.71 339.30 339.12 337.56 335.92 333.75 333.70
#> 1980 337.84 338.19 339.91 340.60 341.29 341.00 339.39 337.43 335.72 335.84
#> 1981 339.06 340.30 341.21 342.33 342.74 342.08 340.32 338.26 336.52 336.68
#> 1982 340.57 341.44 342.53 343.39 343.96 343.18 341.88 339.65 337.81 337.69
#> 1983 341.20 342.35 342.93 344.77 345.58 345.14 343.81 342.21 339.69 339.82
#> 1984 343.52 344.33 345.11 346.88 347.25 346.62 345.22 343.11 340.90 341.18
#> 1985 344.79 345.82 347.25 348.17 348.74 348.07 346.38 344.51 342.92 342.62
#> 1986 346.11 346.78 347.68 349.37 350.03 349.37 347.76 345.73 344.68 343.99
#> 1987 347.84 348.29 349.23 350.80 351.66 351.07 349.33 347.92 346.27 346.18
#> 1988 350.25 351.54 352.05 353.41 354.04 353.62 352.22 350.27 348.55 348.72
#> 1989 352.60 352.92 353.53 355.26 355.52 354.97 353.75 351.52 349.64 349.83
#> 1990 353.50 354.55 355.23 356.04 357.00 356.07 354.67 352.76 350.82 351.04
#> 1991 354.59 355.63 357.03 358.48 359.22 358.12 356.06 353.92 352.05 352.11
#> 1992 355.88 356.63 357.72 359.07 359.58 359.17 356.94 354.92 352.94 353.23
#> 1993 356.63 357.10 358.32 359.41 360.23 359.55 357.53 355.48 353.67 353.95
#> 1994 358.34 358.89 359.95 361.25 361.67 360.94 359.55 357.49 355.84 356.00
#> 1995 359.98 361.03 361.66 363.48 363.82 363.30 361.94 359.50 358.11 357.80
#> 1996 362.09 363.29 364.06 364.76 365.45 365.01 363.70 361.54 359.51 359.65
#> 1997 363.23 364.06 364.61 366.40 366.84 365.68 364.52 362.57 360.24 360.83
#> Nov Dec
#> 1959 314.66 315.43
#> 1960 314.84 316.03
#> 1961 315.94 316.85
#> 1962 316.53 317.53
#> 1963 316.91 318.20
#> 1964 317.53 318.55
#> 1965 318.70 319.25
#> 1966 319.63 320.87
#> 1967 320.56 321.80
#> 1968 321.16 322.74
#> 1969 322.69 323.95
#> 1970 323.85 324.96
#> 1971 324.63 325.85
#> 1972 326.34 327.39
#> 1973 327.99 328.48
#> 1974 328.29 329.41
#> 1975 329.32 330.59
#> 1976 330.14 331.52
#> 1977 332.24 333.68
#> 1978 333.75 334.78
#> 1979 335.12 336.56
#> 1980 336.93 338.04
#> 1981 338.19 339.44
#> 1982 339.09 340.32
#> 1983 340.98 342.82
#> 1984 342.80 344.04
#> 1985 344.06 345.38
#> 1986 345.48 346.72
#> 1987 347.64 348.78
#> 1988 349.91 351.18
#> 1989 351.14 352.37
#> 1990 352.69 354.07
#> 1991 353.64 354.89
#> 1992 354.09 355.33
#> 1993 355.30 356.78
#> 1994 357.59 359.05
#> 1995 359.61 360.74
#> 1996 360.80 362.38
#> 1997 362.49 364.34Initial Plot
The
co2dataset is a time series object (ts) with 12 observations per year, starting from January 1959.There is a default plot method for
tsobjects that we can take advantage of:
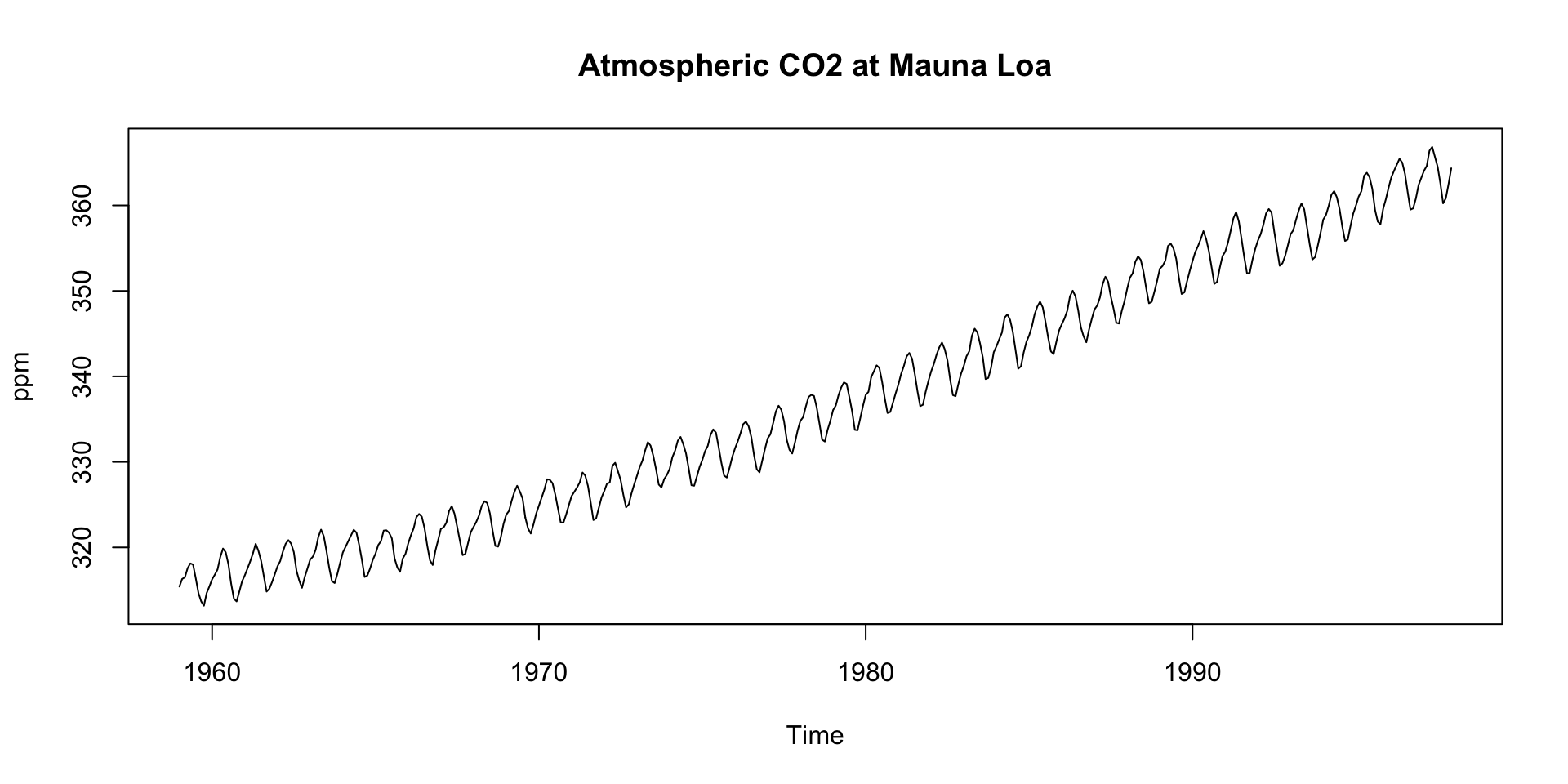
We see:
- An upward trend
- Regular seasonal oscillations (higher in winter, lower in summer)
Understanding ts Objects
You can think of ts objects as numeric vectors with time attributes.
tsobjects are used to represent time series data and are created using thets()function.They have attributes like
start,end, andfrequencythat define the time index.startandenddefine the time range of the data.frequencydefines the number of observations per unit of time (e.g., 12 for monthly data).
Subsetting and Plotting
Like vectors, you can subset
tsobjects using indexing.For example, to extract the first year of data:
- Or, a specific range of years:
window(co2, start = c(1990, 1), end = c(1995, 12))
#> Jan Feb Mar Apr May Jun Jul Aug Sep Oct
#> 1990 353.50 354.55 355.23 356.04 357.00 356.07 354.67 352.76 350.82 351.04
#> 1991 354.59 355.63 357.03 358.48 359.22 358.12 356.06 353.92 352.05 352.11
#> 1992 355.88 356.63 357.72 359.07 359.58 359.17 356.94 354.92 352.94 353.23
#> 1993 356.63 357.10 358.32 359.41 360.23 359.55 357.53 355.48 353.67 353.95
#> 1994 358.34 358.89 359.95 361.25 361.67 360.94 359.55 357.49 355.84 356.00
#> 1995 359.98 361.03 361.66 363.48 363.82 363.30 361.94 359.50 358.11 357.80
#> Nov Dec
#> 1990 352.69 354.07
#> 1991 353.64 354.89
#> 1992 354.09 355.33
#> 1993 355.30 356.78
#> 1994 357.59 359.05
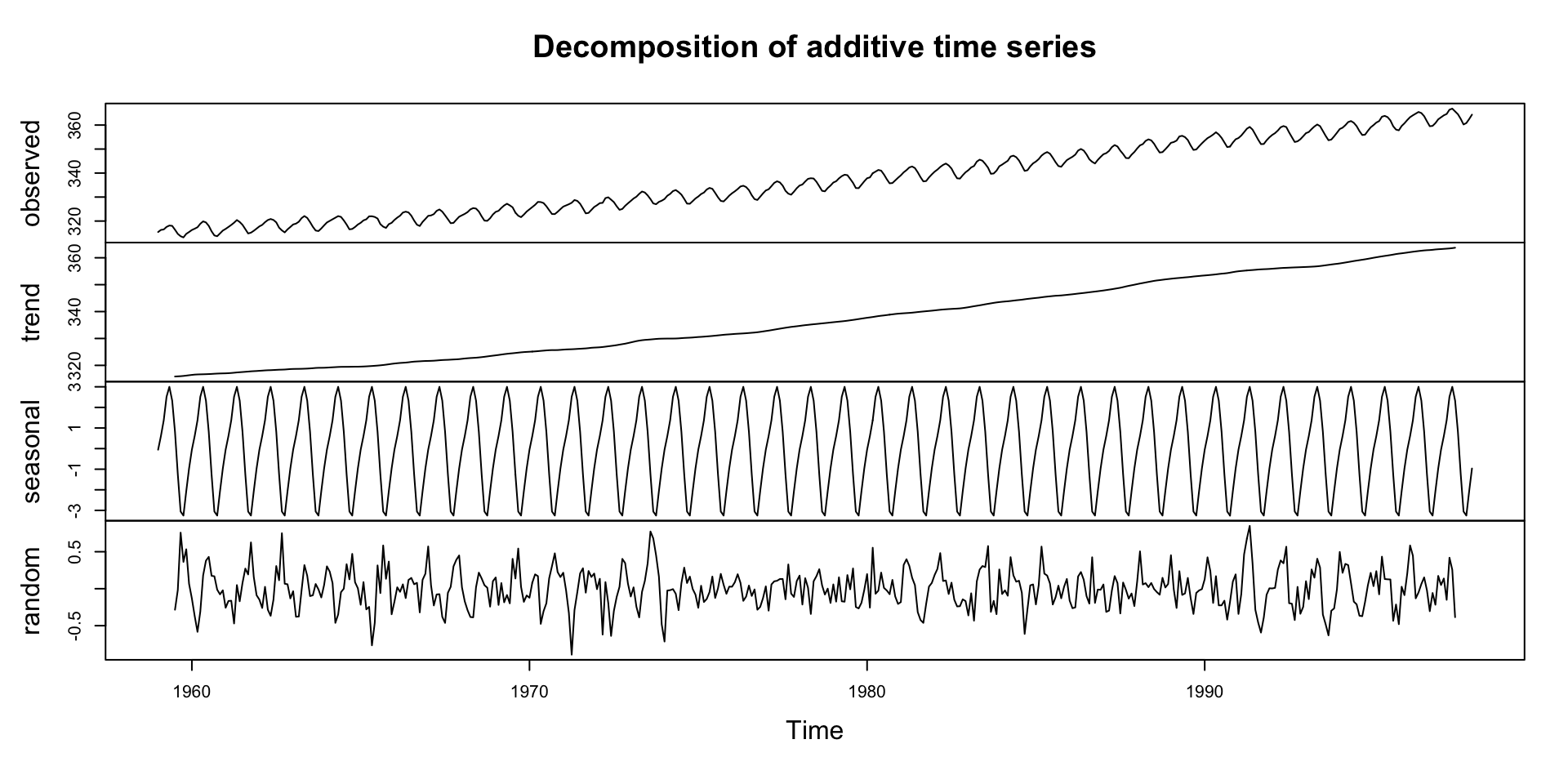
#> 1995 359.61 360.74Decomposing a Time Series
Decomposition is a technique to separate a time series into its components: trend, seasonality, and residuals.
This helps separate structure from noise.
In environmental science, this is useful for:
Removing seasonality to study droughts
Analyzing long-term trends
Understanding seasonal patterns in streamflow
Identifying anomalies in water quality data
Detecting changes in vegetation phenology
Monitoring seasonal patterns in temperature
Analyzing seasonal patterns in water demand
…
What is Decomposition?
Decomposition separates a time series into interpretable components:
- Trend: Long-term movement
- Seasonality: Regular, periodic fluctuations
- Residual/Irregular: Random noise or anomalies
Additive vs Multiplicative
Additive model:
\[ Y_t = T_t + S_t + R_t \]Multiplicative model:
\[ Y_t = T_t \times S_t \times R_t \]
Use additive if seasonal variation is roughly constant.
Use multiplicative if it grows/shrinks with the trend.
Example
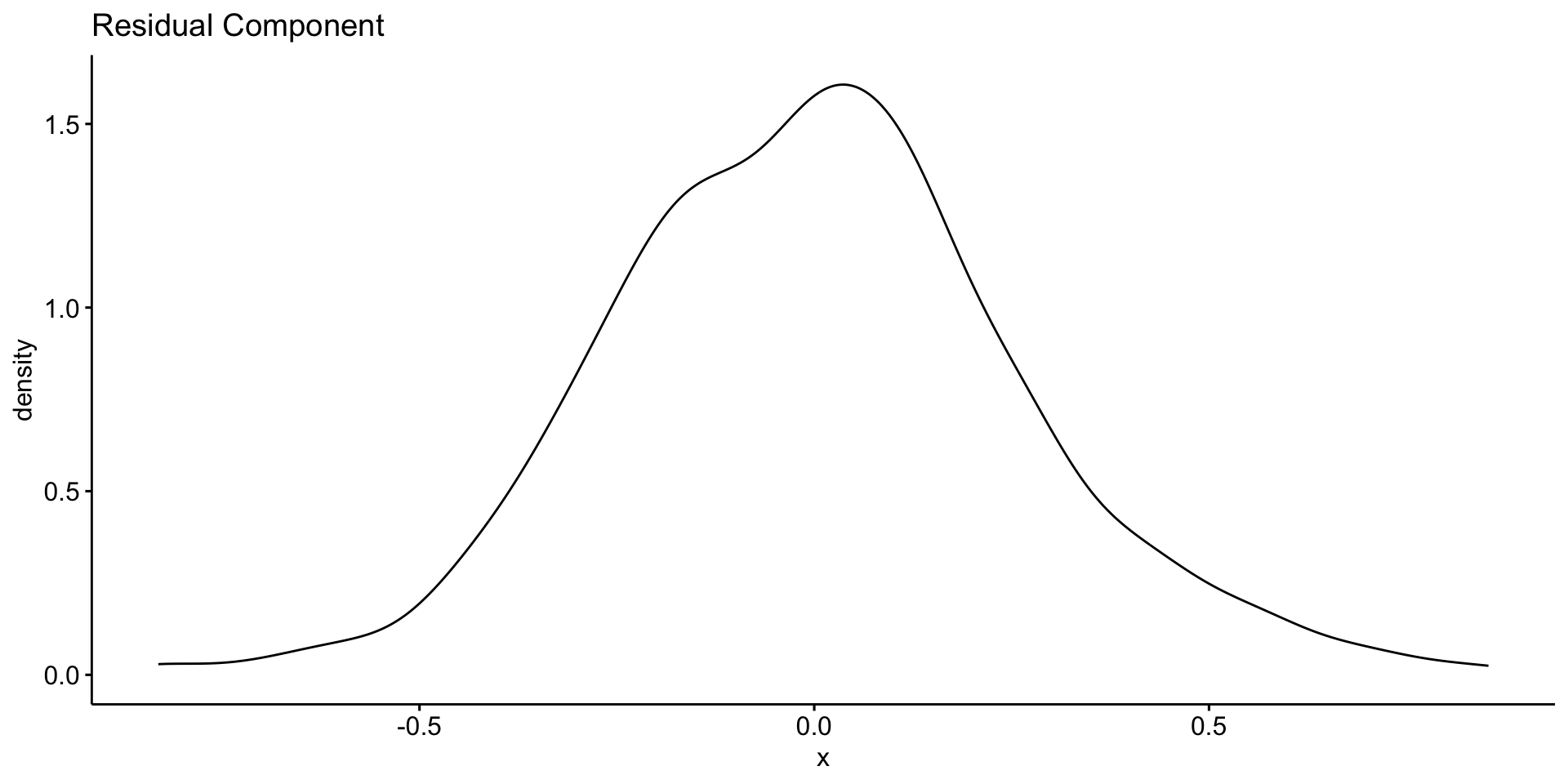
Why Decompose?
Trend: Are CO₂ levels increasing?
Seasonality: Are there predictable cycles each year?
Remainder: What’s left after we remove trend and season? (what is the randomness?)
Decompostion in R
- The
decompose()function in R can be used to perform this operation. - The
decompose()function by default assumes that the time series is additive
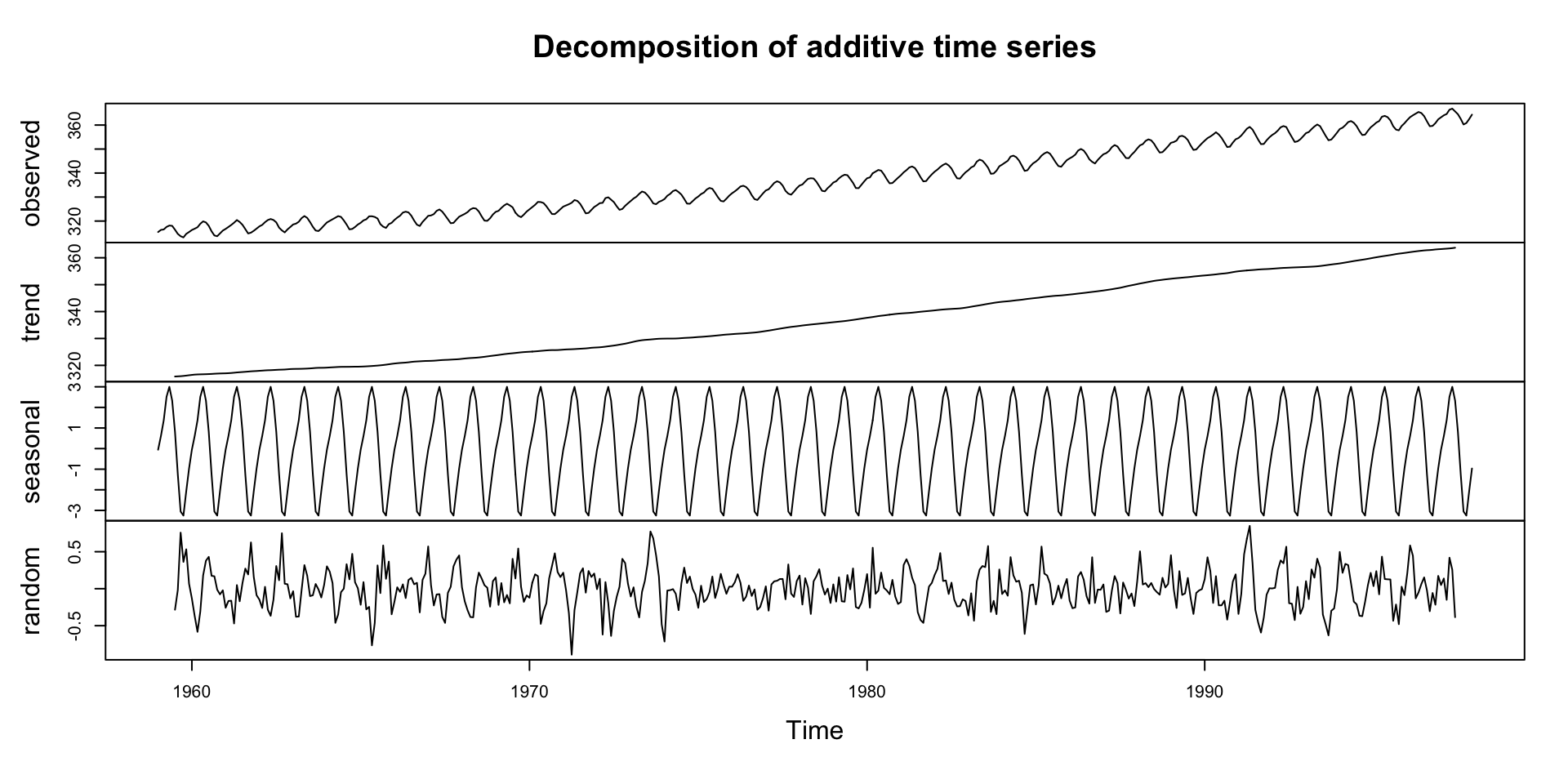
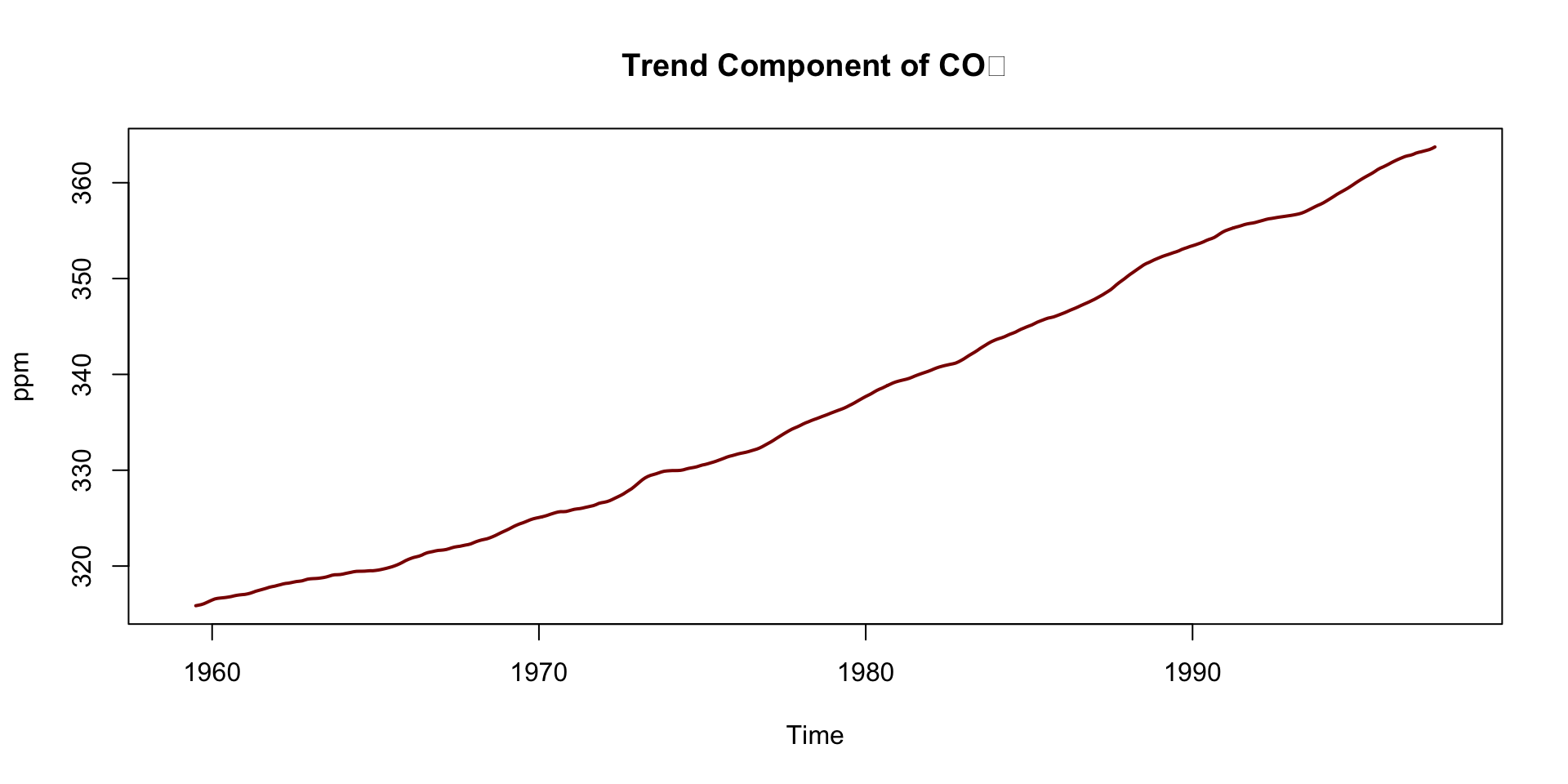
Deep Dive: Trend Component
Steady upward slope from ~316 ppm in 1959 to ~365 ppm in the late 1990s
Captures the long-term forcing from human activity:
- Fossil fuel combustion
- Deforestation
This trend underpins climate change science — known as the Keeling Curve
Notice how the trend smooths short-term fluctuations
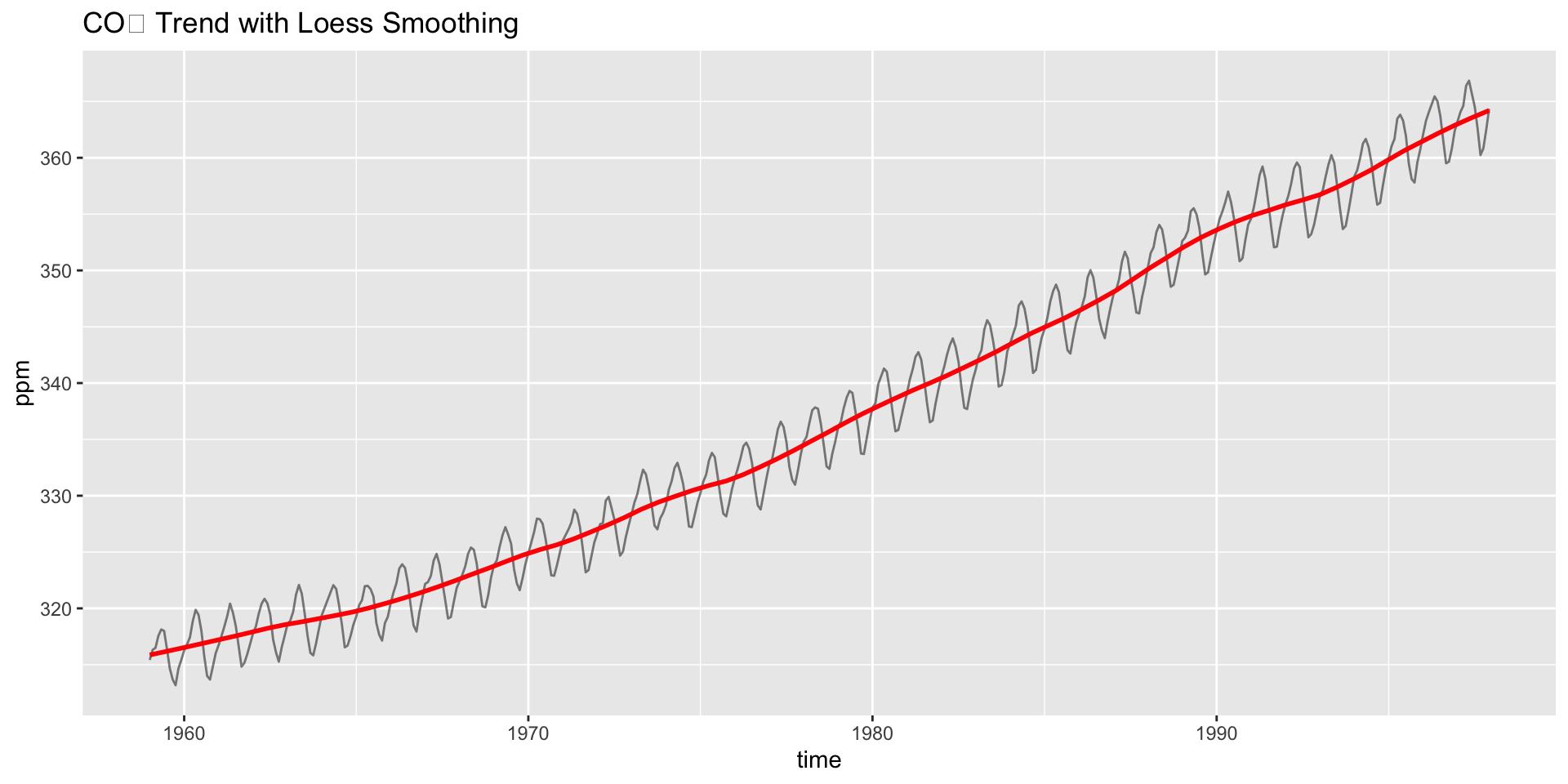
Interpreting the Trend
- A linear model or loess smoother can also help quantify the trend:
co2_df <- data.frame(time = time(co2), co2 = as.numeric(co2))
lm(as.numeric(co2) ~ time(co2)) |>
summary()
#>
#> Call:
#> lm(formula = as.numeric(co2) ~ time(co2))
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -6.0399 -1.9476 -0.0017 1.9113 6.5149
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -2.250e+03 2.127e+01 -105.8 <2e-16 ***
#> time(co2) 1.308e+00 1.075e-02 121.6 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.618 on 466 degrees of freedom
#> Multiple R-squared: 0.9695, Adjusted R-squared: 0.9694
#> F-statistic: 1.479e+04 on 1 and 466 DF, p-value: < 2.2e-16Do you see acceleration in the rise over time?
De-Trending
- Detrending is the process of removing the trend component from a time series.
- This can help for modeling the trend + residual only:
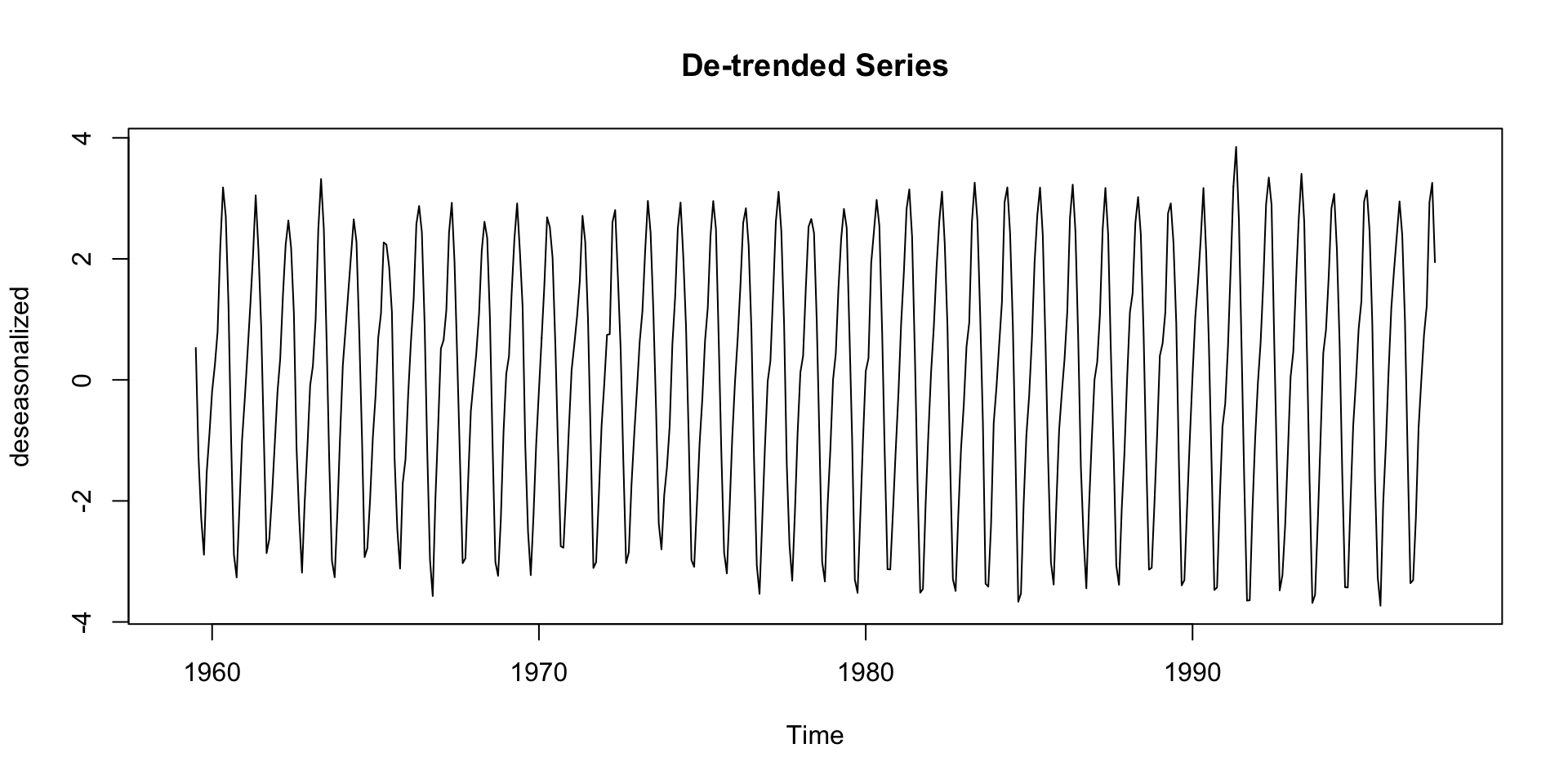
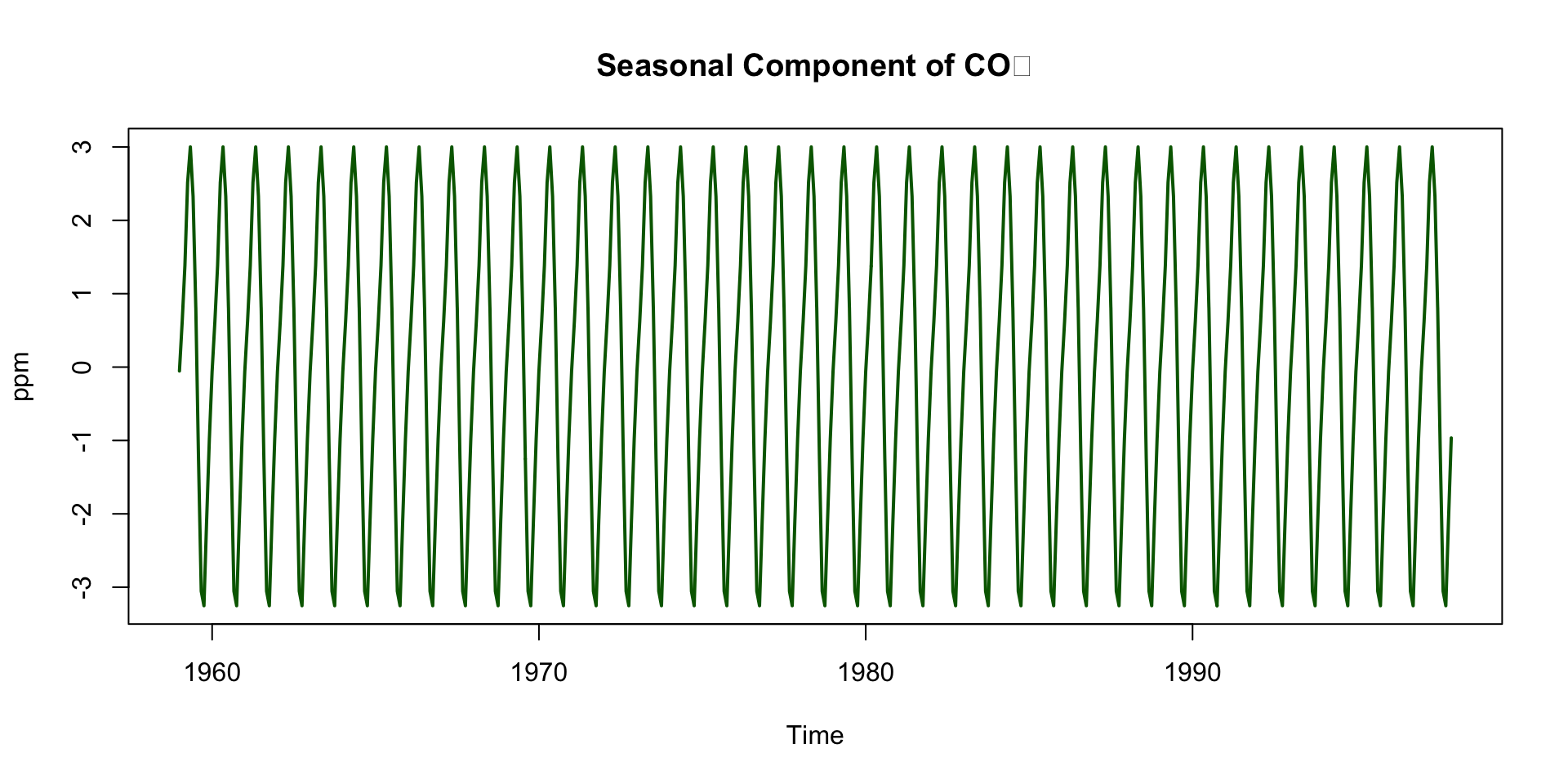
Deep Dive: Seasonal Component
Repeats every 12 months
Peaks around May, drops in September–October
Driven by biospheric fluxes:
- Photosynthesis during spring/summer → CO₂ drawdown
- Decomposition and respiration in winter → CO₂ release
Seasonal Cycle is Northern Hemisphere-Dominated (Mauna Loa is in the Northern Hemisphere)
Northern Hemisphere contains more landmass and vegetation
So its biosphere exerts a stronger influence on global CO₂ than the Southern Hemisphere
This explains the pronounced seasonal cycle in the signal
De-seasonalizing
This can help for modeling the seasonal + residual only:
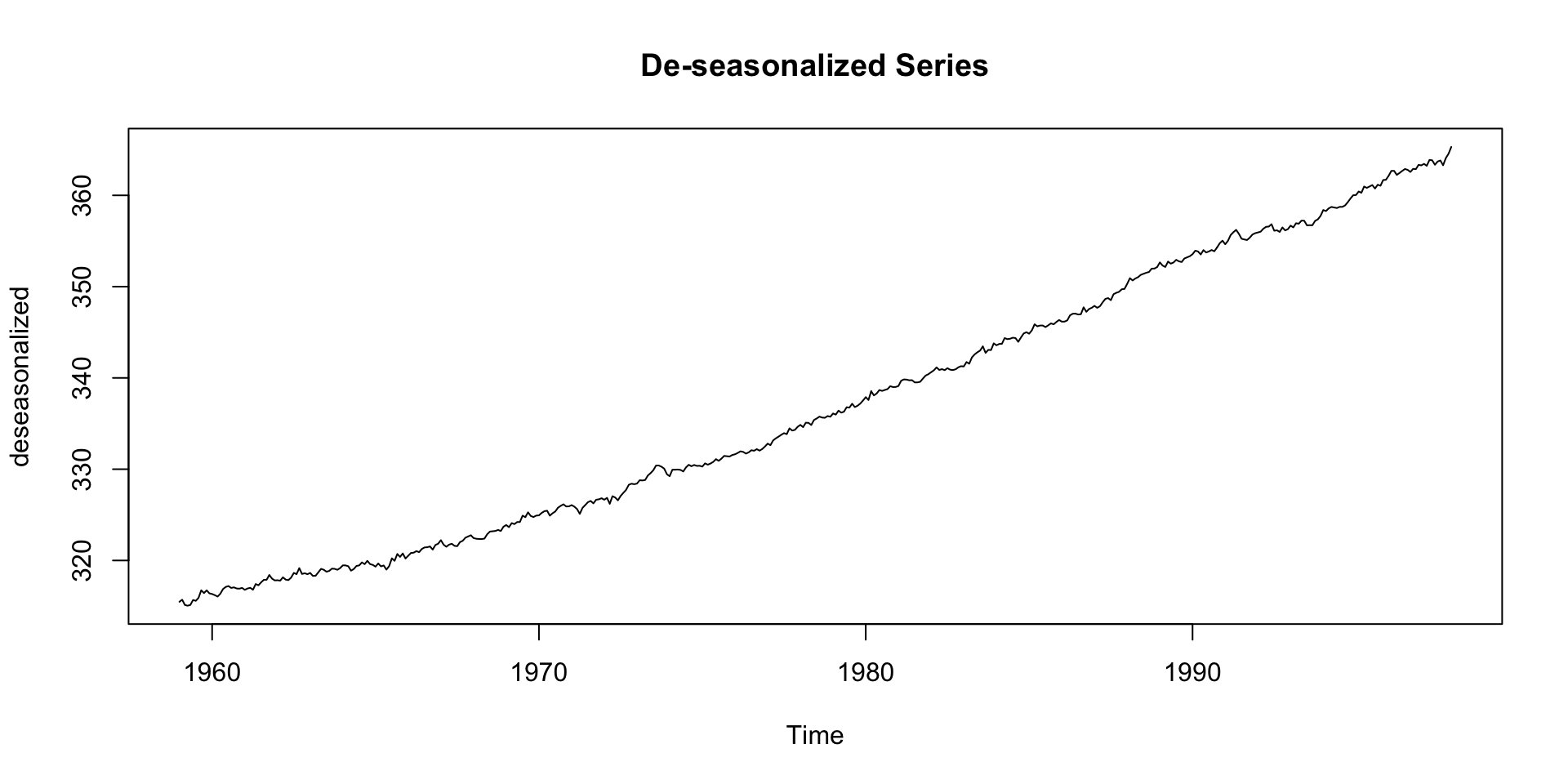
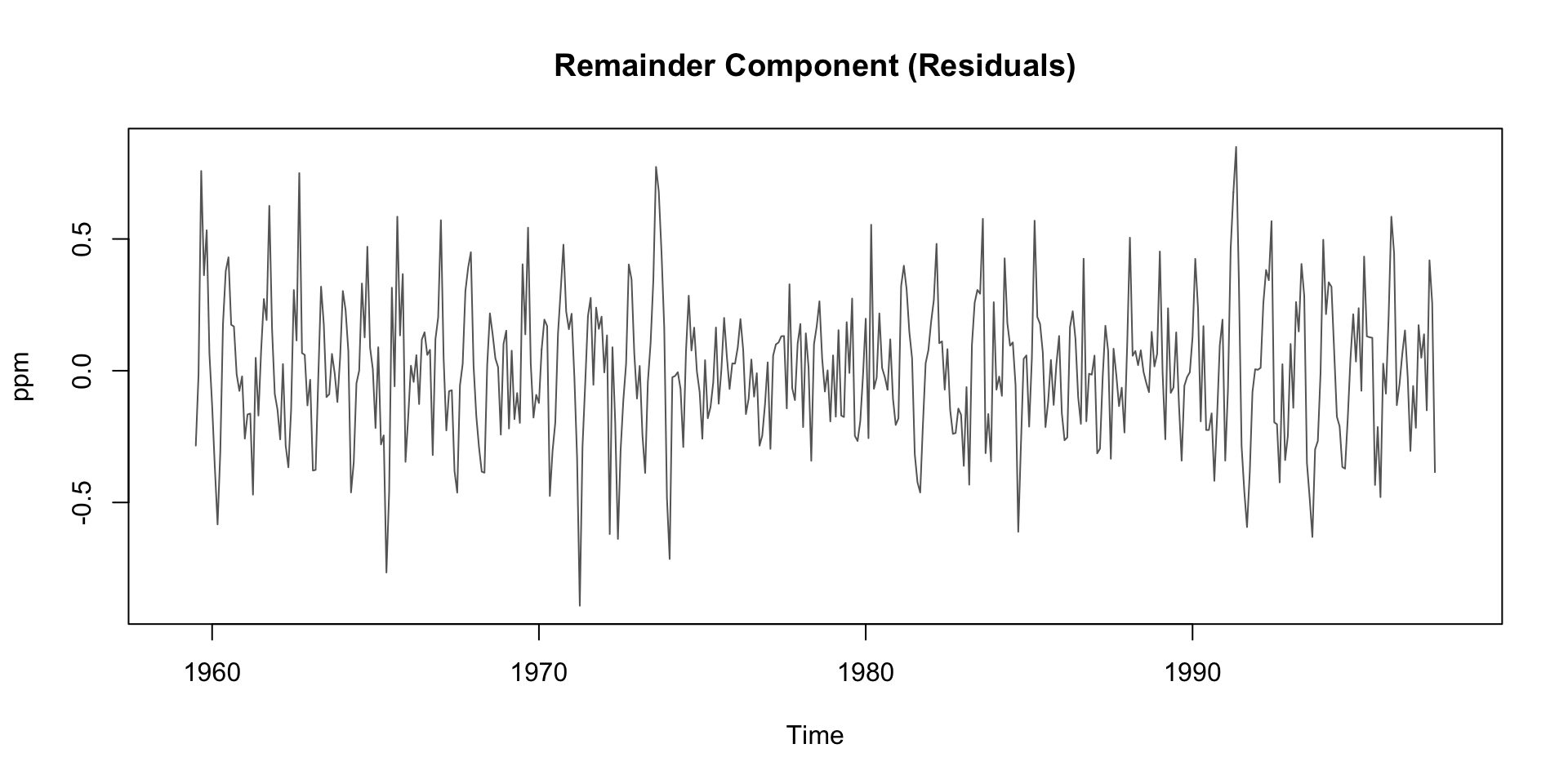
Deep Dive: Remainder Component
Residuals are the “leftover” part of the time series after removing trend and seasonality
Contains irregular, short-term fluctuations
Can be used to identify anomalies or outliers
Important for understanding noise in the data
Possible sources:
- Volcanic activity (e.g. El Chichón, Mt. Pinatubo)
- Measurement error
- El Niño/La Niña events (which affect carbon flux)
Typically small amplitude: ±0.2 ppm
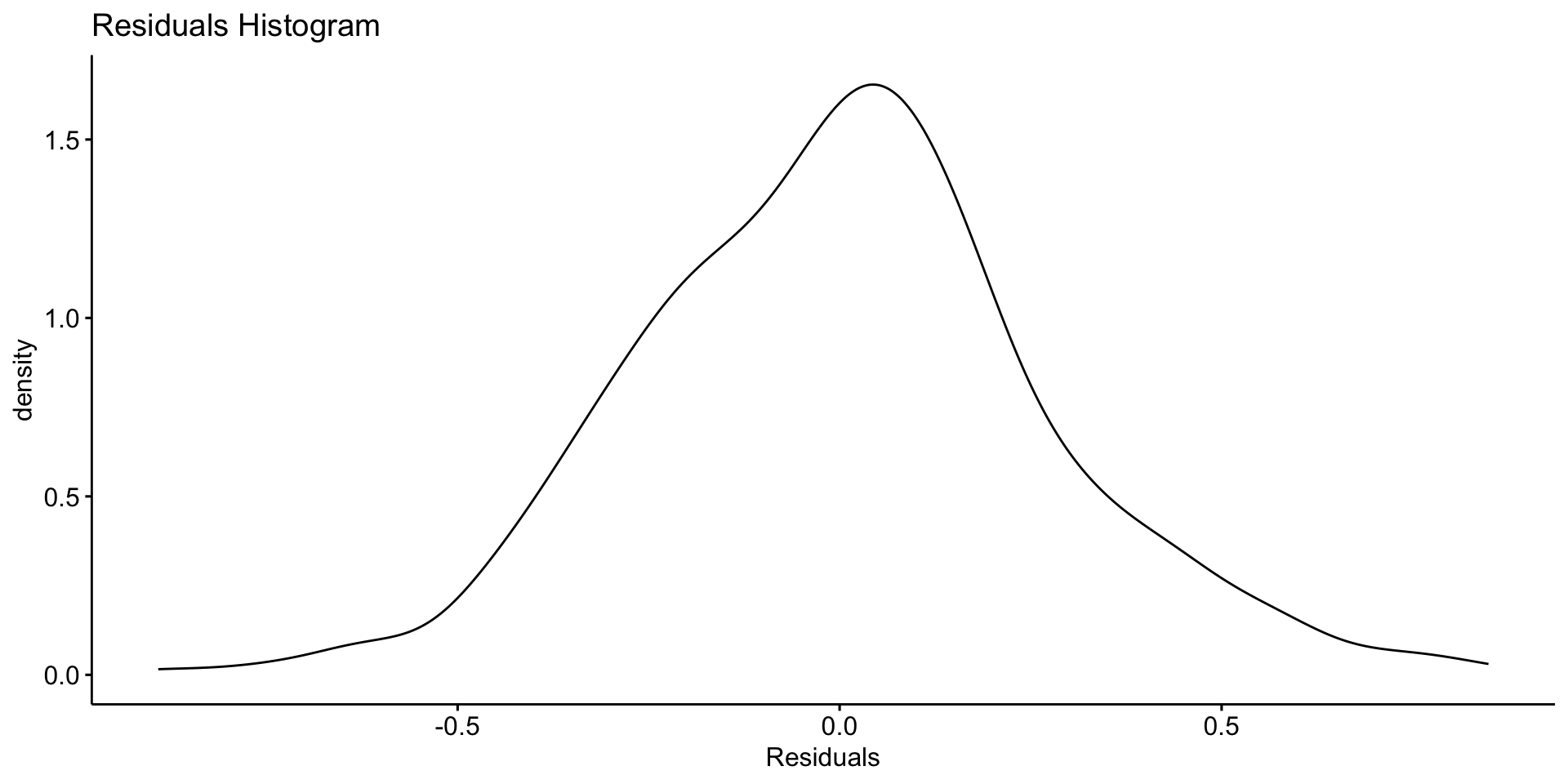
Asssessing Patterns in Error?
You might compute the standard deviation of the residuals to assess noise:
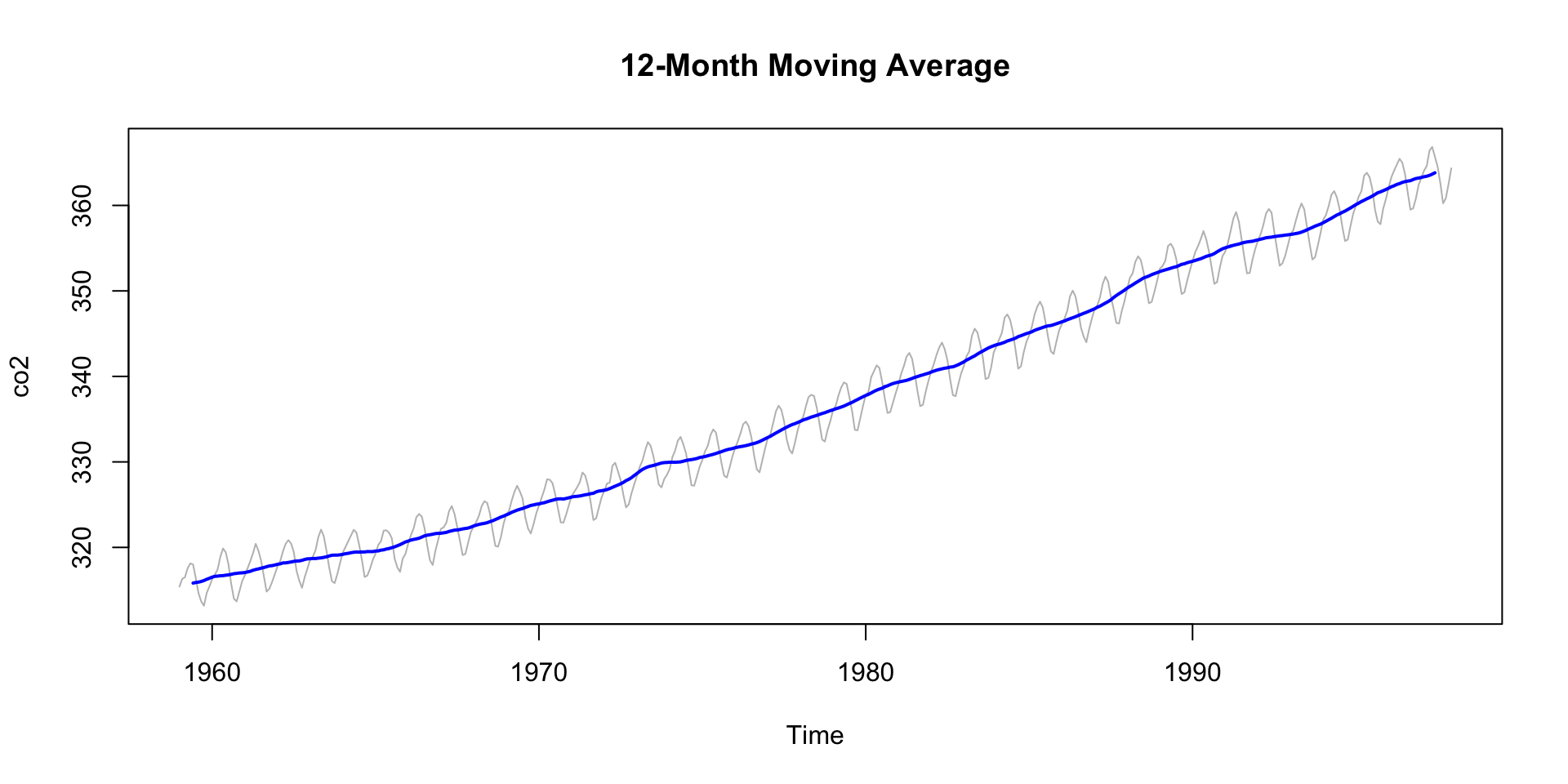
Smoothing to Remove Noise
If your data is noisy - and without usefull pattern - you can use a moving average to smooth it out.
- The
zoopackage provides a convenient function for this that we have already seen in the COVID lab. - The
rollmean()function from thezoopackage is useful for this. - The
kparameter specifies the window size for the moving average. - The
alignparameter specifies how to align the moving average with the original data (e.g., “center”, “left”, “right”). - The
na.padparameter specifies whether to pad the result withNAvalues.
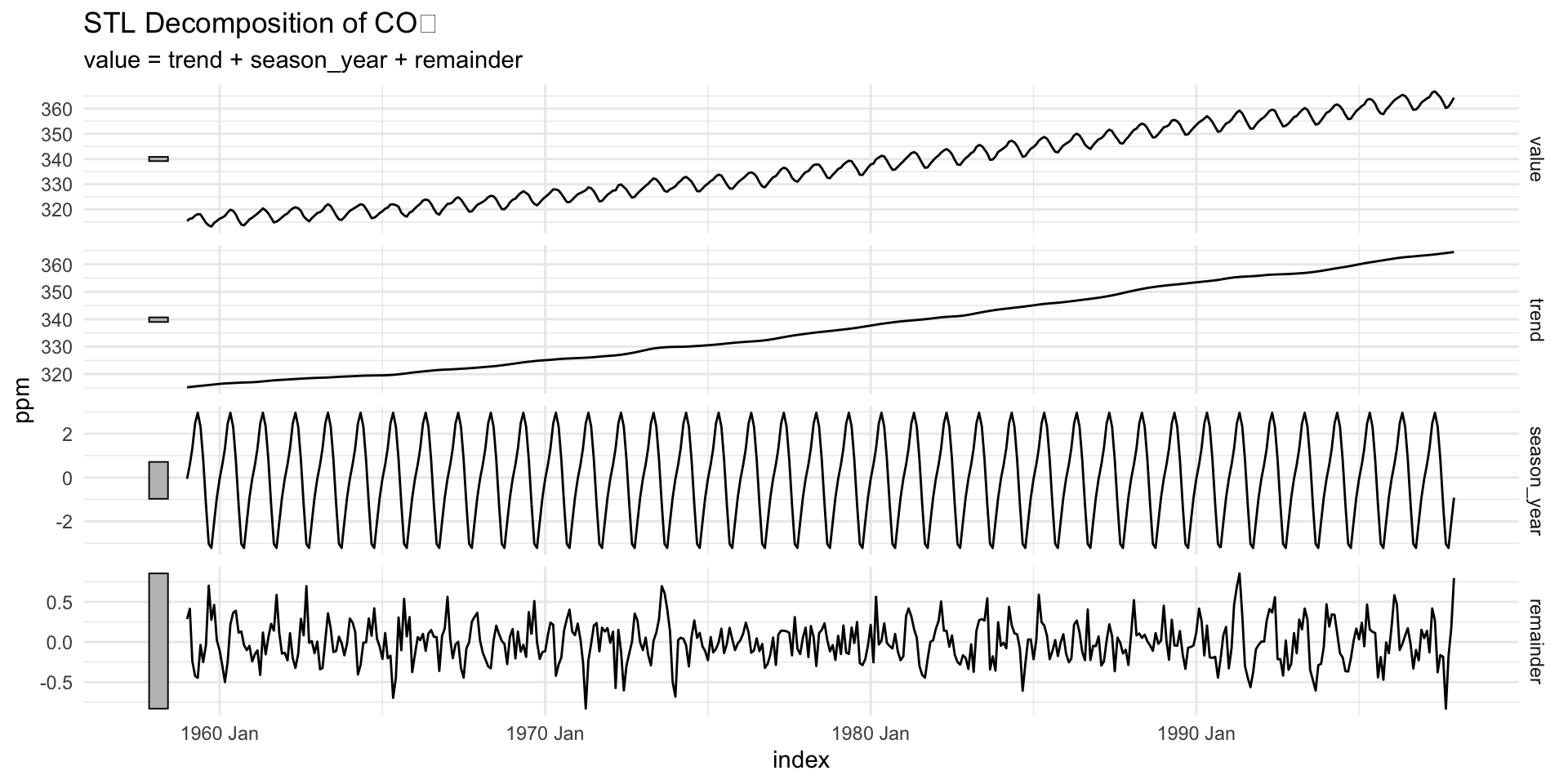
STL Decomposition (Loess-based)
STL (Seasonal-Trend decomposition using Loess) adapts to changing trend or seasonality over time
Doesn’t assume constant seasonal effect like
decompose()doesParticularly valuable when working with:
- Long datasets
- Environmental time series affected by nonlinear changes
STL Decomposition (Loess-based)
stl()uses local regression (loess) to estimate the trend and seasonal components.s.window = "periodic"specifies that the seasonal component is periodic.Other options include
- “none” (no seasonal component)
- or a numeric value for the seasonal window size.
Comparing Classical vs STL
| Method | Assumes Constant Season? | Robust to Outliers? | Adaptive Smoothing? |
|---|---|---|---|
| decompose | ✅ Yes | ❌ No | ❌ No |
| stl | ✅ or 🔄 (customizable) | ✅ Yes | ✅ Yes |
Recommendation: Use stl() for most real-world environmental time series.
Bringing It All Together
For the CO2 dataset, we can summarize the components of the time series:
- Trend: A human fingerprint — atmospheric CO₂ continues to rise year over year
- Seasonality: Driven by biospheric rhythms with not multiplicative gains
- Remainder: Small, but potentially rich with short-term signals
Understanding these components lets us:
✅ Track long-term progress
✅ Forecast future CO₂
✅ Communicate patterns clearly to policymakers
Time Series in the Tidyverse: tsibble / feasts
tsibbleis a tidy data frame for time series data. It extends the tibble class to include time series attributes.Compatible with
dplyr,ggplot2feastsprovides functions for time series analysis and visualization.
Decomposing with feasts
feasts provides:
- a
STL()function for seasonal decomposition. components()extracts the components of the decomposition.gg_season()andgg_subseries()visualize seasonal patterns.gg_lag()visualizes autocorrelation and lagged relationships.
co2_decomp <- co2_tbl |>
model(STL(value ~ season(window = "periodic"))) |>
components()
glimpse(co2_decomp)
#> Rows: 468
#> Columns: 7
#> Key: .model [1]
#> : value = trend + season_year + remainder
#> $ .model <chr> "STL(value ~ season(window = \"periodic\"))", "STL(value…
#> $ index <mth> 1959 Jan, 1959 Feb, 1959 Mar, 1959 Apr, 1959 May, 1959 J…
#> $ value <dbl> 315.42, 316.31, 316.50, 317.56, 318.13, 318.00, 316.39, …
#> $ trend <dbl> 315.1954, 315.3023, 315.4093, 315.5147, 315.6201, 315.71…
#> $ season_year <dbl> -0.06100103, 0.59463870, 1.32899651, 2.46904706, 2.95704…
#> $ remainder <dbl> 0.28564410, 0.41305456, -0.23825306, -0.42371128, -0.447…
#> $ season_adjust <dbl> 315.4810, 315.7154, 315.1710, 315.0910, 315.1730, 315.68…Component Access
Autoplot
Advanced Visualization/Modeling with feasts
gg_lag()
A lag plot is a scatterplot of a time series against itself, but with a time shift (or “lag”) applied to one of the series.
It helps us visualize the relationship between current and past values of a time series.
📦 Here’s the simple idea:
You take your CO₂ measurements over time.
Then you make a graph where you plot today’s CO₂ (on the Y-axis)…
…against CO₂ from a few months ago (on the X-axis).
This shows you if the past helps predict the present!
📊 If it makes a curvy shape or a line…
…that means there’s a pattern! Your data remembers what happened before — like a smart friend who learns from their past.
But if the dots look like a big messy spaghetti mess that means the data is random, with no memory of what happened before.
gg_lag()
🧠 Why this is useful:
It helps us see if there are patterns in the data.
It helps us understand how past values affect current values.
It helps us decide if we can use this data to make predictions in the future.
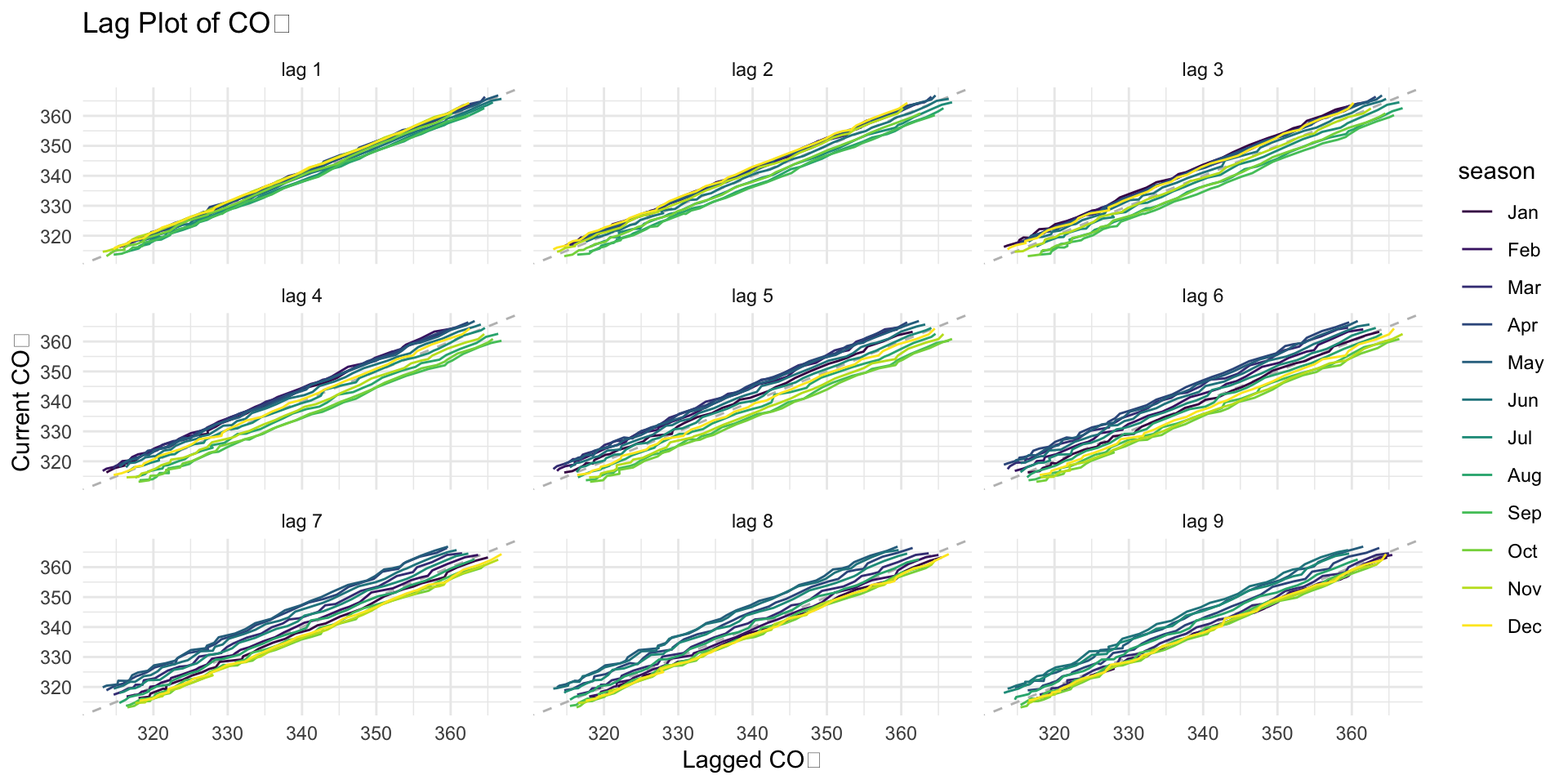
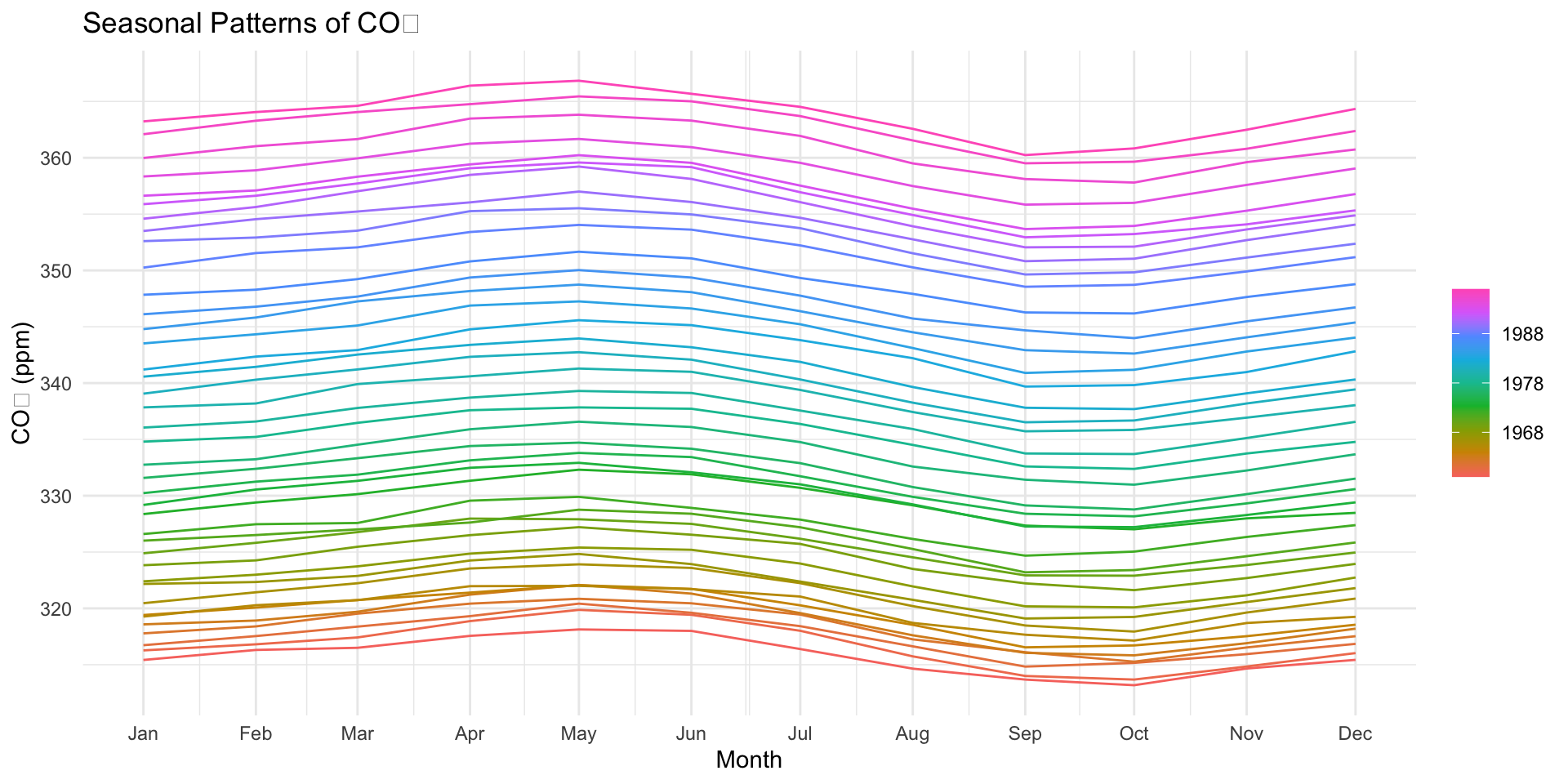
gg_subseries
Imagine the co2 dataset as a big collection of monthly CO₂ data from Mauna Loa. Each month is a group, and each year is a new object
Now, we want to see how each month behaves across the years, so we can spot if January always has higher or lower CO₂ levels, for example.
📊 What this does:
Each month: A different color shows up for each month (like January in blue, February in red, etc.)
Lines: You see the CO₂ values for each month over different years. For example, you might notice that CO₂ levels tend to be higher in the spring and lower in the fall.
🧠 Why this is useful:
We can spot seasonal trends: Does CO₂ rise in the winter? Or fall in the summer?
We can also compare months across the years: Is January more or less CO₂-heavy compared to other months?
gg_subseries()
gg_season
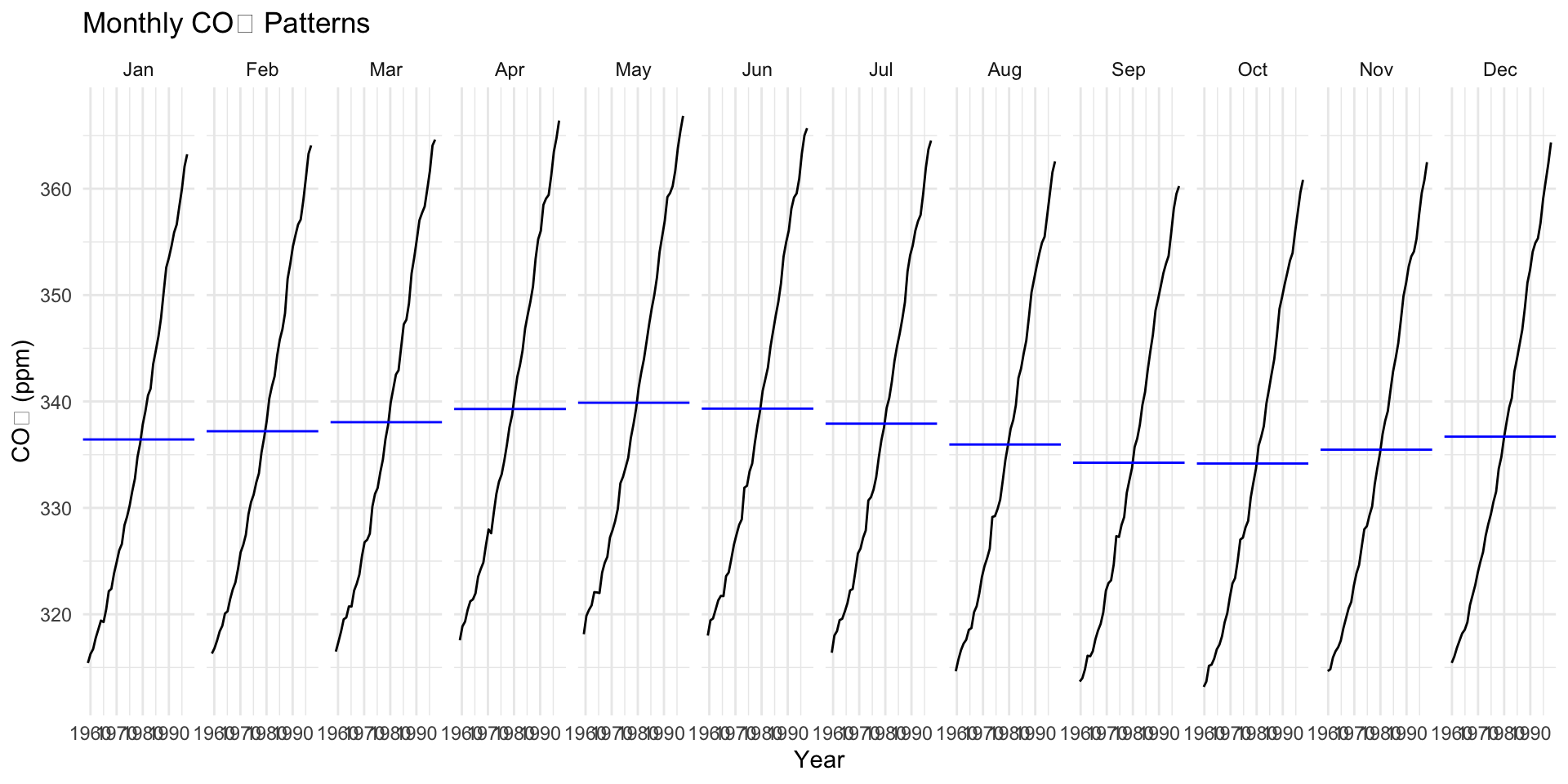
Think of
gg_season()like a way to look at a yearly picture of CO₂ and see if the Earth follows a seasonal rhythm.It makes the changes in CO₂ easy to spot when you look at months side-by-side.
📊 What this does:
- It shows you how CO₂ changes during each month of the year, but it puts all the years together, so you can see if the same thing happens every year in January, February, and so on.
🧠 Why this is useful:
- You’ll see a smooth curve for each month. Each curve shows how CO₂ goes up and down each year in the same pattern.
gg_season
Bonus: Interactive Plotting
In last weeks demo, we used plotly to generate an interactive plot of the hyperparameter tuning process.
You can use the
plotlypackage to add interactivity to your ggplots directly withggplotly()!
Bonus: Interactive Plotting
Forecasting:
- Forecasting with two distinct models (1) ARIMA (2) Prophet
- Understanding modeltime + tidymodels integration
- Forecasting Process for time series
Toy Example: River Time Series & ARIMA
Let’s say we’re watching how much water flows in a river every day:
- Monday: 50 cfs
- Tuesday: 60 cfs
- Wednesday: 70 cfs
We want to guess tomorrow’s flow.
1. AutoRegressive (AR)
This means: “Look at yesterday and the day before!”
If flow has been going up each day, AR says: ** “Tomorrow might go up again …” **
It’s like the river has a pattern.
2. Integrated (I)
Sometimes the flow just keeps climbing — like during a spring snowmelt!
To help ARIMA think better, we subtract yesterday’s number from today’s.
This makes the numbers more steady so ARIMA can do its magic.
3. Moving Average (MA)
The river sometimes gets a surprise flux (like a big rainstorm 🌧️).
MA looks at those surprises and helps smooth them out.
So if it rained two days ago, MA might say: “Don’t expect another surprise tomorrow.”
Put It All Together: AR + I + MA = ARIMA
- AR: Uses the river’s memory (trend)
- I: Calms the sturcutral components (season)
- MA: Handles noisy surprises (noise)
Now we can forecast tomorrow’s flow!
ARIMA
The basics of a ARIMA (AutoRegressive Integrated Moving Average) Model include:
- AR: AutoRegressive part (past values):
- AR(1) = current value depends on the previous value
- AR(2) = current value depends on the previous two values
- AR(1) = current value depends on the previous value
- I: Integrated part (differencing to make data stationary)
- Differencing removes trends and seasonality
- e.g.,
diff(co2, lag = 12)removes annual seasonality
- Differencing removes trends and seasonality
- MA: Moving Average part (past errors)
- MA(1) = current value depends on the previous error
- MA(2) = current value depends on the previous two errors
- MA(1) = current value depends on the previous error
- p, d, q: Parameters for AR, I, and MA
- p = number of lagged values (AR)
- d = number of differences (I)
- q = number of lagged errors (MA)
- p = number of lagged values (AR)
AIC
The AIC metric helps choose between models/parameters:
- It rewards:
- Good predictions
- Simplicity
- It punishes:
- Complexity (too many parameters)
- Overfitting (fitting noise instead of the trend)
- Lower AIC = better model
A Simple Forecasting Example
auto.arima()is a function from theforecastpackage that automatically selects the best ARIMA model for your data accoridning toe to the AICc criterion.- The AICc (Akaike Information Criterion corrected) is a measure of the relative quality of statistical models for a given dataset.
- It is used to compare different models and select the one that best fits the data while penalizing for complexity.
- The
auto.arima()function will automatically select the best parameters (p,d,q) based on the AICc criterion.
library(forecast)
co2_arima <- auto.arima(co2)
summary(co2_arima)
#> Series: co2
#> ARIMA(1,1,1)(1,1,2)[12]
#>
#> Coefficients:
#> ar1 ma1 sar1 sma1 sma2
#> 0.2569 -0.5847 -0.5489 -0.2620 -0.5123
#> s.e. 0.1406 0.1204 0.5880 0.5701 0.4819
#>
#> sigma^2 = 0.08576: log likelihood = -84.39
#> AIC=180.78 AICc=180.97 BIC=205.5
#>
#> Training set error measures:
#> ME RMSE MAE MPE MAPE MASE
#> Training set 0.01742092 0.287159 0.2303994 0.005073769 0.06845665 0.1819636
#> ACF1
#> Training set -0.002858162Forecasting with ARIMA
- The
forecast()function is used to generate forecasts from the fitted ARIMA model. - The
hargument specifies the number of periods to forecast into the future.
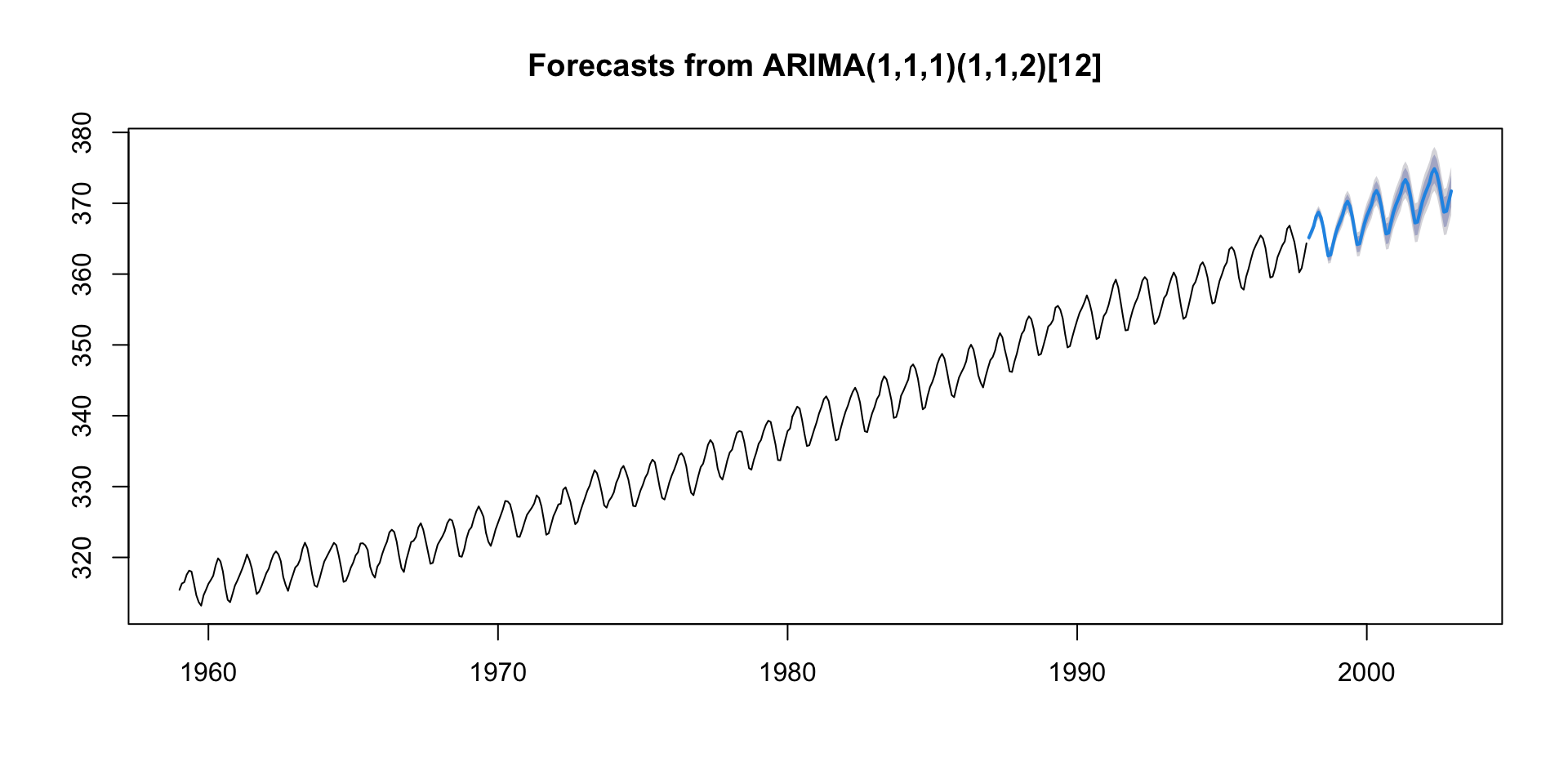
🔢 ARIMA(1,1,1)(1,1,2)[12]
ARIMA Notation can be broken into two parts:
1. Non-seasonal part: ARIMA(1, 1, 1)
This is the “regular” ARIMA: - AR(1): One autoregressive term — the model looks at one lag of the time series.
I(1): One differencing — the model uses the change in values instead of raw values to make the series more stationary.
MA(1): One moving average term — the model corrects using one lag of the error term.
2. Seasonal part: (1, 1, 2)[12]
This is the seasonal pattern — repeated every 12 time units (like months in a year):
SAR(1): One seasonal autoregressive term — it uses the value from 12 time steps ago.
SI(1): One seasonal difference — subtracts the value from 12 steps ago to remove seasonal patterns.
SMA(2): Two seasonal moving average terms — uses errors from 12 and 24 time steps ago.
[12]: This is the seasonal period, i.e., it’s a yearly pattern with monthly data.
🔢 ARIMA(1,1,1)(1,1,2)[12]
Hey, ARIMA please…
“Model the data using a mix of its last value, the last error, and their seasonal versions from 12 months ago — but first difference it once to remove trend and once seasonally to remove yearly patterns.”
Note
ARIMA modeling works well when data is stationary. - Stationarity means the statistical properties of the series (mean, variance) do not change over time. - Non-stationary data can lead to unreliable forecasts and misleading results.
Prophet
Prophet is an open-source tool for forecasting time series data.
Developed by Facebook (Meta)
Designed for analysts and data scientists
Handles missing data, outliers, and seasonality
Key Features of Prophet
✅ Additive Model: Trend + Seasonality + Holidays + Noise
✅ Automatic Changepoint Detection
✅ Support for Custom Holidays & Events
✅ Flexible Seasonality (daily/weekly/yearly)
✅ Easy-to-use API in R and Python
Prophet’s Model Structure
Prophet decomposes time series into components:
\[ y(t) = g(t) + s(t) + h(t) + ε(t) \]
g(t): Trend (linear or logistic growth)
s(t): Seasonality (Fourier series)
h(t): Holiday effects
ε(t): Error term (noise)
📌 Assumes additive components by default; multiplicative also possible
A Simple Forecasting Example
Your time series must have: (1) ds column (date/timestamp) (2) y column (value to forecast)
Pros / Cons
| Feature | ARIMA | Prophet |
|---|---|---|
| Statistical rigor | Based on strong statistical theory; well-studied | Intuitive, decomposable model (trend + seasonality + events) |
| Interpretability | Clear interpretation of AR, MA, differencing terms | Plots components like trend/seasonality directly |
| Flexibility (SARIMA) | Seasonal ARIMA can handle seasonal structure | Handles multiple seasonalities natively (yearly, weekly, daily) |
| Control over params | Fine-tuned control over differencing, lags, and model order | Easy to specify changepoints, seasonality, and custom events |
| Statistical testing | Includes AIC/BIC for model selection | Cross-validation support; uncertainty intervals included |
| Requires stationarity | Time series must be stationary or made so (differencing) | Handles non-stationary data out of the box |
| Model complexity | Needs careful tuning (p,d,q) and domain expertise | Defaults work well; limited tuning needed |
| Holiday effects | Must be encoded manually | Easy to include holidays/events |
| Multivariate support | Basic ARIMA doesn’t support exogenous variables easily (need ARIMAX) | Supports external regressors with add_regressor() |
| Non-linear trends | Poor performance with structural breaks or non-linear growth | Handles changepoints and logistic growth models well |
| Seasonality limits | SARIMA handles only one seasonal period well | Built-in multiple seasonal components (e.g., daily, weekly, yearly) |
TL;DR
- Use ARIMA if you want a classic, statistical model with deep customization and you’re comfortable making your data stationary.
- Use Prophet if you want a fast, robust, and intuitive model for business or environmental data with strong seasonal effects and irregular events.
To much complexity!!
Each model has it own requirements, arguments, and tuning parameters.
Simular to our ML models, this introduces a large time sink, opportunity for error, and complexity.
modeltimebrings tidy workflows to time series forecasting using theparsnipandworkflowsframeworks fromtidymodels.Combine multiple models (ARIMA, Prophet, XGBoost) in one framework to
Modeltime Integration ![]()
![]()
1. Create a time series split …
Use
time_series_split()to make a train/test set.Setting assess = “…” tells the function to use the last … of data as the testing set.
Setting cumulative =
TRUEtells the sampling to use all of the prior data as the training set.
2. Specify Models …
Just like tidymodels …
Model Spec:
arima_reg()/prophet_reg()/prophet_boost()<– This sets up your general model algorithm and key parametersModel Mode:
mode = "regression"/mode = "classification"<– This sets the model mode to regression or classification (timeseries is always regression!)Set Engine:
set_engine("auto_arima")/set_engine("prophet")/ <– This selects the specific package-function to use, you can add any function-level arguments here.
mods <- list(
arima_reg() |> set_engine("auto_arima"),
arima_boost(min_n = 2, learn_rate = 0.015) |> set_engine(engine = "auto_arima_xgboost"),
prophet_reg() |> set_engine("prophet"),
prophet_boost() |> set_engine("prophet_xgboost"),
# Exponential Smoothing State Space model
exp_smoothing() |> set_engine(engine = "ets"),
# Multivariate Adaptive Regression Spline model
mars(mode = "regression") |> set_engine("earth")
)3. Fit Models …
Use
purrr::map()tofitthemodelsto the training data.Fit Model: fit(value ~ date, training) <– All
modeltimemodels require a date column to be a regressor.
4. Build modeltime table …
- Use
modeltime_table()to combine multiple models into a single table that can be used for calibration, accuracy, and forecasting.
modeltime_table():
Creates a table of models
Validates that all objects are models (parsnip or workflows objects) and all models have been fitted
Provides an ID and Description of the models
as_modeltime_table():
- Converts a list of models to a modeltime table. Useful if programatically creating Modeltime Tables from models stored in a list (e.g. from
map).
(models_tbl <- as_modeltime_table(models))
#> # Modeltime Table
#> # A tibble: 6 × 3
#> .model_id .model .model_desc
#> <int> <list> <chr>
#> 1 1 <fit[+]> ARIMA(1,1,1)(2,1,2)[12]
#> 2 2 <fit[+]> ARIMA(1,1,1)(0,1,1)[12]
#> 3 3 <fit[+]> PROPHET
#> 4 4 <fit[+]> PROPHET
#> 5 5 <fit[+]> ETS(M,A,A)
#> 6 6 <fit[+]> EARTHNotes:
modeltime_table() does some basic checking to ensure all models are fit and organized into a scalable structure called a “Modeltime Table” that is used as part of our forecasting workflow.
- It’s expected that tuning and parameter selection is performed prior to incorporating into a Modeltime Table.
- If you try to add an unfitted model, the
modeltime_table()will complain (throw an informative error) saying you need to fit() the model.
5. Calibrate the Models …
Use
modeltime_calibrate()to evaluate the models on the test set.Calibrating adds a new column,
.calibration_data, with the test predictions and residuals inside.
(calibration_table <- modeltime_calibrate(models_tbl, testing, quiet = FALSE))
#> # Modeltime Table
#> # A tibble: 6 × 5
#> .model_id .model .model_desc .type .calibration_data
#> <int> <list> <chr> <chr> <list>
#> 1 1 <fit[+]> ARIMA(1,1,1)(2,1,2)[12] Test <tibble [60 × 4]>
#> 2 2 <fit[+]> ARIMA(1,1,1)(0,1,1)[12] Test <tibble [60 × 4]>
#> 3 3 <fit[+]> PROPHET Test <tibble [60 × 4]>
#> 4 4 <fit[+]> PROPHET Test <tibble [60 × 4]>
#> 5 5 <fit[+]> ETS(M,A,A) Test <tibble [60 × 4]>
#> 6 6 <fit[+]> EARTH Test <tibble [60 × 4]>A few notes on Calibration:
Calibration builds confidence intervals and accuracy metrics
Calibration Data is the predictions and residuals that are calculated from out-of-sample data.
After calibrating, the calibration data follows the data through the forecasting workflow.
Testing Forecast & Accuracy Evaluation
There are 2 critical parts to an evaluation.
- Evaluating the Test (Out of Sample) Accuracy
- Visualizing the Forecast vs Test Data Set
Accuracy
modeltime_accuracy() collects common accuracy metrics using yardstick functions:
- MAE - Mean absolute error, mae()
- MAPE - Mean absolute percentage error, mape()
- MASE - Mean absolute scaled error, mase()
- SMAPE - Symmetric mean absolute percentage error, smape()
- RMSE - Root mean squared error, rmse()
- RSQ - R-squared, rsq()
modeltime_accuracy(calibration_table) |>
arrange(mae)
#> # A tibble: 6 × 9
#> .model_id .model_desc .type mae mape mase smape rmse rsq
#> <int> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 ARIMA(1,1,1)(2,1,2)[12] Test 0.810 0.224 0.687 0.224 0.967 0.973
#> 2 2 ARIMA(1,1,1)(0,1,1)[12] Test 0.885 0.244 0.750 0.245 1.05 0.969
#> 3 3 PROPHET Test 1.06 0.295 0.899 0.294 1.16 0.986
#> 4 4 PROPHET Test 1.06 0.295 0.899 0.294 1.16 0.986
#> 5 5 ETS(M,A,A) Test 1.48 0.409 1.25 0.410 1.71 0.958
#> 6 6 EARTH Test 1.89 0.526 1.61 0.526 2.25 0.499Forecast
- Use
modeltime_forecast()to generate forecasts for the next 120 months (10 years). - Use
plot_modeltime_forecast()to visualize the forecasts.
(forecast <- calibration_table |>
modeltime_forecast(h = "60 months",
new_data = testing,
actual_data = co2_tbl) )
#> # Forecast Results
#>
#> # A tibble: 828 × 7
#> .model_id .model_desc .key .index .value .conf_lo .conf_hi
#> <int> <chr> <fct> <date> <dbl> <dbl> <dbl>
#> 1 NA ACTUAL actual 1959-01-01 315. NA NA
#> 2 NA ACTUAL actual 1959-02-01 316. NA NA
#> 3 NA ACTUAL actual 1959-03-01 316. NA NA
#> 4 NA ACTUAL actual 1959-04-01 318. NA NA
#> 5 NA ACTUAL actual 1959-05-01 318. NA NA
#> 6 NA ACTUAL actual 1959-06-01 318 NA NA
#> 7 NA ACTUAL actual 1959-07-01 316. NA NA
#> 8 NA ACTUAL actual 1959-08-01 315. NA NA
#> 9 NA ACTUAL actual 1959-09-01 314. NA NA
#> 10 NA ACTUAL actual 1959-10-01 313. NA NA
#> # ℹ 818 more rowsVizualize
Refit to Full Dataset & Forecast Forward
The final step is to refit the models to the full dataset using modeltime_refit() and forecast them forward.
Why refit?
The models have all changed! This is the (potential) benefit of refitting.
More often than not refitting is a good idea. Refitting:
Retrieves your model and preprocessing steps
Refits the model to the new data
Recalculates any automations. This includes:
- Recalculating the changepoints for the Earth Model
- Recalculating the ARIMA and ETS parameters
Preserves any parameter selections. This includes:
Any other defaults that are not automatic calculations are used.
Growing Ecosystem
Summary & Takeaways
Environmental science is rich with time series applications
Time series data is sequential and ordered
lubridatesimplifies handling and extracting date-time featuresUse
ts,zoo,xtsfor classic or irregular dataUse
tsibble,feasts, andfablefor tidy workflowsLearn to decompose, smooth, and forecast
Use
modeltimefor advanced modeling and forecasting